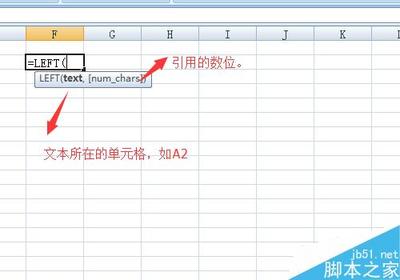
在物理学中,场是一个十分重要的概念。场可以分为矢量场和标量场。由于在研究宏观场时,矢量场的测量不如标量场来的直接,因此常常测量对应的标量场来间接地测量矢量场。比如一个无旋场首先测量空间各点的电势,通过对电势求梯度从而得到电场。在研究平面场时,往往还需要用到所谓的流函数。
如果场源是点源,比如点电荷,则场线会向三维空间的每个方向发散。而有一类矢量场中的矢量都平行于某个平面S,而且在垂直于S的任何一条直线上的所有点处的矢量都是相等的;场中的矢量也都是与时间无关的。显然,这种向量场在所有平行于S的平面内的分布情况是完全相同的,因此它完全可以用一个位于平行于S的平面S0内的场来表示。这样的场称为平面场,如图1所示。
图1
比如无限大平行板电容器,两极板上有均匀分布的等量异性电荷,则极板间的电场只有一个方向;再比如无限长细直导线上有直流电流I,则根据右手定则导线周围磁场有围绕导线的磁场,但该磁场没有z方向的分量(实际上z方向上的分量相互抵消了),如图2所示

图2
根据麦克斯韦方程有
(1)
说明远离导线的地方磁场强度比较小,而靠近导线的地方磁场强度比较大。于是我们要测量远离导线的时候这个磁场强度的减小趋势。由于对称性的关系,我们放入一个小指南针,从导线附近,沿着辐线直线移动,发现磁场对指南针不做功。因为磁力和指南针的运动方向正交,也就是说xOy平面中,任何一条从细导线所在点发出的射线都是磁场的等势线。这样势函数就无法完全确定场的分布。
从而需要引入一个流函数的概念。流函数具有这样的物理意义:
平面流动中,通过两条流线间任一曲线单位厚度的体积流量等于两条流线的流函数之差。
图3
直观地说,如图2中一个人站立于xOy平面上,从一定点a出发,沿曲线段到达b点,这个过程中人从头到脚切割磁感线,切割从右手穿过的磁感线的数目减掉所切割的从左手穿过的磁感线,剩下的所切割的磁感线的数目(即净数目或净流量)乘以人的身高(单位长度)就等于a点与b点之间的流函数之差。如果行走的是某点处很小的闭合路径,从而确定一个体积元dV,此时流函数之差除以dV有散度的物理意义。
在描绘一个平面流速场时,往往是画出它的等势线和等流线。如图4所示。
图4
两个等量异性点电荷形成的电场。虚线为等势线,实线为流线(后面将揭示流线方向和电场线方向相同,两个点电荷显然不会形成平面场,但平面场等势线和流线与之类似)等势线和流线处处正交。
基于上面的结论,那么我们就需要两个函数来描述一个矢量场,从而分别画出等势线和等流线。
前面说某点处流函数之差除以dV有散度的物理意义,所以要找出等流线就意味着找出满足下列方程的点的集合
(2)
其中ψ为流函数。而对于一个矢量有散度公式
在平面场中,z方向的分量不存在,在z方向求偏导数也无意义,于是改写散度公式(这里令F=iu(x,y)+jv(x,y))
(3)从而有
(4)
如果前面所说的人在xOy平面上行走的路径是构成一个单连通区域,则会确定一个柱形区域,如图5所示。
图5
如果这个区域中没有散度源,则(4)式两边积分有
(5)
从而根据格林公式(Green'sTheorem)有
(6)
从而可知,如果定义域内没有散度源,则流函数与路径无关。且使图5所示的闭合曲线按极限缩小为一点,则有全微分
故
(7)
所以从流函数可以得到平面场。而对于等流线ψ=C(C为常数)的任意点处有切矢量i+jdy/dx=i+jv/u=ui+vj。所以说等流线各点处的切矢量方向就是对应的矢量场的方向。
接下来讨论势函数。如果矢量场在某区域内是有势场,则该区域内不存在漩涡源,即该区域内的任意一点处旋度为0。对于空间一矢量,有旋度公式
(8)
关于前面所说的平面场F=ui+vj,旋度为
(9)
如果区域内没有漩涡源,则势函数之差与路径无关。也就是说当这样的势场内一点沿闭合路径运动一周,势函数之差为0。若闭合曲线为∂D+,其包围的平面为Dxy。与(5)式类似地有
(10)
当闭合曲线收缩于一点时,则势函数的全微分为
(11)
故
(12)
实际上求势函数的梯度就得到对应的矢量场
(13)
而等势线有切矢量i+jdy/dx=i+ju/v=vi+uj。所以等势线与对应的矢量场处处正交。
以上的讨论中发现为了表示一个空间中无散无旋的平面矢量场,需要用到势函数和流函数,这就需要两个方程。能否用一个方程同时表示势函数和流函数?并且分析上面势函数和流函数的关系,能否当两者之一确定时,同时确定另外一个?
这是就要借助于复变函数的理论。在“复变函数论”中,解析函数有重要的意义。复变函数f(z)=u(x,y)+iv(x,y)在其定义域D内解析的充要条件是:u(x,y)与v(x,y)在D内可微,并且满足柯西-黎曼方程(Cauchy-Rieman'sEquation)
(14)
关于这个定理的证明参见各种复变函数教程。根据复数的几何意义,如果有一个在平面D内连续且无旋无散的平面矢量场F=ui+vj,则可用D对应的复平面D'内的一个解析函数来表示:F=u+iv,它满足柯西-黎曼方程。
而该矢量场对应着一个复势函数,它的实部为前面所提到的势函数,而虚部为流函数。
(15)
有求导公式
(16)
结合(7)式和(12)式有
(17)
字母F头上的一横表示取其共轭复数。实际上柯西-黎曼方程的几何意义是解析函数在其定义区间内的曲线积分与路径无关。复平面上的一条曲线l,可以发现dl=dz=dx+idy,从而有
(18)
接下来求图2所示的平面磁场的复势,并画出等势线和等流线。假设细导线位于复平面上的原点,载有大小为I的直流电流,如图6所示。则根据毕奥-萨伐尔定律(Biot-SavartLaw)有
而R=r/sinα,l=r/tanα,所以dl=-(r/sin2α)dα,则上式变为
(19)
这也验证了(1)式,又因为单位矢量eθ在复平面上可表示为
图6
所以(19)式用复数形式表示为
(20)
这是一个除了原点之外处处解析的复变函数(无旋无散)。那么设平面磁场B的复势为f(z)=φ+iψ,有
显然流函数的容易求得
(21)
其中C1为一常数,而势函数的求法先上下两边同除以x2有
从而有
(22)
其中C2也为一常数。可以画出如图7所示的平面场示意图
图7
从流函数可以看出,等流线是一个个同心圆,在原点处没有意义,是一个奇点。而等势线是从原点出发的射线,在原点也同样没有意义。这里有趣的是,如果场中一点运行的路径不是闭合的,则考虑其运动路径所在的局部场还是一个保守场(有势场),比如发电机最终与负载构成回路,环路是包围漩涡源的,但是当只分析负载电路,不考虑电源内部情况时,还是认为电源提供的是一个有势电场。
 爱华网
爱华网