转载:用于学习参考,望原文作者海涵!
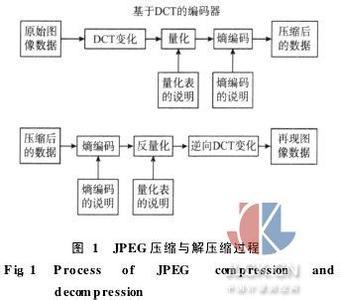
数据压缩技术的理论基础是信息论。根据信息论的原理,可以找到最佳数据压缩编码方法,数据压缩的理论极限是信息熵。如果要求在编码过程中不丢失信息量,即要求保存信息熵,这种信息保持编码又叫做熵保存编码,或者叫熵编码。
熵编码是无失真数据压缩,用这种编码结果经解码后可无失真地恢复出原图像。当考虑到人眼对失真不易觉察的生理特征时,有些图像编码不严格要求熵保存,信息可允许部分损失以换取高的数据压缩比,这种编码是有失真数据压缩,通常运动图像的数据压缩是有失真编码。
JPEG压缩算法使用了两种熵编码方法:哈夫曼编码和算术编码。在此我们只介绍哈夫曼编码。哈夫曼编码Huffman方法于1952年问世,迄今为止仍经久不衰,广泛应用于各种数据压缩技术中,且仍不失为熵编码中的最佳编码方法。
哈夫曼编码的理论依据是变字长编码理论。在变字长编码中,编码器的编码输出码字是字长不等的码字,按编码输入信息符号出现的统计概率,给输出码字分配以不同的字长。对于编码输入中,出现大概率的信息符号,赋以短字长的输出码字;
对于编码输入中,出现小概率的信息符号,赋以长字长的输出码字。可以证明,按照概率出现大小的顺序,对输出码字分配不同码字长度的变字长编码方法,其输出码字的平均码长最短,与信源熵值最接近,编码方法最佳。
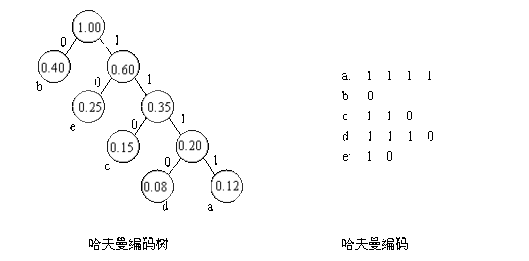
哈夫曼编码的具体步骤归纳如下:
①概率统计(如对一幅图像,或m幅同种类型图像作灰度信号统计),得到n个不同概率的信息符号。
②将n个信源信息符号的n个概率,按概率大小排序。
③将n个概率中,最后两个小概率相加,这时概率个数减为n-1个。
④将n-1个概率,按大小重新排序。
⑤重复③,将新排序后的最后两个小概率再相加,相加和与其余概率再排序。
⑥如此反复重复n-2次,得到只剩两个概率序列。
⑦以二进制码元(0.1)赋值,构成哈夫曼码字。编码结束。
哈夫曼码字长度和信息符号出现概率大小次序正好相反,即大概信息符号分配码字长度短,小概率信息符号分配码字长度长。
哈夫曼树定义为:给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffmantree)。
1、那么什么是权值?什么是路径长度?什么是带权路径长度呢?
权值:哈夫曼树的权值是自己定义的,他的物理意义表示数据出现的次数、频率。可以用树的每个结点数据域data存放一个特定的数表示它的值。
路径长度:在一棵树中,从一个结点往下可以达到的孩子或子孙结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。树中所有叶子节点的带权路径长度之和,WPL=sigma(w*l)
2、哈夫曼树的构造过程。(结合图例)
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:
(1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);
(2)在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树加入森林;
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树
3、哈夫曼树的应用:哈夫曼编码(前缀编码)
哈夫曼编码
在数据通信中,通常需要把要传送的文字转换为由二进制字符0和1组成的二进制串,这个过程被称之为编码(Encoding)。例如,假设要传送的电文为DCBBADD,电文中只有A、B、C、D四种字符,若这四个字符采用表(a)所示的编码方案,则电文的代码为11100101001111,代码总长度为14。若采用表(b) 所示的编码方案,则电文的代码为0110101011100,代码总长度为13。
字符集的不同编码方案
哈夫曼树可用于构造总长度最短的编码方案。具体构造方法如下:
设需要编码的字符集为{d1,d2,…,dn},各个字符在电文中出现的次数或频率集合为{w1,w2,…,wn}。以d1,d2,…,dn作为叶子结点,以w1,w2,…,wn作为相应叶子结点的权值来构造一棵哈夫曼树。规定哈夫曼树中的左分支代表0,右分支代表1,则从根结点到叶子结点所经过的路径分支组成的0和1的序列便为该结点对应字符的编码就是哈夫曼编码(Huffman Encoding)。
在建立不等长编码中,必须使任何一个字符的编码都不是另一个编码的前缀,这样才能保证译码的唯一性。例如,若字符A的编码是00,字符B的编码是001,那么字符A的编码就成了字符B的编码的后缀。这样,对于代码串001001,在译码时就无法判定是将前两位码00译成字符A还是将前三位码001译成B。这样的编码被称之为具有二义性的编码,二义性编码是不唯一的。而在哈夫曼树中,每个字符结点都是叶子结点,它们不可能在根结点到其它字符结点的路径上,所以一个字符的哈夫曼编码不可能是另一个字符的哈夫曼编码的前缀,从而保证了译码的非二义性。
下图就是电文DCBBADD的哈夫曼树:
4、哈夫曼树的实现
由哈夫曼树的构造算法可知,用一个数组存放原来的n个叶子结点和构造过程中临时生成的结点,数组的大小为2n-1。所以,哈夫曼树类HuffmanTree中有两个成员字段:data数组用于存放结点,leafNum表示哈夫曼树叶子结点的数目。结点有四个域,一个域weight,用于存放该结点的权值;一个域lChild,用于存放该结点的左孩子结点在数组中的序号;一个域rChild,用于存放该结点的右孩子结点在数组中的序号;一个域parent,用于判定该结点是否已加入哈夫曼树中。
哈夫曼树结点的结构为:| 数据 | weight | lChild | rChild | parent |
public class Node
{
char c; //存储的数据,为一个字符
private double weight; //结点权值
private int lChild; //左孩子结点
private int rChild; //右孩子结点
private int parent; //父结点
//结点权值属性
public double Weight
{
get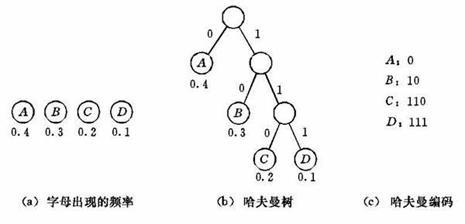
{
return weight;
}
set
{
weight = value;
}
}
//左孩子结点属性
public int LChild
{
get
{
return lChild;
}
set
{
lChild = value;
}
}
//右孩子结点属性
public int RChild
{
get
{
return rChild;
}
set
{
rChild = value;
}
}
//父结点属性
public int Parent
{
get
{
return parent;
}
set
{
parent = value;
}
}
//构造器
public Node()
{
weight = 0;
lChild = -1;
rChild = -1;
parent = -1;
}
//构造器
public Node(double weitht)
{
this.weight = weitht;
lChild = -1;
rChild = -1;
parent = -1;
}
//构造器
public Node(int w, int lc, int rc, int p)
{
weight = w;
lChild = lc;
rChild = rc;
parent = p;
}
}
publicclass HuffmanTree
{
private Node[] data; //结点数组
private int leafNum; //叶子结点数目
//索引器
public Node this[int index]
{
get
{
return data[index];
}
set
{
data[index] = value;
}
}
//叶子结点数目属性
public int LeafNum
{
get
{
return leafNum;
}
set
{
leafNum = value;
}
}
//构造器
public HuffmanTree(int n)
{
data = new Node[2 * n - 1];
leafNum = n;
}
//创建哈夫曼树
public void Create(Node[] datain)
{
double minL, minR;
minL = minR = double.MaxValue;
int lchild, rchild;
lchild = rchild = -1;
int length = data.Length;
//初始化哈夫曼树
for (int i = 0; i < length; i++)
data[i] = new Node();
for (int i = 0; i < datain.Length; i++)
data[i] = datain[i];
//处理n个叶子结点,建立哈夫曼树
for (int i = leafNum; i < length; i++)
{
//在全部结点中找权值最小的两个结点
for (int j = 0; j < i; j++)
{
if (data[j].Parent == -1)
{
if (data[j].Weight < minL)
{
minR = minL;
minL = data[j].Weight;
rchild = lchild;
lchild = j;
}
else if (data[j].Weight < minR)
{
minR = data[j].Weight;
rchild = j;
}
}
}
data[lchild].Parent = data[rchild].Parent = i;
data[i].Weight = minL + minR;
data[i].LChild = lchild;
data[i].RChild = rchild;
}
}
}
classProgram
{
static void Main(string[] args)
{
HuffmanTree tree = new HuffmanTree(5);
Node[] nodes = new Node[] { new Node(1), new Node(2), newNode(2.5d), new Node(3), new Node(2.6d) };
tree.Create(nodes);
Console.ReadLine();
}
}
/////////////////////////////节选自网络上的资料、
 爱华网
爱华网