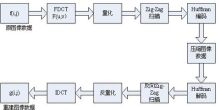
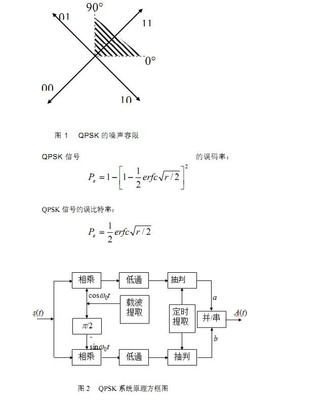
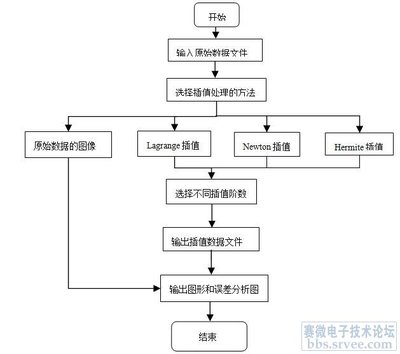
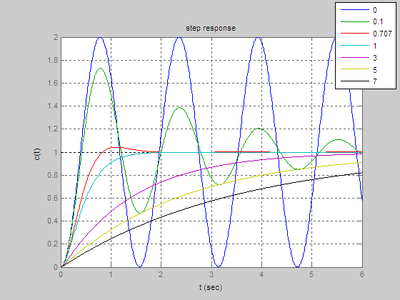
解:周期为T0的矩形信号可以表示
其傅里叶级数系数为
由于矩形信号串x(t)为实值周期函数,且为偶函数,所以傅里叶级数系数xn为实数。由此得到三角函数形式的傅里叶级数展开的系数为
周期信号的三角函数形式的傅里叶展开为
下面图所示,给出了T1=T0/2=2的离散幅度谱。通过n=1,…,9次谐波叠加后的波形可以看出,随着展开次数的增加,近似的波形将愈加接近原信号。

====================================================================
程序清单:
% 2014-8-25 rectexpd.m
% 矩形信号串---信号分解与合成
% T1:矩形信号区间为(-T1/2,T1/2)
% T0: 矩形信号串周期
% m: 傅里叶级数展开项次数
T1=2;T0=4;m=9;
t1=-T1/2:0.01:T1/2;
t2=T1/2:0.01:(T0-T1/2);
t=[(t1-T0)';(t2-T0)';t1';t2';(t1+T0)'];
n1=length(t1);
n2=length(t2); % 根据周期矩形信号函数周期,计算点数
f=[ones(n1,1);zeros(n2,1);ones(n1,1);zeros(n2,1);ones(n1,1)];
% 构造周期矩形信号串
y=zeros(m+1,length(t));
y(m+1,:)=f';
figure(1);
h=plot(t,y(m+1,:)); % 绘制周期矩形信号串
set(h,'LineWidth',3*get(h,'LineWidth')); % 设置图形的线宽为原来的3倍
axis([-(T0+T1/2)-0.5,(T0+T1/2)+0.5,0,1.2]);
set(gca,'XTick',-T0-1:1:T0+1);
title('矩形信号串');
grid;
figure(2);
a=T1/T0;
pause; % 绘制离散幅度谱
freq=[-20:1:20];
mag=abs(a*sinc(a*freq));
h=stem(freq,mag);
set(h,'LineWidth',3*get(h,'LineWidth'));
x=a*ones(size(t));
title('离散幅度谱');
xlabel('f');
grid;
figure(3);
for k=1:m % 循环显示谐波叠加图形
pause;
x=x+2*a*sinc(a*k)*cos(2*pi*t*k/T0);
y(k,:)=x;% 计算叠加和
plot(t,y(m+1,:));
hold on;
h=plot(t,y(k,:));% 绘制各次叠加信号
set(h,'LineWidth',3*get(h,'LineWidth'));
hold off;
grid;
axis([-(T0+T1/2)-0.5,(T0+T1/2)+0.5,-0.5,1.5]);
title(strcat(num2str(k),'次谐波叠加'));
xlabel('t');
end
pause;
figure(4)
h=plot(t,y(1:m+1,:));
%axis([-T0/2,T0/2,-0.5,1.5]); % 显示一个方波
axis([-6,6,-0.5,1.5]); % 显示矩形脉冲串
title('各次谐波叠加');
xlabel('t');
grid;
=======================================================
参考书: 赵静,张瑾等. 基于MATLAB的通信系统仿真[M]. 北京:北京航空航天大学出版社,2007. 33-35
 爱华网
爱华网