初一下数学题 ab在数轴如图所示化简
一、填空:
1、单项式 的系数是 ,次数是 。
2、 是 次 项式,常数项是 。
3、 的各项是 最高次项是 ,常数项是 。
4、把多项式 按x的降幂排列为 按x的升幂排列为 。
5、若多项式 ,不含x3和x项则a= ,b= 。
6、(1)当a= 时,8-(2a+1)2有最大值 ,最大值是 。
(2)若(a-b)2-10有最小值,则最小值是 ,且此时a、b之间的关系是 。
二、选择题:
1、代数式x2,-abc, ,x+y,0, 中单项式的个数为( )
A、4 B、5 C、6 D、7
2、组成多项式8x2-4x-9的各项是( )
A、8x2,4x,9 B、8x2,-4x,-9 C、8,-4,-9 D、8x2-4x-9
3、下列说法正确的是( )
A、x3yz4没有系数,次数是7 B、 不是单项式,也不是整式
C、5- 是多项式 D、x3+1是三次二项式
4、如果一个多项式的次数是9,那么这个多项式任何一个项的次数( )
A、都小于9 B、都等于9 C、都不小于9 D、都不大于9
5、二次三项式ax2+bx+c为一次单项式的条件( )
A、a≠0,b=0,c=0 B、a=0,b≠0,c=0
C、a=0,b=0,c≠0 D、a=0,b=0,c=0
6、多项式-6y3+4xy2-x2+3x3y是按( )排列
A、x的升幂 B、x的降幂 C、y的升幂 D、y的降幂
7、多项式2x3-x2y2+y3+25的次数是( )
A、二次 B、三次 C、四次 D、五次
8、下列说法正确的是( )
A、 是多项 B、 是四次四项式
C、 的项数和次数等于6 D、 是整式
9、若m,n为自然数,则多项式xm-yn-4m+n的次数应是( )
A、m B、m+n C、n D、m,n中较大的数
10、若 是四次三项式,则n3=
A、-8 B、8 C、±8 D、不能确定
三、已知多项式 是六次四项式,单项式 与该多项式的次数相同,求m、n的值。
四、当a为何值时,化简式子 可得关于x的二次三项式。
五、已知 是关于x、y的5次单项式,试求下列代数式的值:
(1) (2)
由(1)、(2)两小题的结果,你有什么想法?
2.整式的乘除
一、选择题:
(1) ( )
(A) (B) (C) (D)
(2)下列运算正确的是( )
(A) (B) (C) (D)
(3) ( )
(A) (B)1 (C)0 (D)2003
(4)设 ,则 ( )
(A) (B) (C) (D)
(5)用科学记数方法表示 ,得( )
(A) (B) (C) (D)
(6)已知
(A) (B) (C) (D)
(7)
(A) (B) (C) (D)52
(8)一个正方形的边长增加了 ,面积相应增加了 ,则这个正方形的边长为( )
(A)6cm (B)5cm (C)8cm (D)7cm
(9)以下各题中运算正确的是( )
(A) (B)
(C)
(D)
(10) ,横线上应填的式子是( )
(11)
(A) (B) (C) (D)
(12) ( )
(A) (B) (C) (D)
(13)计算结果是 的是( )
(A)(x-1)(x+18) (B)(x+2)(x+9) (C)(x-3)(x+6) (D)(x-2)(x+9)
(14) ( )
(A)50 (B)-5 (C)15 (D)
(15)一个多项式的平方是 ,则 ( )。
(A) (B) (C) (D)
二、 填空题:
(1) _______。
(2) _______。
(3)设 是一个完全平方式,则 =_______。
(4)已知 ,那么 _______。
*(5)计算: _______。
(6)方程 的解是_______。
(7) _______。
(8)已知 。
(9) , , 。
三、计算题:
*
6、解方程
四、先化简,再求值: 其中 。(7分)
五、已知 的值。(7分)(*)
六、 计算阴影的面积(6分)
正方形的边长是 。 小正方形的边长是 空白长方形的宽是 求阴影的面积。
3.第一章测试题
一、选择题
1.多项式 的项数、次数分别是( ).
A.3、4B.4、4C.3、3D.4、3
2.若0.5a2by与 axb的和仍是单项式,则正确的是 ( )
A.x=2,y=0B.x=-2,y=0 C.x=-2,y=1D.x=2,y=1
3.减去-2x后,等于4x2-3x-5的代数式是 ( )
A.4x2-5x-5B.-4x2+5x+5 C.4x2-x-5D.4x2-5
4.下列计算中正确的是 ( )
A.an•a2=a2nB.(a3)2=a5C.x4•x3•x=x7D.a2n-3÷a3-n=a3n-6
5.x2m+1可写作( )
A.(x2)m+1B.(xm)2+1C.x•x2mD.(xm)m+1
6.如果x2-kx-ab=(x-a)(x+b),则k应为( )
A.a+bB.a-bC.b-aD.-a-b
7. 等于( ).
A. B. C. D.
8.若a≠b,下列各式中成立的是( )
A.(a+b)2=(-a+b)2B.(a+b)(a-b)=(b+a)(b-a)
C.(a-b)2n=(b-a)2nD.(a-b)3=(b-a)3
9.若a+b=-1,则a2+b2+2ab的值为 ( )
A.1B.-1C.3D.-3
10.两个连续奇数的平方差是 ( )
A.6的倍数B.8的倍数 C.12的倍数D.16的倍数
二、填空题
11.一个十位数字是a,个位数学是b的两位数表示为10a+b,交换这个两位数的十位数字和个位数字,又得一个新的两位数,前后两个数的差是 .
12. x+y=-3,则5-2x-2y=_____.
13. 已知(9n)2=38,则n=_____.
14.若(x+5)(x-7)=x2+mx+n,则m=__________,n=________.
15.(2a-b)( )=b2-4a2.
16.(x-2y+1)(x-2y-1)2=( )2-( )2=_______________.
17.若m2+m-1=0,则m3+2m2+2008= .
三、计算题
18.(3)(2a-3b)2(2a+3b)2;
19.(2x+5y)(2x-5y)(-4x2-25y2);
20.(x-3)(2x+1)-3(2x-1)2.
21.4a2x2•(- a4x3y3)÷(- a5xy2);
22.(20an-2bn-14an-1bn+1+8a2nb)÷(-2an-3b);
四、解答题
23.已知 =5, =10,求 .
24.已知多项式 除以一个多项式A,得商式为 ,余式为 。求这个多项式.
25.当 时,代数式 的值为6,试求当 时, 的值.
26.已知(a+b)2=10,(a-b)2=2,求a2+b2,ab的值.
27.已知a+b=5,ab=7,求 ,a2-ab+b2的值.
28.已知a2+b2+c2=ab+bc+ac,求证a=b=c.
29.已知a2+6a+b2-10b+34=0,求代数式(2a+b)(3a-2b)+4ab的值.
4.平行线与相交线
一.填空题(每小题2分,共48分)
1.如图(1)是一块三角板,且 ,则 。
2.若 则 的关系是 。
3.若 则 的关系是 。
4.若 则 的关系是 ,
理由是 。
5.若 则 的关系是 ,
理由是 。
6.如图(2)中,在RtΔABC中,∠ACB=90°,CD⊥AB,则图中
与∠A相等的角有 ,与∠A互余的角有
7.如图(3)是一把剪刀,其中 ,则 ,
其理由是 。
8.如图(4), 则AB与CD的关系是
,理由是 。
9.如图(5),∠1的同位角是 , ∠1的内错角是 ,若∠1=∠BCD,
则 ∥ ,根据是 。
若∠1=∠EFG,则 ∥ ,根据是 。
10.已知:如图6,∠B+∠A=180°,则 ∥ ,理由是 。
∵∠B+∠C=180(已知),∴ ∥ ( )。
11.如图7,直线a与b的关系是 。
二.选择题(每小题3分,共12分)
1.如图OC⊥AB于O点,∠1=∠2,则图中互余的角共有( )
A、2对 B、3对 C、4对 D、5对
2.下列说法正确的是( )
A、相等的角是对顶角 B、对顶角相等
C、两条直线相交所成的角是对顶角 D、有公共顶点且又相等的角是对顶角。
2.下列说法正确的是( )
A、邻补角是互补的角 B、锐角小于它的余角
C、锐角大于它的余角 D、34°的角的余角是66°的角
3.如图示,直线a、b都与直线c相交,下列条件中,能说明a∥b的是( )
①∠1=∠2;②∠2=∠8;③∠2=∠8;④∠1+∠4=180°
A、①② B、①②③ C、①②④ D、①②③④
4.下列说法不正确的是( )
A、同旁内角相等,两直线平行 B、内错角相等,两直线平行
C、同位角相等,两直线平行 D、若两个角的和是180°,则这两个角互补
三.解答下列各题:
1.(16分)如图,直线BC与DE相交,请分别指出图的对顶角、内错角、同位角和同旁内角。
对顶角有:
同位角有:
内错角有:
同旁内角有:
2.(8分)已知∠1与∠2互余,∠2与∠3互补,且∠3=36°求∠1的度数。
3.(10分)一个角的余角是它的补角的 ,求这个角的度数。
4.(6分)如图示,木工师傅用角尺画出工件边缘的两条垂线,这两条垂线平行吗?
为什么?
5.平行线的判定与性质
一、选择题
1.下列命题中,不正确的是____ [ ]
A.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行
B.两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
C.两条直线被第三条直线所截,那么这两条直线平行
D.如果两条直线都和第三条直线平行,那么这两条直线也互相平行
2.如图,可以得到DE∥BC的条件是______ [ ]
A.∠ACB=∠BAC B.∠ABC+∠BAE=180° C.∠ACB+∠BAD=180° D.∠ACB=∠BAD
3.如图,直线a、b被直线c所截,现给出下列四个条件:
(1)∠1=∠2,(2)∠3=∠6,(3)∠4+∠7=180°,(4)∠5+∠8=180°,
其中能判定a∥b的条件是_________[ ]
A.(1)(3) B.(2)(4) C.(1)(3)(4) D.(1)(2)(3)(4)
4.一辆汽车在笔直的公路上行驶,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是________[ ]
A.第一次向右拐40°,第二次向左拐40° B.第一次向右拐50°,第二次向左拐130°
C.第一次向右拐50°,第二次向右拐130° D.第一次向左拐50°,第二次向左拐130°
5.如图,如果∠1=∠2,那么下面结论正确的是_________.[ ]
A.AD∥BC B.AB∥CD C.∠3=∠4 D.∠A=∠C
6.如图1,a∥b,a、b被c所截,得到∠1=∠2的依据是( )
A.两直线平行,同位角相等 B.两直线平行,内错角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
(1) (2) (3)
7.同一平面内有四条直线a、b、c、d,若a∥b,a⊥c,b⊥d,则直线c、d的位置关系为( )
A.互相垂直 B.互相平行 C.相交 D.无法确定
8.如图2,AB∥CD,那么( )
A.∠1=∠4 B.∠1=∠3 C.∠2=∠3 D.∠1=∠5
9.如图3,在平行四边形ABCD中,下列各式不一定正确的是( )
A.∠1+∠2=180° B.∠2+∠3=180°
C.∠3+∠4=180° D.∠2+∠4=180°
10.如图4,AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC的度数为( )
A.30° B.60° C.90° D.120°
(4)
二、填空题
11.如图,由下列条件可判定哪两条直线平行,并说明根据.
(1)∠1=∠2,________________________.(2)∠A=∠3,________________________.(3)∠ABC+∠C=180°,________________________.
12.如果两条直线被第三条直线所截,一组同旁内角的度数之比为3∶2,差为36°,那么这两条直线的位置关系是________.
13.同垂直于一条直线的两条直线________.
14.如图,直线EF分别交AB、CD于G、H.∠1=60°,∠2=120°,那么直线AB与CD的关系是________,理由是:____________________________________________.
三、解答题
15.已知:如图,∠1=∠2,∠3=100°,∠B=80°.求证:EF∥CD.
16.已知:如图,FA⊥AC,EB⊥AC,垂足分别为A、B,且∠BED+∠D=180°.
求证:AF∥CD.
17.如图,已知∠AMB=∠EBF,∠BCN=∠BDE,求证:∠CAF=∠AFD.
18.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角A是120°,第二次拐的角B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,问∠C是多少度?说明你的理由.
19.(1)如图,若AB∥DE,∠B=135°,∠D=145°,你能求出∠C的度数吗?
(2)在AB∥DE的条件下,你能得出∠B、∠C、∠D之间的数量关系吗?并说明理由.
20.如图,在折线ABCDEFG中,已知∠1=∠2=∠3=∠4=∠5,延长AB、GF交于点M.试探索∠AMG与∠3的关系,并说明理由.
6.第二章测试题
一 选择题
1下面四个图形中,∠1与∠2是对顶角的图形的个数是( )
A.0 B. 1 C.2 D. 3
2 如图,若m∥n,∠1 = 105°,则∠2 =( )
A.55° B.60° C.65° D.75°
3 下列说法正确的是( )
A.经过一点有一条直线与已知直线平行
B.经过一点有无数条直线与已知直线平行
C.经过一点有且只有一条直线与已知直线平行
D.经过直线外一点有且只有一条直线与已知直线平行
4 已知:如图所示,直线AB、CD相交于O,OD平分∠BOE,∠AOC=42°,则∠AOE的度数为( )
A. 126° B. 96° C. 102° D. 138°
5 如图,∠1=∠2,则下列结论一定成立的是( )
A.AB∥CD B.AD∥BC C.∠B=∠D D.∠3=∠4
6 下列说法正确的个数是( )
①如果两个角相等,那么这两个角是对顶角;
②对顶角的平分线在同一条直线上;
③如果两个角有公共顶点,且角平分线互为反向延长线,那么这两个角是对顶¬角;
④如果两个角是对顶角,那么这两个角相等.
A.0个 B.1个 C.2个 D.3个
7 如图所示,下列推理正确的是( )
A.∵∠1=∠4,∴BC∥AD
B.∵∠2=∠3,∴AB∥CD
C.∵AB∥CD,∴∠BCD+∠ADC=180°
D.∵∠1+∠2+∠C=180°,∴AB∥CD
8 下列命题中,错误的是( )
A.邻补角是互补的角 B.互补的角若相等,则此两角是直角
C.两个锐角的和是锐角 D.一个角的两个邻补角是对顶角
二 填空题
9 已知, 与 是对顶角, ,则 (3分)
10 若a⊥c,b⊥c,则a b (3分)
11 推理填空:
如图 ① 若∠1=∠2
则 ∥ ( )
若∠DAB+∠ABC=1800
则 ∥ ( )
② 当 ∥ 时
∠ C+∠ABC=1800 ( )
当 ∥ 时
∠3=∠C ( ) (8分)
12 如图,AB∥CD,∠2 = 2∠1,则∠2 = (3分)
13命题“两直线平行,内错角相等”的题设是 结论是 (4分)
14下列哪个图形是由左图平移得到的 (3分)
三 解答题
15 △ABC在网格中如图所示,请根据下列提示作图。(6分)
(1)向上平移2个单位长度.
(2)再向右移3个单位长度.
16 如图,有两堵墙,要测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外。如何测量(运用本章知识)?(6分)
17如图,∠D =∠A,∠B =∠FCB,求证:ED∥CF。(6分)
18 如图,AD是∠EAC的平分线,AD∥BC,∠B = 30°,请求出∠EAD、∠DAC、∠C的度数.
(8分)
19 如图,⑴ 与 , 与 分别是哪两条直线被哪一条直线所截而成的?它们各是什么角?⑵请写出 的同位角?(9分)
20如图是进行跳远比赛时用的沙坑,运动员小陈从起跳线 上的A点跳到沙坑里的B点。请在图中画出测量小陈跳远成绩的线段,如果图中比例尺是1:250 ,试算出小陈跳远的成绩。 (8分)
21 如图,直线DE经过点A,DE∥BC,∠B=44°,∠C=57° (9分)
(1)∠DAB等于多少度?为什么? D A E
(2)∠EAC等于多少度?为什么?
(3)∠BAC等于多少度?
B C
7. 第三章 测试题
一、填空题
1、已知太阳的半径约为696000千米,用科学计数法表示为 千米。
2、常用的统计图有 、 和 三种。
3、在扇形统计图中,各个扇形面积的比为4∶3∶2∶1,则它们各自的圆心角的度数分别是 、 、 、 。
4、若3070000=3.07×10 x ,则x= 。
5、七年级(1)班某次数学测验成绩情况如下:优秀20人,良好30人,及格10人,如果将其制成扇形统计图,则三个扇形的圆心角分别为 、 、 。
6、右图是某钢铁厂生产甲、乙、丙三种型号的钢铁所占整个工厂生产
总值的百分比,则甲、乙、丙三种型号的产量比是 。
7、下图是某中学七年级(2)一次数学单元测试的成绩统计图,根据统计图,回答下列问题:①全班一共有 人;②成绩在 分的人数最多。
8、已知世界人口变化情况折线统计图如下图所示,则世界人口从40亿增加到60亿共花了 年;到2025年时,世界人口是 亿人。
9、右图是某农场种植三种蔬菜面积的扇形统计图,如果西红柿的种植面积为4.2公顷,则三种蔬菜种植的总面积是 公顷 ;黄瓜的种植面积是 公顷。
10、已知七年级(1)班语文测验成绩情况如下:优秀20人,良好30人,及格10人。则将其制成扇形统计图后,三个圆心角的度数分别是 、
、 。
二、选择题
11、已知小刚每走一步的长约为0.4米,则他走1万步的路程约为( )米
A、40米 B、400米 C、4000米 D、40000米
12、在一扇形统计图中,有一扇形的圆心角为60°,则此扇形占整个圆的( )
A、 B、 C、 D、
13、在扇形统计图中,若将圆均匀等分为12等分,则每一份对应的扇形圆心角为( )
A、45° B、60° C、30° D、90°
14、已知甲学校的男生占全校人数的50%,乙学校的女生占该校总人数的50%,则下列结论中,正确的是( )
A、甲校的男生与乙校的女生人数一样多
B、甲校的女生与乙校的男生人数一样多
C、甲校的男生比乙校的女生多
D、不能确定
三、解答题
15、建国以来,我国已经进行了五次人口普查,下表是历次普查得到的全国人口数量表:
普查年份1953年1964年1982年1990年2000年
人口数(亿)5.946.9510.0811.3412.95
请你根据以上数据制作一个统计图,并回答下列问题:
(1)1953年~2000年,我国人口增加了多少亿?
(2)五次人口普查中,从普查的结果看,哪一次增长速度快些?
16、下表是某省2002年人口普查中,每10万人受教育程度的统计表:
受教育程度大学高中初中小学
人数3331110363663432736
请将这次人口普查的受教育程度的统计资料,绘成一个扇形统计图。
17、请你用计算器算出一年共有多少秒(用科学计数法表示)?
18、已知某市有4类学校,各类学校所占比例如下表所示:
学校幼儿园小学中学特殊教育
百分比36%32%22%10%
(1)请你计算出各类学校对应的扇形圆心角的度数;
(2)哪两类学校较多,占比例是多少?
(3)若该市有5所特殊学校,则该市共有多少所中学?
19、请你测量一册七年级数学课本的厚度,然后判断100万册这样的课本叠在一起,有多高?如果你班的教室面积为80㎡,教室高为4m,估计你的教室能否装下100万册这样数学课本?
8. 第四章测试题
一、选择题
1. 下列事件发生的概率为0的是( )
A.小明的爸爸买体彩中了大奖 B.小强的体重只有25公斤
C.将来的某年会有370天 D .未来三天必有强降雨
2.小明用一枚均匀的硬币试验,前7次掷得的结果都是反面向上,如果将第8次掷得反面向上的概率记为P,则( )
A.P=0.5 B.P<0.5 C.P>0.5 D.无法确定
3. 一幅扑克去掉大小王后,从中任抽一张是红桃的概率是( )
A. B. C. D.
4.一个袋中有a只红球,b只黄球,它们除颜色不同外,其它均相同,若从中摸出一个球是红球的概率为 ( )
A. B. C. D .
5. 小狗在如图所示的方砖上走来走去,最终停在黑色方砖上的概率为( )
A. B. C. D .
6. 一次抽奖活动中,印发奖券1000张,其中一等奖20张,二等奖80张,三等奖200张,那么第一位抽奖者(仅买一张奖券)中奖的机会是( )
A. B. C. D.
7.四张卡片分别标有0、1、2、3的数字,抽出一张的数字是偶数的概率为( )
A. B. C. D.2
8.下列说法正确的是( )
A.小强今年12岁,明年百分之二百地是13岁.
B.同时抛掷两枚硬币,同是正面或同是反面朝上的可能性比一正一反大.
C.任意掷出一枚骰子,点数6朝上的概率与点数1朝上的概率相同.
D.盒子里装有10个完全相同的纸团,其中只有一个纸团内写有“奖”,而另九个纸团内均为“谢谢惠顾”,10名参与者可从中任摸一个纸团,则先摸的比后摸的“中奖”概率要大.
9.图中有四个可以自由转动的转盘,每个转盘被分成若干等分,转动转盘,当转盘停止后,指针指向白色区域的概率相同的是( ).
A.转盘2与转盘3 B. 转盘2与转盘4 C. 转盘3与转盘4 D. 转盘1与转盘4
10. 李明用6个球设计了一个摸球游戏,共有四种方案,肯定不能成功的是( )
A.摸到黄球 、红球的概率是 B.摸到黄球的概率是 ,摸到红球、白球的概率都是
C.摸到黄球、红球、白球的概率分别为 、 、 D.摸到黄球、红球、白球的概率都是
二.填空题:
11.小明在一个小正方体的六个面上分别标了1、2、3、4、5、6六个数字,随意地掷出小正方体,则P(掷出地数字小于7)=________.P(掷出地数字等于7)=________.
12、王刚设计了一个转盘游戏:随意转动转盘,使指针最后落在红色区域的概率为1/3,如果他将转盘等分成12份,则红色区域应占的份数是 .
13.同地掷出两枚硬币,则同为正面朝上的概率为 .
14.有大小两个同心圆,它们的半径分别是1和3,飞镖钉在小圆中的概率是
15.一个袋子中装有5个白球,3个红球,甲摸到白球胜,乙摸到红球胜,为使甲、乙两人获胜的可能性一样大,那么必须往袋中再放入 个 球.
16.如图,是由边长分别为2a和a的两个正方形组成,
闭上眼睛,由针随意扎这个图形,小孔出现在阴影部
分的概率是 .
三、解答题
21.(本题4分) 请将下列事件发生的概率标在下图中.(标序号)
⑴.十五的月亮就像一个弯弯细勾;⑵.正常情况下,气温低于零摄氏度,水会结冰;⑶.任意掷一枚六面分别写有1、2、3、4、5、6的均匀骰子,“3”朝上;⑷.从装有5个红球,22个白球,3个黄球的口袋中任取一个球,恰好是红球(这些球除颜色外完全相同).
22.(本题8分)中国民间流传“石头、剪刀、布”游戏,它们的规则是这样的:甲、乙两人同时出一种手势,手势是拳头则代表“石头”,伸出中指和食指代表“剪子”,伸出五指代表“布”.如果甲的手势是“剪刀”,乙的手势是“布”,因剪子可以剪布,则甲胜. 如果甲的手势是“剪刀”,乙的手势是“石头”,因石头可以砸剪子,则乙胜. 如果甲的手势是“布”,乙的手势是“石头”,因布可以包石头,则甲胜.请你填写下表,再根据表中结果说明这个游戏对双方是否公平?说明理由
甲的手势石头石头石头剪子剪子剪子布布布
乙的手势石头剪子布石头剪子布石头剪子布
结 果平胜负
23. 某高级酒店为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费100以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准九折、八折、七折、五折区域顾客就可以获得此项待遇(转盘等分成6份)
⑴甲顾客消费80元,是否可获得转动转盘的机会?
⑵乙顾客消费150元,获得打折待遇的概率是多少?
他获得九折,八折,七折,五折待遇的概率分别是多少?
24. (本题9分)小明外出游玩时,带了2件上衣和3条长裤,上衣颜色有白色、蓝色,长裤有白色、黑色、蓝色:
①小明随意拿出一条裤子和一件上衣配成一套,列出所有可能出现结果的“树状图”
②他任意拿出一件上衣和一条长裤穿上的颜色正好相同的概率是多少?
③小明正好拿出黑色长裤的概率是多少?
25.(本题7分)甲、乙两人打赌,甲说,往图中的区域掷石子,它一定会落在阴影部分上,乙说决不会落在阴影部分上,你认为谁获胜的概率较大?通过计算说明.
26.(12分)下表是高三某班被录取到高一级学校的学生情况统计表
重点普通其他合计
男生1871
女生16102
合计
完成表格
求下列各事件的概率
①P(录取到重点学校的学生)
②②P(录取到普通学校的学生)
③ P(录取到非重点学校的学生)
9. 期中测试题
一、精心选一选(每小题3分,共30分)
1、下列各组中,不是同类项的是( )
A、4xy3与5y3x B、6与 C、-9m2n与9m2n D、2abc与2bcd
2、下列说法正确的是( )
A、相等的角是对顶角 B、同位角相等
C、两直线平行,同旁内角相等 D、同角的补角相等
3、如图,由∠1=∠2,则可得出( )
A、AD∥BC B、AB∥CD
C、AD∥BC且AB∥CD D、∠3=∠4
4、由四舍五入法得到的近似数0.030570有效数字有( )
A、3个 B、4个 C、5个 D、6个
5、一个游戏的中奖率是1%,小花买100张奖券,下列说法正确的是( )
A、一定会中奖 B、一定不中奖如图所示,
C、中奖的可能性大 D中奖的可能性小
6、下列算式能用平方差公式计算的是( )
A、(3a+b)(3b-a) B( x+1)( - x-1) C、(2x-y)(-2x+y) D、(-m+n)(-m-n)
7、若x 2+ax+9=(x +3)2,则a的值为 ( )
A、3 B、±3 C、6 D、±6
8、一只小鸟在地砖上自由觅食,它最终停在白色方砖上的概率为 ( )
A、 B、 C、 D、
9、已知:am=3,an=5,则a3m-2n的值是( )
A、-1 B、2 C 、 D、-675
10、如图,把矩形ABCD沿EF对折,若∠1 = 500,
则∠AEF等于 .
A 500 B 800 C 650 D 1150
二、用心填一填(每空2分,共25分)
11、 是 项式,最高次项的次数和系数分别是 .
1 2、∠1与∠2互余,∠2与∠3互补,∠1=63°,那么∠3=
13、小刚的身高约为154cm,这个数精确到 位,将这个数保留两个有效数字是 m.
14、有资料表明,被称为“地球之肺”的森林正以每年15000000公顷的速度从地球上消失,每年森林的消失量用科学记数法表示为______________公顷。
15、从一个不透明的箱子内,摸出红球的概率为 。已知箱子里面红球的个数为6则箱子里共有球 个
16、图(1),当剪子口∠AOB增大15°时,∠COD增大 °
17、吸管吸易拉罐内的饮料时,如图(2),∠1=110°,则∠2= (易拉罐的上下底面互相平行)
图(1) 图(2) 图(3)
18、平行的大楼顶部各有一个射灯,当光柱相交时,如图(3),∠1+∠2+∠3=___
19阅读并填空:(此题每空1分)已知:△ABC, ∠A、∠B、∠C之和为多少?为什么?
解:∠A+∠B+∠C=
理由:作∠ACD=∠A,并延长BC到E
∠1=∠A(已作)
∴AB∥CD ( )
∴∠B= ( )
而∠ACB+∠1+∠2=
∴∠ACB+ + = (等量代换)
三、解答题(共45分)
20、计算题(每题3分,共15分)
9(x+2)(x-2)-(3x-2)2
(2x-y+1)(2x+y-1)
(用乘法公式计算)
21. (4分)化简求值:[(2a+b)2-(b-a)(a+b)]÷2a 此时a=2,b=-
22(4分)已知∠AOB,点P在OA上,请以P为顶点,PA为一边作∠APC=∠O
(不写作法,但必须保留作图痕迹)
问:PC与OB一定平行吗?
答:
23(4分)如图,已知:∠1=120°,∠C=60°,说明AB∥CD的理由。
24、(5分)已知AB∥CD, BE、CF平分∠ABC,∠BCD
探索BE与CF的位置关系,并说明理由。
25、(4分)下面是我国几个城市今年三月份的平均降水量。
地区昆明广州 海口上海
降水量(毫升)11332244
你能制作形象的统计图表示这几个地区三月份的平均降水量吗?
26. (4分)一个小妹妹将10盒蔬菜的标签全部撕掉了。现在每一个盒子看上去都一样,但是她知道有三盒玉米、两盒菠菜、四盒豆角、一盒土豆,她随机地拿出一盒打开它。求:
(1)盒子里是玉米的概率是多少?(2)盒子里面是豆角的概率是多少?
(3)盒子里不是菠菜的概率是多少?(4)盒子里是豆角或土豆的概率是多少?
27. (5分)如图,已知AB//CD,猜想图1、图2、图3中∠B,∠BED,∠D之间有什么关系?请用等式表示出它们的关系,并对其中的一个等式说明理由。
○1 ○2 ○3
10.三角形(1)
一、请准确填空(每小题3分,共24分)
1.如图1所示, ∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论是__________________.(注:将你认为正确的结论填上)
2.如图2所示,在△ABC和△DCB中,AB=DC,要使△ABO≌DCO,请你补充条件________________(只填写一个你认为合适的条件).
图1 图2 图3
3.如图3所示,在△ABC中,AD⊥BC,请你添加一个条件,写出一个正确结论(不在图中添加辅助线).条件是__________,结论为__________.
4.在△ABC和△ADC中,有下列三个论断:①AB=AD;②∠BAC=∠DAC;③BC=DC.将两个论断作为条件,另一个论断作为结论构成一个正确的因果关系,则条件是__________,结论为__________.
5.完成下列分析过程.
如图4所示,已知AB∥DC,AD∥BC,求证:AB=CD.
分析:要证AB=CD,只要证△________≌△________;需先证∠________=∠________,∠________=∠________.
由已知“________∥________”,可推出∠________=∠________,________∥________,可推出∠________=∠________,且公共边________=________,因此,可以根据“________”判定△________≌△________.
6.如图5所示,已知AB=AC,∠B=∠C,BE=CD,则图中共有全等三角形________对,它们分别是________.
7.如图6所示,点F、C在线段BE 上,且∠1=∠2,BC=EF,若要使△ABC≌△DEF,则还需补充一个条件________,依据是________________.
图4 图5 图6 图7
8.如图7所示,已知线段a,用尺规作出△ABC,使AB=a,BC=AC=2a.
作法:(1)作一条线段AB=________;
(2)分别以_______、_______为圆心,以________为半径画弧,两弧交于C点;
(3)连接_______、_______,则△ABC就是所求作的三角形.
二、相信你的选择(每小题3分,共24分)
9.如图8所示,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是
图8
A.甲和乙B.乙和丙
C.只有乙D.只有丙
10.以长为13 cm、10 cm、5 cm、7 cm的四条线段中的三条线段为边可以画出三角形的个数为
A.1B.2C.3D.4
11.图9是人字型金属屋架的示意图,该屋架由BC、AC、BA、AD四段金属材料焊接而成,其中A、B、C、D四点均为焊接点,且AB=AC,D为BC的中点,假设焊接所需的四段金属材料已截好,并已标出BC段的中点D,那么,如果焊接工身边只有可检验直角的角尺,而又为了准确快速地焊接,他应该首先选取的两段金属材料及焊接点是
A.AD和BC,点DB.AB和AC,点A
C.AC和BC,点CD.AB和AD,点A
12.图10是一个由四根木条钉成的框架,拉动其中两根木条后,它的形状将会改变,若固定其形状,下列有四种加固木条的方法,不能固定形状的是钉在________两点上的木条.
A.A、FB.B、EC.C、AD.E、F
13.如图11所示,已知△ABC不是等边三角形,P是△ABC所在平面上一点,P不与点A重合且又不在直线BC上,要想使△PBC与△ABC全等,则这样的P点有
A.1个B.2个C.3个D.4个
14.如图12所示,已知△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,且AB=6 cm,则△DEB的周长为
A.9 cmB.5 cmC.6 cmD.不能确定
图9 图10 图11 图12
15.如图13所示,△ABC中,AB=BC=AC,∠B=∠C=60°,BD=CE,AD与BE相交于点P,则∠APE的度数是
A.45°B.55°C.75°D.60°
16.如图14所示,∠1=∠2,∠3=∠4,若证得BD=CD,则所用的判定两三角形全等的依据是
A.角角角B.角边角C.边角边D.角角边
图13 图14
三、考查你的基本功(共18分)
17.(10分)如图15所示,△ABC≌△DEF,AM、DN分别是△ABC和△DEF的角平分线,AM、DN相等吗?写出依据.因为AM、DN是两全等△ABC和△DEF的对应角∠BAC和∠EDF的平分线,所以AM、DN也叫两全等三角形的对应角的平分线.
图15
其他两对应角的角平分线也有此结果吗?(只写结论,不写过程)它们有什么规律,请用一句话表示出来.
18.(8分)如图16所示,BC=DE,BE=DC,求证:(1)BC∥DE;(2)∠A=∠ADE.
小明是这样想的,请你给小明的每个想法填上依据.
图16
连接BD,在△BCD和△DEB中,
BC=DE(________)
BE=DC(________)
BD=DB(________)
△BCD≌△DEB(________) ∠CBD=∠EDB(________)
BC∥DE(_____________) ∠A=∠ADE(_____________).
四、生活中的数学(共14分)
19.(7分)如图17所示,把两根钢条AA′、BB′的中点O连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳).只要量出A′B′的长度,就可以知道工件的内径AB是否符合标准,你能说出工人这样测量的道理吗?
图17
20.(7分)图18是某城市部分街道示意图,AB=CD,AD=BC,EF=FC,DF⊥EC.公交车甲从A站出发,按照A、D、E、F的顺序到达F站;公交车乙从A站出发,按着A、B、C、F的顺序到达F站.如果甲、乙分别从A站同时出发,在各自的路径运行中速度及所耽误的时间均相同,猜想哪一辆公交车先到达F站?为什么?
图18
五、探究拓展与应用(共20分)
21.(10分)将两块形状完全相同的等腰直角三角板摆放成如图19所示的样子,假设图形中所有点、线都在同一平面内,那么图中共有多少对全等三角形?把它们一一写出,找出一对说出理由.(提示:等腰直角三角板两直角边相等,两锐角都是45°)
图19
11.三角形(2)
一、请准确填空(每小题5分,共20分)
1.如图1所示,O是线段BC的中点,过O作直线l⊥BC,则直线l叫做线段BC的垂直平分线.
在l上任取一点A,连接AB、AC,则AB_______AC(填“>”“=”或“<”).另任取一点A′,连结A′B、A′C,则A′B_______A′C(填“>”“=”或“<”).总之在l上任一点到B、C的距离都__________(填“相等”或“不相等”),由此,我们可以得到一个规律:__________.
图1 图2
2.如图2所示,小明与小华玩跷跷板游戏,如果跷跷板中点O(支点)到地面的距离OD= 50 cm,当小华从水平位置下降到地面时,小明这时离地面的高度为________cm,其中的道理是__________(用一句话简述).
3.如图3所示,AD、A′D′分别是锐角△ABC和△A′B′C′中BC和B′C′上的高,且AB=A′B′,AD=A′D′.若使△ABC≌△A′B′C′,请你补充一个条件________(只填一个你认为正确的条件即可).
图3
4.如图4所示,AD⊥BC,垂足为O,OA=OD,AB=CD,则全等三角形有________和________,理由是________;则AB与CD的位置关系是________,理由是________.
图4
二、相信你的选择(每小题4分,共24分)
5.如图5所示,∠ADC=∠AEB=90°,那么补充下列一个条件,仍无法判定△ABE≌ △ACD的是
A.AD=AEB.∠B=∠C
C.BE=CDD.AB=AC
图5 图6 图7
6.如图6所示,△ABC中,高AD和BE相交于点H,且HA=HC,则
A.∠1<∠2B.∠1>∠2
C.∠1=∠2D.不能确定
7.如图7所示,已知∠C=90°,DE⊥AB,垂足为E,BC=BE.若AC=3 cm,则AD+DE等于
A.2 cmB.3 cmC.5 cmD.6 cm
8.如图8所示,已知点
更多阅读
在野外如何用土豆加盐发电生火 野外烧土豆
在野外如何用土豆加盐发电生火——简介在野外如何用土豆加盐发电生火。在野外如何用土豆加盐发电生火——工具/原料刀,土豆,盐,牙膏,电线,绒线或干草在野外如何用土豆加盐发电生火——方法/步骤在野外如何用土豆加盐发电生火 1、首先,用

已知,如图中,等边△ABC和点P,设点P到△ABC三边AB、AC、BC的距 三角形abc中ac等于bc
题文已知,如图中,等边△ABC和点P,设点P到△ABC三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高为h,若点P在一边BC上(如图①),此时h3=0,可得结论:h1+h2+h3=h。请直接应用上述信息解决下列问题:当点P在△ABC内(如图②)、点P在△ABC外(如图③)这两种
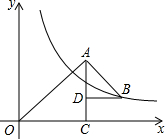
如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比 反比例函数讲解
(2014·济南)如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=kx在第一象限的图象经过点B.若OA2-AB2=12,则k的值为6.考点:反比例函数图象上点的坐标特征;平方差公式;等腰直角三角形.分析:设B点坐标为(a,b),根据等腰直角三角形

初中初一七年级下学期下册体育学科教学工作计划,方案下载大全 初一下学期英语辅导
七年级下学期体育教学工作计划本学期是七年级下学期,在认真钻研教学大纲和结和本校实际的基础上,制定出切实可行的教学计划。一:学生现状分析所任教的七年级学生年龄在13——14岁之间,处于青春发育的高峰期,身体发育较快,男女差别较大,男生
如图1,在Rt三角形abc中,角C等于90度,ac=8cm,bc=6cm,点 领带6cm还是8cm
为了解决用户可能碰到关于"如图1,在Rt三角形abc中,角C等于90度,ac=8cm,bc=6cm,点"相关的问题,突袭网经过收集整理为用户提供相关的解决办法,请注意,解决办法仅供参考,不代表本网同意其意见,如有任何问题请与本网联系。"如图1,在Rt三角形a
 爱华网
爱华网