发布时间:2018年04月10日 21:56:30分享人:戒不掉的小残忍来源:互联网14
题目 朋友,如果你自认为还有几分聪明, 请来准确无误地算一算太阳神的牛群, 它们聚集在西西里岛, 分成四群悠闲地品尝青草。第一群象乳汁一般白洁, 第二群闪耀着乌黑的光泽。 第三群棕黄, 第四群毛色花俏, 每群牛有公有母、有多有少。 先告诉你各群的公牛比例:白牛数等于棕牛数再加上黑牛数的三分之一又二分之一。 此外,黑牛数为花牛数的四分之一加五分之一,再加上全部棕公牛。朋友,你还必须牢记花牛数是白牛的六分之一又七分之一 再搭上全部的棕色公牛。 但是,各群的母牛都有不同的比例:白色的母牛数等于全部黑色公母牛的三分之一又四分之一。 而黑母牛又是全部花牛的四分之一加上五分之一, 请注意,母牛公牛都要算进去。同样的,花母牛的数字是全部棕牛的五分之一加六分之一。 最后,棕色母牛与全部白牛的六分之一加七分之一相一致。朋友,若你能确切地告诉我这些公牛母牛膘肥体壮、毛色各异, 一共有多少聚集在那里, 你就不愧为精通算计。 但你还称不上聪明无比,除非你能回答如下的问题: 把所有的黑白公牛齐集一起, 恰排成正方形,整整齐齐。 辽阔的西西里岛草地, 还有不少公牛在聚集。当棕色的公牛与花公牛走到一起, 排成一个三角形状。www.a7a1.com 棕色公牛、花公牛头头在场,其他的牛没有一头敢往里闯。 朋友,你若能够根据上述条件, 准确说出各种牛的数量, 那你就是胜利者, 你的声誉将如日月永放光芒。公元前3世纪下半叶古希腊科学家阿基米德在论着《群牛问题》中记载了本问题。原文用诗句写成,大意是:西西里岛草原上有一大群牛,公牛和母牛各有4种颜色。设W、X、Y、Z分别表示白、黑、黄、花色的公牛数,w、x、y、z分别表示这白、黑、黄、花色的母牛数。要求有W=(1/2+1/3)X+Y,X=(1/4+1/5)Z+Y,Z=(1/6+1/7)W+Y,w=(1/3+1/4)(X+x),x=(1/4+1/5)(Z+z),z=(1/5+1/6)(Y+y),y=(1/6+1/7)(W+w),(W+X)为一个正方形(数),(Y+Z)为一个三角数(即m(m+1)/2,m为正数)。求各种颜色牛的数目。最后两个条件中的正方形数有两种解释:一种是W+X=mn,(因为牛的身长与体宽不一样,排成正方形后两个边牛的数目不一样)称为「较简问题」,求解后牛的总数近6万亿,另一种为W+X=n2(长与宽的数目相等),称为「完全问题」。即使没有最后两个条件,群牛问题的最小正数解也达几百万到上千万。诗的大意是:西西里岛草原上有一大群牛,公牛和母牛各有4种颜色。设W、X、Y、Z分别表示白、黑、黄、花色的公牛数,w、x、y、z分别表示这白、黑、黄、花色的母牛数。
要求有
W=(1/2+1/3)X +Y,
X=(1/4+1/5)Z+Y,
Z=(1/6+1/7)W+Y,
w=(1/3+ 1/4)(X+x),
x=(1/4+1/5)(Z+z),
z=(1/5+1/6)(Y +y),
y=(1/6+1/7)(W+w),
(W+X)为一个正方形(数),
(Y+Z )为一个三角数(即形如m(m+1)/2的数,m为正整数)。
求各种颜色牛的数目。
倒数第二个条件中的正方形数有两种解释:
一种是W+X=mn,因为要挤成一个正方形,还需要考虑身长与体宽的比,故右端不是任意两个正整数之积mn而是kn^2(k是常数,称为「较简问题」
另一种为W+ X=n^2(完全平方数),即长与宽上牛的数目相等,称为「完全问题」。1880年阿姗托尔提供了一种解答,导致二元二次方程t2-du2=1,因d的值达400多万亿,所以完全问题的最小解中牛的总数已超过20多万位的数。可见阿基米德当时未必解出过这个问题,而它的叙述与实际也不符。历史上对这问题的研究丰富了初等数论的内容。阿基米德分牛问题的原题完全不是一个七岁小学生的奥数题目集里面可能出现的....小学奥数倒是有个简化题目。
太阳神有一牛群,由白、黑、花、棕四种颜色的公、母牛组成. 已知:
在公牛中,白牛数多于棕牛数,多出之数相当于黑牛数的1/2+1/3;黑牛数多于棕牛数,多出之数相当于花牛数的1/4+1/5;花牛数多于棕牛数,多出之数相当于白牛数的1/6+1/7.
在母牛中,白牛数是全体黑牛数的1/3+1/4;黑牛数是全体花牛数1/4+1/5;花牛数是全体棕牛数的1/5+1/6;棕牛数是全体白牛数的1/6+1/7.
问这牛群是怎样组成的?
如果是这个题目的话就不是那么难解了...不用二层楼的天才,直接谢三公子估计都能解出来了...所以说老猫这里的设定有些经不起推敲啊,牛逼的孩子小时候奥数学的再好,没有大学期间数学系系统的学习,所接触的题目终究不会有太高的难度(这个是相对于天才来说的),而宁缺明显只是因为小时候被家长逼着参加奥数班才有了比较扎实的数学基础,但是这些基础终归只是初等数学的范畴,高中奥赛的内容其实就是大学学习的各种理论.....
爱华网本文地址 » http://www.aihuau.com/a/25101013/153329.html
更多阅读

牛吃草问题又称为消长问题或牛顿牧场,是17世纪英国伟大的科学家牛顿提出来的。知鸟教育人事考试网的专家指出,典型牛吃草问题的条件是假设草的生长速度固定不变,不同头数的牛吃光同一片草地所需的天数各不相同,求若干头牛吃这片草地可以
很久没有看过这类型的小说了,犯罪推理。之前看过的只有丁墨的《他来了,请闭眼》和《如果蜗牛也有爱情》。而这一本其实看得我有些难过。为言溯,也为甄爱。其实就像作者写的,言溯是光明之子,而甄爱却一直生活在黑暗中。言溯就和任何言情小

[绝对原创,作者:KYLL][注1:北京大学作为中国首家首次招收彩票专业研究生的大学,不久前硕士招生考试举行,本文即作者的考试论文。][注2:为乐彩网友阅读方便及兴趣,本文删除了论文中烦闷的纯数学的理论分析,简化了数据规模,最大限度地降低了读

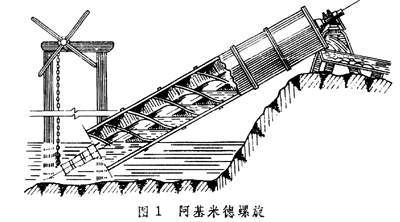
是阿基米德阿基米德(Archimedes, 公元前287~212年)是古希腊数学家、科学家和发明家.公元前287年生于古希腊在西西里岛的城邦叙拉古.他的父亲菲迪阿斯是一位天文学家,与叙拉古国王亥尼洛二世有亲戚关系.阿基米德是机械理论的创建者,当时社

姿嘉2级分类:文化/艺术被浏览62次2014.12.15检举孤独尤里乐帮达人采纳率:66%42级2014.12.15前言阿基米德(公元前287年—公元前212年),古希腊哲学家、数学家、物理学家,确定了许多物体表面积和体积的计算方法,发现了杠杆原理和浮力定律,出生

 爱华网
爱华网



