摘要:
我们发现了一种新型的振荡器,它可把连续的光信号转变成稳定性高、光谱纯度高的微波信号。该光电微波振荡器由泵浦激光器与光电反馈回路组成,其中光电反馈回路包括强度调制器、光纤延迟线,光电探测器,射频放大器,滤波器等器件。我们发现了一个准线性理论并得到了振荡器的阈值条件、振幅、频率、线宽和光谱功率密度的表达式,我们把理论数据与实验数据进行了比较。研究结果表明,光电微波振荡器能够产生超高稳定度,高光谱纯度的微波信号,产生微波信号的频率最高可达75GHz,偏离中心频率10KHz的相位噪声低于-140dBc/Hz。
引言:
振荡器是一种把连续的信号转换为周期性变化信号的装置。所有物理振荡器,谐波振荡器都是基于这种原理工作的,振荡器已经成为当今世界应用最广泛的设备之一。当今,各式各样的振荡器,例如机械振荡器(单摆)、电磁振荡器(LC振荡电路)和原子振荡器(微波激射器和激光器)提供了不同频率范围的信号。振荡器输出的微波信号的纯度和稳定度是对振荡器的好坏的一个衡量标准,它很大程度上取决于振荡器的能量储存能力,振荡器的能量存储能力与振荡器内部各个部件的损耗有关。
电子振荡器是其中应用最广泛的一种振荡器。真空电子管发明不久,L. De Forest 于1912年发明了世界上第一个电子振荡器。这些以三极管为基础的振荡器称为van der Pol 振荡器,其工作原理如图1(a):由真空管阴极发射流向阳极的电子受到栅极信号的调制,栅极调制信号是由阳极的信号经过带有存储能力的反馈电路进行产生的。
目前,这种基于晶体管的振荡器几乎遍布所有的电子设备,仪器和系统。由于这种基于晶体管的噪声与稳定度较差远远不能满足要求高光谱纯度和高的稳定度应用的场合。欧姆定律和振荡器内部元件的损耗大大限制了电子振荡器的发展。
近50年里科研工作者一直致力于减小电子振荡器的噪声特性,通过结合高品质因素的谐振腔可以大大改善信号的稳定性和频谱纯度。Q是用来描述谐振腔优劣的参数之一,定义为: ,式中 Td是能量衰减时间,用来描述谐振腔能量储存能力, f是谐振腔的谐振频率。用来提高电子振荡器的稳定性的高Q谐振器包括机械谐振腔(如石英振荡器)、电磁谐振腔(如电介质腔)、原子谐振腔、电延迟线。其中电子延迟线的延迟时间需正好等于能量衰减时间 ,从而获到最佳的品质因素Q。不管是那种振荡器,选择合适的高Q谐振腔非常重要,目前,通过选择适当的高Q谐振腔的晶体振荡器在频率稳定度方面获得了突破,但是石英振荡器只适用于产生低频信号,石英振荡器不能产生可调谐信号或高频信号。
这篇文章中我们介绍了一种新型的光电振荡器,它产生信号的光谱纯度和稳定性可以与最好的晶体振荡器相匹敌。图1(b)是这种振荡器的示意图,它可把连续的光能量转换为周期性变化的射频微波信号。 我们把光电振荡器简称为OEO,OEO的原理与van der Pol 振荡器相似,它利用光信号取代了van der Pol 振荡器的电信号,利用电光调制器来代替栅极的功能,利用光电探测器来取代阳极,利用长光纤延迟线取代van der Pol 振荡器中起能量储存功能的LC回路。
虽然OEO与电子振荡器的结构相似,但是OEO除具有晶体振荡器的高稳定性的特征外,还具备晶体振荡器无法与之相比的低相位噪声。这种优良特性是由于在OEO 使用了效率高,速率快,损耗低的E/O和光电元件,特别地,目前光电探测器的量子效率能达到90%,响应频率能够高达110GHz,而E/O调制器的响应频率也可以达到75GHz。最后,低损耗的光纤也是一个重要的原因,商用1550nm的光的损耗只有0.2dB/Km,使用这种损耗可以忽略不计的光纤存储回路就保证了存储单元的光能量存储时间足够长。
OEO的特性之一可以输出微波信号,也可以输出得到强度调制的光信号,这个性能在光学元件,光学设备和光学系统中的应用是非常重要的。
许多学者研究了含有E/O光电调制器的光电环型结构的光学器件的非线性机制。Neyer和Voges首次提出可以利用这种结构制作振荡器[20],但是大家感兴趣的是这种振荡器的非线性现象和混沌动力学特性。Aida和Vavis也一直进行该方面的研究,他们在光电反馈环所采用光纤波导作为延迟线。我们主要研究光电振荡器的稳定性和噪声特性,从理论和实验对这种准动力学特性进行了研究,利用反馈环消除了电光调制器产生的非线性特性,利用该方法产生了稳定性好,低相位噪声的信号,它与我们提出的准线性理论相吻合。
本文中首次介绍这种光电振荡器和工作的物理机制。我们提出了光电振荡器的动力学特性和振荡噪声特性的非线性理论,并把理论结果和实验结果进行了比较。
振荡器的描述:
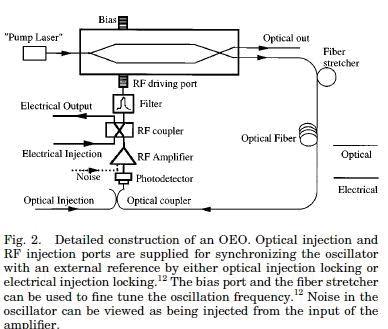
光电振荡器利用电光调制器和光纤延迟线中的传输特性将连续光转换成了稳定性好,频谱纯度高度的射频/微波信号。图2是光电振荡器详细的结构示意图。激光器输出连续光经过电光调制器后经过一段长光纤传输后进入光电探测器,光电探测器把光信号转换为电信号后再经过放大、滤波后反馈给调制器的电输入端。这种结构能够以特定频率实现自持振荡,其振荡的频率由光纤的长度,调制器的偏置和滤波器的带通特性来决定。该振荡器同时输出电信号和光信号,这在光子应用领域具有极大的优势。
我们利用再生反馈的方法分析了振荡器的光谱特性。这种方法已经成功的用于分析激光器和声表面波震荡器。维持自激振荡的条件是:再环路中的波信号需要连续的获得增益即在环路中,信号的单程增益需大于单程损耗才能获得稳定的震荡。维持自持震荡的第一个条件是:在所有起振的模式中,只有与基波信号的相位差必须满足2π的整数的模式才能起振。所以调制器和滤波器的频率响应特性只让满足条件的模式起振,从而抑制了其它模式的起振。第二个条件表明只要输入光的能量足够强,在环内不使用微波或射频放大器,振荡器本身就能够维持自激振荡。下述章节中详细阐述这些有希望用于定量分析振荡器的动态特性理论。
光电振荡器的准线性理论:
接下来我们研究了光电振荡器的动力学特性和噪声特性。在讨论中,我们假定电光调制器是马赫曾德尔型。对于使用其它调制器的振荡器,可用同样的方法进行分析。首先外环的光电特性由激光器,调制器,光纤延迟线和光电探测器决定。我们在调制器处形成一个环路,在回路中加入滤波器,然后采用准线性分析方法进行分析,采用这种方法得到了振荡器振荡的幅度和频率之间的公式。接下来我们分析了振荡器的噪声特性,主要是在回路中引入滤波器。最后得到适用于实验研究的光电振荡器谱密度表达式。
A 振荡阈值
电光调制器输出端的光功率于输入电压Vin(t)之间的关系式如下:
式中α 是调制器的插入损耗,Vπ是半波电压,VB是偏置电压,P0是注入光功率,η决定调制器的消光系数,即(1+η)(1-η)。
光功率P(t)通过光电探测器转换成电信号,经过射频放大后的电信号为:
这里的ρ是探测器的响应率,R是探测器的负载阻抗,GA是放大器的电压增益,Vph是光电压,定义为:
Iph=аP0ρ/2是光电流,注入电光调制器的电压由公式(2)来决定。因此OEO的小信号开环增益GS为:
当VB=0或者Vπ时,就得到最大的小信号增益。从公式4可以看出GS既可以是正也可以是负,主要取决于偏置电压。当调制器处于正向偏置电压的情况,如果GS>0,否则,调制器处于负的偏置电压。因此当,调制器的偏置积分为负;当VB=Vπ调制器的偏置积分为正。由此在不影响光电振荡器特性的条件下,电光调制器的偏压可以为正,也可以为负。但是我们发现,偏置的正负对OEO的运行机制具有很重要的影响。
为了让光电振荡器振荡,开环小信号增益必须大于单程回路的损耗。由公式(4)可以得到光电振荡器振荡阈值电压:
理想情况下η=1,VB=0或者VB=Vπ,公式(5)变为:
由公式(3)和公式(6)可以得到一个重要的结论,光路中的内的放大器不是振荡器的必然条件。只要满足Iph≥Vπ/π就不需要使用放大器(GA=1)。只要泵浦激光器能为OEO提供足够的能量,就可使得光电振荡器适用于厂距离光纤光路中,更重要的是,在光学回路中,如果不使用放大器就可以避免由放大器引入的噪声,这样光电振荡器的稳定性就能得到很大的改善。例如不使用放大器,假设光电探测器的响应度是0.8A/W,需要的光功率为25mW,当调制器的半波电压是3.14V,阻抗为50Ω,探测器的光电流为20mA时振荡器就能维持稳定的自激震荡。
B 电光调制线性响应函数
一般情况下,公式(2)是非线性的。如果注入调制器的电压Vin(t)是正弦波形式的,其角频率为ω,幅度为,初相位为β,即:
将公式(7)代入公式(2),并利用贝塞尔函数将公式(2)展开得到在探测器的输出电压为:
从公式(8)可以清晰地看出,输出中包含有很多ω的谐波分量。
当通过一个线宽足够窄的射频滤波器,滤去谐波项,将输出线性化。可以很容易地得到公式(8)的线性化公式:
这里电压增益G(V0)定义为:
由上公示可以发现电压增益是注入电压幅度的非线性函数,使得幅值随的变化而下降。对于足够小的注入信号 我们可以从公式(10a)得到小信号增益G(V0)=GS。如果我们利用泰勒公式对公式2左侧展开,增益系数变为:
一般情况下,G(V0)是注入信号的角频率ω的函数。因为Vph与射频放大和光电探测器的响应度是线性比例关系,这两个参数都与频率有关系。另外调制器的半波电压也是注入射频信号频率的函数。因此,射频滤波器的频率响应也集中到
G(V0)。在下面的讨论中我们引入一个无量纲的方程:
这里的Φ(ω)是一个与频率有关的相位项。这样通过监测正弦波的振幅与相位就可以监测到回路的噪声特性, F(ω)是规范化得传播函数。公式(9a)可以写成复杂的形式:
这里的 和 分别为注入和输出电压。虽然公式(9b)是线性的,调制器的非线性并没有消失,包含在非线性增益系数G(V0)中。
振荡频率与振幅:
在这一节我们讨论光电振荡器的频率和振幅的公式。与别的振荡器一样,光电振荡器最初也是初始短暂的噪声,输出信号经过反馈使振荡加强和持久。我们利用数学公式推导得到振荡器振幅的表达式。初始瞬间噪声可以看作是相位和幅度随机变化的正弦波。为了简化这个数学推导,利用公式(9b)的线性信号作为注入的噪声信号。因为公式(9b)是线性的,我们首先可以通过分析噪声信号单一频率的影响来分析OEO响应特性:
是在环内循环的次数, ,在公式(13)中G(V0)中的V0是环路中总的幅度。所有瞬时的总时间是所有流通的领域的总和。因此,注入电光调制器的射频信号可以用下式描述:
环路增益低于阈值,并且V0比较小,G(V0)实质上是公式(4)给出的小信号增益。相应地环路噪声频率ω的响应的射频功率为:
这里如果 时 ,如果 时 。对于瞬时 光电振荡器的频率相应产生的空间峰与FP相应类似,如图(3)所示。这些峰值在这些频率处被锁定,由下面公式决定:
这里的k是模式数,图(3)中每个峰对应的频率由该环和所有环共同响应的频率决定。当开放环路的获取增加,每个峰变得更大,并且它的形状变得更加锋利。这些峰是OEO的可能存在的振荡模式。当开环增益大于1,噪声会围绕着峰值,并且也被放大,振荡会变成噪声。
在环内有一个射频滤波器,只有一个模式的增益允许大于1,这样只有被选择的模式可以起振。由于电光调制或者射频放大器的非线性特性,振荡模式不能无限制地增大。随着幅度的增加,由于调制器或放大器的非线性效应,振荡会产生高次谐波,将会消耗一部分功率。这些高次谐波将会被射频滤波器滤掉。事实上,根据公式(10)振荡模式会的增益会一直增大到等于1时,振荡是很稳定的。下面将会看到,由于不断出现的噪声,闭环的增益会小于1,有一个微小的减小量,损失量为10-10,总量符合公式(14)。
在接下来的讨论中,只有一个模式k起振,我们用 表示该模式的频率,用Vosc表示该模式振荡的副度,振荡功率为 。在这种情况下,公式(15)中的总的幅度V0正好就是起振模式的幅度Vosc。如果选择的滤波器通过的峰为震荡模式ωosc且F(ωosc)=1,振荡幅度可以利用设置公式(15)中的增益系数∣G(Vosc)∣为1来解决。从公式(10a)我们可以得到: 在公式(17a)中,我们假设环内的射频放大是线性的,这样振荡幅度的限制主要是由调制器的非线性限制。振荡幅度可以由公式(17a)的曲线图来得到,如图4(a)所示。这种结果和Neyer和Voges用复杂的方法得到的结果一致。如果我们利用公式(10b),我们可以得到振荡幅度的近似值 ∣GS∣≥1的阈值条件可以由公式(17b)和(17c)可以得到。图4(a)表明正常振荡幅度增益就是公式(17a),(17b)和(17c)得到的∣GS∣。比较三条理想的曲线,三阶展开结果∣GS∣≤1.5,与现实非常接近。五阶展开结果是∣GS∣≤3。
可由公式(16)得到相对应的振荡频率为:
这里的T是环的总的群延迟时间,包括环的实际长度延迟时间 和环内元件色散引起的群延迟时间(如放大器)。可以由下式得到
实际上, ,信号的增益 是由小信号增益Cs来决定的。有公式(18)可以得到振荡频率是由调制器的偏置决定。当是负的偏置时 ,基频频率为 ,当是正的偏置的时 ,基频频率是1/T。
D 光谱
振荡器的基本噪声由热噪声、散弹噪声和激光器相对亮度噪声组成,为了进行分析,可以把这些噪声的来源是光电探测器。当光电探测器和放大器直接相连接时,噪声可以看作是有一个振荡器注入放大器放大器的信号。如图2所示。
我们计算振荡器信号的光谱来决定振荡器噪声的功率谱密度。设 是在频率为ω的情况下注入噪声的功率谱密度。我们得到: 这里的Δf 是频率线宽。将公式(20)代入公式(10),并假设 ,我们可以得到振荡模式K的功率谱密度是:
利用归一化条件:
我们得到:
在公式(22),我们假定振荡模式的光谱宽度远小于振荡模式间隔 1/T,所以得到的1/T是非常精确的。另外,我们已经假设在起源处 在总的频率线宽 从公式(23)可以得到振荡模式的闭环增益 比1一共小10-10。因此利用公式 已经能够相当精确地得到振幅Vosc。就像公式(17)。
最后,将公式(23)代入公式(21),我们得到光电振荡器的射频功率谱密度:
就像前面介绍的, 相当于从放大器的输入端注入振荡器的噪声密度。 是放大前总的振荡功率。所以δ是振荡器的信噪比。在 的情况下,利用泰勒展开公式对公式(24a)简化:
公式(24b)是非常接近理想, ,由于忽略泰勒展开的高次项造成的误差不足1%。由公式(24b)可以得到振荡模式的光谱密度是频率的洛伦兹函数。半高全宽是:
由公式(26a)很明显地看到半高全宽与环延迟时间的平方成反比。与诸如信噪比成正比。对于典型的情况下,δ为10-16/Hz,环的延迟为100ns(20m),得到的半高全宽是在亚MHz数量级。在半高全宽范围内包含的功率范围是
从公式(26a)还可以得到,对于固定的ρN和GA ,谱宽与振荡的能量成反比,与著名的Schawlow–Townes公式描述激光器的谱宽 很相似:
这里的ρS=hv是激光器的自发辐射噪声密度,Plaser是激光器振荡功率。Tlaser是激光器腔的延迟时间。但是,就像3-E部分介绍的,Posc和ρN都是光电流的函数。这表明只有在与热噪声密切相关的光电流很低的情况下,光电振荡器的谱宽与振荡功率成反比例关系。 振荡器的质量因素Q的公式为:
这里QD是环延迟线,定义为:
从公式(24b)可以轻松地得到:
可以发现振荡器的相位噪声波动远小于1,它的功率谱密度等于单边带相位噪声和单边带幅度噪声的总和。大多数情况下振幅波动远小于相位波动,功率谱密度正好等于单边带相位噪声。从公式(29b)可以清楚地看到光电振荡器的相位噪声与频率偏移量f ' 的二次方程反比关系。当频率偏移量f ' 固定的情况下,相位噪声随着环延迟时间的增加而减小。延迟时间T 越大,相位噪声越小。但是,无论延迟时间T 增加到多大,相位噪声也不可能降为0。当延迟时间增加到一定的情况下,公式(24b)和(29b)就不符合逻辑了。根据公式(24a),在f ' =1/2T情况下得到最小的相位噪声 。当频率偏移量超出环滤波器的带宽的时候 ,相位噪声可以简单地看作信噪比 ,可由公式(21)得到。
公式(24)和(29a)表明振荡器的相位噪声与振荡频率没有关系 。这个结果非常重要,这样利用光电振荡器就可以得到低相位噪声的高频信号。利用倍频的方法产生的信号的相位噪声与频率的二次方成正比。 E 信噪比
如前面所述,注入振荡器的总的噪声密度是热噪声 ,散弹噪声 和激光器相对亮度噪声 的和:
这里KB是波尔兹曼常数,T是环境温度,NF是噪声系数,e是电子电荷量,Iph是通过光电探测器负载电阻的光电流,NRIN是泵浦激光器的相对强度噪声。
从公式(25)和(30)可以发现,如果热噪声占主要地位, 与振荡器的振荡功率Posc成反比关系。一般情况下,Posc是光电流Iph和放大增益GA的函数,如公式(17)所述。公式(25)中的信噪比是:
从公式(31)可以看到 是振荡器小信号增益的非线性函数。如图5(a)所示,在 时,达到最小值: 这里假定η=1和cos(πVB/Vπ)。 时的振荡幅度可以由公式(17b)得到: 相对应的射频功率是:
这里的 是注入1dB电光调制器的压缩功率。由公式(33b)可以算出注入点光调制器的光功率应该至少大于调制器得到1dB的压缩功率所需的注入功率至少5dB。由公式(33b)还表明当振荡幅度大概是半波电压的一半或者振荡器的电压正弦曲线变化时振荡器的噪声最小。这是可以理解的,因为调制器具有它最小的敏感电压变化。
从公式(32)可以明显地看到,光电流越大,振荡器的信噪比越小,指导最后与相对亮度噪声水平相平。因此光电振荡器最终的信噪比要受到泵浦激光器的相对亮度噪声限制。 图5是不同的相对亮度噪声的情况下信噪比随着光电流的变化。
F 放大器的非线性效应
在上面的讨论中我们假定电光调制器输出信号的非线性曲线比振荡器用到的放大器的要严格。这样振荡幅度或者功率会受到电光调制器的非线性响应的限制。根据工程术语,放大器输出1dB压缩点功率远大于注入电光调制器的1dB压缩点功率。
对于放大器输出1dB压缩点功率小于注入电光调制器的1dB压缩点功率的情况,放大器的非线性现象将限制振荡器的振幅Vosc(或功率Posc),会导致振幅小于公式(17)的要求。如果知道放大器的非线性响应函数,也可以像公式(17)一样得到振幅和小信号增益之间的精确关系。假定振荡功率由放大器的非线性特性来决定,3D部分得到的关于振荡器的光谱的描述的公式任然符合逻辑。对于足够大的小信号增益,振荡功率会接近放大器输出的1dB压缩点功率。
在下面的试验中,选择放大器输出的1dB压缩点功率远大于注入调制器的1dB压缩点功率。这样振荡功率会受到调制器的限制。
实验:
A 幅度随着开环增益的变化
我们通过实验对上面的理论结果进行实验验证。在我们所有的实验中我们用一个非常稳定的二极管Nd:YAG环激光器和一个减小相对亮度噪声的环作为OEO的泵浦。测量振幅的开环增益的实验装置如图6(a)所示。用一个射频开关来控制环的开和闭。当处于开环状态的时候,一个与振荡器输出频率相同的射频信号注入调制器。利用示波器测量注入信号和从环输出信号的幅度,开环增益是输出信号的幅度与注入信号的幅度的比值。我们通过改变电光调制的电压或者环内光功率的衰减或者在光电探测器后增加一个射频衰减器来改变环的增益,如公式(4)所述。当是闭环的情况下这幅可以用一个示波器来测量。我们测量振荡频率为100MHz时,在不同闭环增益情况下光电振荡器的振幅。测量得到的数据如图4(b)所示。比较可以得到实验结果与理论结果符合得很好。 B 相位噪声测量装置
我们利用鉴频器的方法测量OEO的相位噪声,实验装置如图6(b)所示。这种方法的优点是不需要参考频率,因此可以测量任意振荡频率的相位噪声。实验中用到微波混频器,我们对OEO点端口输出的信号和光端口输出的信号经过延迟后进行比较。延迟线的长度非常重要,因为延迟线越长能够精确地测量频偏越小的相位噪声。另一方面,延迟线如果非常长精确测量相位噪声的频偏容忍度越大。在我们实验中用到的延迟是1Km或者5uS。因为这个延迟,OEO的任意频率在混频器的输出端都引起电压的波动。我们用一个具有高动态量程范围的光谱分析仪测量电压波动的光谱,并把光谱数据输入电脑。最后我们利用参考文献30中给的规则把这些信息转换成相位噪声谱。在这个实验中射频放大器的噪声系数是7dB。
C 频偏和环延迟
图7(a)是频偏 处的相位噪声,每一条曲线得到的是不同环延迟时间的噪声。很清楚,相位噪声由20dB的下降,与公式(29b)符合得很好。
图7(b)是测量偏离中心频率处30KHz处相位噪声关于环延迟时间的曲线,是从图7(a)中提取得到的。因为增加环延迟是靠增加一段光纤来实现的,振荡器的开环增益随着环的增长而减小,因为随着环的增加会引起能量的减小。由图9可以得到光电振荡器的相位噪声随着振荡功率的增加线性减小。
D 相位噪声与频率无关
为了验证光电振荡器的相位噪声与频率没有关系,我们测量相位噪声随着频率的变化情况,测量结果如图8(a)所示。在实验中我们保持环延迟时间0.28uS不变,通过改变射频滤波器来选择不同的振荡频率。由图8(a)可以得到100,300,700和800MHz的相位噪声图都重合的很好,和理论结果完全符合。图8(b)是各种不同频率频偏10KHz处的相位噪声,结果表明是一条平坦的水平线,与倍频法产生的高频信号截然不同。这个结果非常重要,这表明利用OEO可以产生高频信号,频率超过75GHz,而且相位噪声远低于倍频法产生的信号。
E 相位噪声是振荡功率的函数
我们还得到了相位噪声随着振荡功率变化得情况,如图9所示。在这个实验中OEO环的延迟时间设定在0.06uS,射频放大器的噪声系数是7dB,振荡功率数着光电流的改变而变换,更具公式(3)、(4)和(17)改变光电流。前面公式(24)和(25)说明OEO的相位噪声与振荡功率成反比。如果放大器的增益保持常数不变,而且光电流做够低从而使得热噪声成为噪声的主要成分。图9(a)中每一条曲线是在一个振荡功率下对应的相位噪声曲线,图9(b)是公式(29b)对应的曲线。图9(c)是OEO在频偏10KHz处相位噪声随着振荡功率变化得曲线,是从图9(b)中提取出来的。这些结果都很好地验证了公式29(b).
总结:
我们介绍了一种高频,高稳定性,高谱纯度,频率调谐范围宽的光电振荡器。这个稳定度高,光谱纯的光电振荡器是靠低损耗的长光纤能量储存来实现的。由于光纤对任意频率的损耗都很小,所以无论高频还是低频在光纤内的存储时间和光谱纯度是相同的。光电振荡器的振荡频率只受到调制器的调制频率的限制,目前调制频率可以达到75GHz。另一个优点是,光电振荡器除了可以直接输出微波信号,还可以输出调制的光信号,可以用于光学系统。我们同时得到的振荡器的阈值(公式5),振荡幅度(公式17)和振荡频率(公式18)的表达式。这些结果与实验中通过光电振荡器得到的结果相吻合。
由公式(24)表明光电振荡器得到的光谱是洛伦兹型的。公式(26)得知谱宽与环延迟时间的平方成反比关系。并且,在光泵浦低的情况下,热噪声占主要地位的情况下谱线宽度与振荡功率成正比关系,与Schawlow–Townes公式描述的激光器的谱宽很相似。振荡功率随着光泵浦的增加而增加,光谱谱线随着光泵浦的增大而减小。另一方面,当光泵浦比较强,激光器的相对亮度噪声占主要地位的情况下。激光器的光谱宽度就与激光器的相对亮度噪声有关,如公司(24)和(32),并且通过实验对理论进行验证。
非常重要的一点,在进行分析的过程中光电振荡器中用到的是马赫曾德尔电光调制器。其它调制器,如电吸收调制器,半导体激光器直接调制等也可以用同样的方法进行分析,只要对理论模型进行一下修改就可以。最要是对描述马赫曾德尔调制器的传输特性的方程(1)进行修改。其它方程可以用同样的方法得到。
由于独特的性能,光电振荡器有多种应用。作为压控振荡器,他可以胜任所有压控振荡器的工作,包括产生、跟踪、清除射频载波的光电领域,能够放大注入信号,可应用于高频信号载波再生和信号放大。光电振荡器还具有许多潜在的用途,包括高速时钟恢复,梳妆波和脉冲发射器,高速倍频,光子射频系统的上下变频等领域。
 爱华网
爱华网