复利与年金
1、复利
所谓复利也称利上加利,是指一笔存款或者投资获得回报之后,再连本带利进行新一轮投资的方法,在每经过一个计息期后,都要将所剩利息加入本金,以计算下期的利息。
复利的计算公式:F=P*(1+i)^n i—计息周期复利率;n—计息周期数;(1+i)^n成为一次支付终值系数,可通过复利终值系数表查得。
【1】复利现值(即现在的资金价值或本金,Present Value)是指在计算复利的情况下,要达到未来某一特定的资金金额,现在必须投入的本金。或,指资金发生在(或折算为)某一特定时间序列起点时的价值; P—现值,
【2】复利终值复利终值是指本金在约定的期限内获得利息后,将利息加入本金再计利息,逐期滚算到约定期末的本金之和。
F—终值,指资金发生在(或折算为)某一特定时间序列终点时的价值;
例:
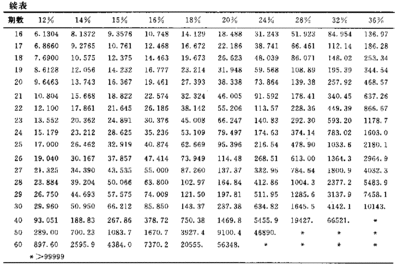
例如:本金为50000元,利率或者投资回报率为8%,投资年限为10年,那么,10年后所得到的本利和,F=50000×(1+8%)^10=50000*2.1589(查表得)=107945
由于,通胀率和利率密切关联,就像是一个硬币的正反两面,所以,复利终值的计算公式也可以用以计算某一特定资金在不同年份的实际价值。只需将公式中的利率换成通胀率即可。
2、年金(支出):
年金是指等额、定期的系列支出。例如,分期付款赊购、分期偿还贷款等。 年金有普通年金、预付年金、递延年金和永续年金。
普通年金又称后付年金,是指各期期末收付的年金。普通年金现值,是指为在每期期末取得相等金额的款项,现在需要投入的金额。
预付年金是指在每期期初支付的年金。
递延年金是指第一次支付发生在第二期或第二期以后的年金。
无限期定额支付的年金,称为永续年金。现实中的存本取息,可视为永续年金的一个例子。
【1】年金现值
年金现值是指将在一定时期内按相同时间间隔在每期期末收入或支付的相等金额折算到第一期初的现值之和。
年金现值是年金终值的逆计算。
【2】普通年金终值
普通年金终值:指一定时期内,每期期末等额收入或支出的本利和,也就是将每一期的金额,按复利换算到最后一期期末的终值,然后加总,就是该年金终值。年金终值系数表示为(F/P,5%,10)。
例如:每年存款100元,年利率为10%,经过5年,年金终值,公式为:F=100* (F/P,5%,10),可查普通年金终值系数表.
三、系数之间的关系:
【1】互为倒数关系
复利终值系数×复利现值系数=1
普通年金终值系数×偿债基金系数=1
普通年金现值系数×投资回报系数=1
【2】预付年金终值(现值)系数=普通年金终值(现值)系数×(1+折现率)
【3】普通年金终值系数=(复利终值系数-1)/i
普通年金现值系数=(1-复利现值系数)/i
【4】普通年金终值系数=普通年金现值系数×复利终值系数
普通年金现值系数=普通年金终值系数×复利现值系数。
【5】偿债基金与投资回收额
简单地说,如果是已知终值求年金,则属于计算偿债基金问题;若是属于已知现值求年金,则属于计算投资回收额问题。
 爱华网
爱华网


