相遇问题基本公式
路程÷(速度和)=相遇时间
相遇时间×(速度和)=路程
甲的速度=路程÷相遇时间-乙的速度
下面三道题都是最基本类型,可以用方程也可以用算术方法解答。应用的就是上面的公式。
一、基本练习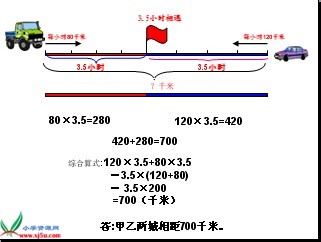
(1)甲、乙两列火车同时从相距700千米的两地相向而行,甲列车每小时行85千米,乙列车每小时行90千米,几小时两列火车相遇?
(2)两列火车从两个车站同时相向出发,甲车每小时行48千米,乙车每小时行78千米,经过2.5小时两车相遇。两个车站之间的铁路长多少千米?
(3)甲、乙两列火车同时从相距988千米的两地相向而行,经过5.2小时两车相遇。甲列车每小时行93千米,乙列车每小时行多少千米?
二、综合练习
“走路或者开车”只是相遇问题的一个基本载体,还有一些习题,看上去和“走路、开车”没什么关系,其实质也是相遇问题。事实上,两人共同完成一项工作也属于相遇问题。
有时会遇到“还相距某某千米”或者“还有某某工作没完成”这样的句子,这时候要把这部分没完成的工作从工作总量中减掉。
请看下面各题。
(1)师徒两人合作加工520个零件,师傅每小时加工30个,徒弟每小时加工20个,几小时以后还有70个零件没有加工?
(2)甲、乙两队合挖一条水渠,甲队从东往西挖,每天挖75米;乙队从西往东挖,每天比甲队少挖5米,两队合作8天挖好,这条水渠一共长多少米?
(3)甲、乙两艘轮船从相距654千米的两地相对开出而行,8小时两船还相距22千米。已知乙船每小时行42千米,甲船每小时行多少千米?
三、提高练习
还有一些练习题相对就比较难一些,其中一些条件不直接给,需要找到未知的条件与已知条件的关系。
请看下面各题
(1)一辆汽车和一辆自行车从相距172.5千米的甲、乙两地同时出发,相向而行,3小时后两车相遇。已知汽车每小时比自行车多行31.5千米,求汽车、自行车的速度各是多少?【可以用方程,设一个速度为X,再用含有X的式子表示出另一个速度,然后根据等量关系列出方程】
(2)两地相距270千米,甲、乙两列火车同时从两地相对开出,经过4小时相遇。已知甲车的速度是乙车的1.5倍,求甲、乙两列火车每小时各行多少千米??【可以用方程,设一个速度为X,再用含有X的式子表示出另一个速度,然后根据等量关系列出方程】
(3)甲、乙两城相距680千米,从甲城开往乙城的普通客车每小时行驶60千米,2小时后,快车从乙城开往甲城,每小时行80千米,快车开出几小时后两车相遇?【普通客车先出发了2小时,这两小时的路程不是两车共同走的路程,该怎么处理?】
(4)姐妹俩同时从家里到少年宫,路程全长770米。妹妹步行每分钟行60米,姐姐骑自行车以每分钟160米的速度到达少年宫后立即返回,途中与妹妹相遇。这时妹妹走了几分钟?【两人相遇时一共走了多少路程?】
(5)小明和小华从甲、乙两地同时出发,相向而行。小明步行每分钟走60米,小华骑自行车每分钟行190米,几分钟后两人在距中点650米处相遇?【在距中点650米处相遇,说明小华比小明多走了多少米?这就是他们的路程差。路程差÷(速度差)=共同行走的时间】
(6)A、B两地相距300千米,两辆汽车同时从两地出发,相向而行。各自达到目的地后又立即返回,经过8小后它们第二次相遇。已知甲车每小时行45去,千米,乙车每小时行多少千米?【二次相遇问题,画画图看看,两人二次相遇时,一共走了几个全程?】
 爱华网
爱华网



