给定一个单链表,只给出头指针h:
1、如何判断是否存在环?
2、如何知道环的长度?
3、如何找出环的连接点在哪里?
4、带环链表的长度是多少?
解法:
1、对于问题1,使用追赶的方法,设定两个指针slow、fast,从头指针开始,每次分别前进1步、2步。如存在环,则两者相遇;如不存在环,fast遇到NULL退出。
2、对于问题2,记录下问题1的碰撞点p,slow、fast从该点开始,再次碰撞所走过的操作数就是环的长度s。
3、问题3:有定理:碰撞点p到连接点的距离=头指针到连接点的距离,因此,分别从碰撞点、头指针开始走,相遇的那个点就是连接点。(证明在后面附注)
4、问题3中已经求出连接点距离头指针的长度,加上问题2中求出的环的长度,二者之和就是带环单链表的长度
void Isloop(Llink head)
{
if(!head||!head->next)
return;
Llink p,q;
bool loop=false;
p=q=head->next;
while(q&&q->next)//判断是否有环
{
p=p->next;
q=q->next->next;
if(p==q)
{
loop=true;
break;
}
}
if(!loop)
cout<<"Thislink has not loopn";
else
{
cout<<"Thislink has a loopn";
Llink r=p;
q=head->next;
intnonloop=1,loopcount=1;
//nonloop计算非环结点数,loopcount计算环上结点数
do//计算环上的结点数
{
p=p->next;
++loopcount;
}while(p!=r);
--loopcount;
while(p!=q)//得到环的入口结点,同时计算得到非环的结点数
{
p=p->next;
q=q->next;
++nonloop;
}
--nonloop;
cout<<"nStartof loop:"<<p->data<<endl;
cout<<"nCountof nonloop: "<<nonloop
<<"nCount of loop:"<<loopcount
<<"nCount of Linknode:"<<nonloop+loopcount<<endl;
}
}
判断是否存在环的程序:
boolIsExitsLoop(slist*head)- {
- slist*slow=head,*fast=head;
- while(fast&&fast->next)
- {
- slow=slow->next;
- fast=fast->next->next;
- if(slow==fast)break;
- }
- return!(fast==NULL||fast->next==NULL);
- }
寻找环连接点(入口点)的程序:
slist*FindLoopPort(slist*head)- {
- slist*slow=head,*fast=head;
- while(fast&&fast->next)
- {
- slow=slow->next;
- fast=fast->next->next;
- if(slow==fast)break;
- }
- if(fast==NULL||fast->next==NULL)
- returnNULL;
- slow=head;
- while(slow!=fast)
- {
- slow=slow->next;
- fast=fast->next;
- }
- returnslow;
- }
亦可以用类似与hash表的方法,即设立一个数组,将链表结点中的值做数组下标,当赋值冲突时就是环的接入点
- boolisloop(Llink p)
{
if(!p||!p->next)
return true;
int a[MAXSIZE],n=0;
memset(a,0,sizeof(int)*MAXSIZE);
p=p->next;
while(p)
{
if(a[p->data]==-1)//存在环时,会发生冲突
{
cout<<"nLoopnode:"<<p->data<<endl
<<"nLenof node:"<<n<<endl;
returntrue;
}
a[p->data]=-1;
++n;
p=p->next;
}
return false;
}
Llink CreatlinkLoop() - //创建一个有环的链表
{
Llink head=new Lnode;
//head->data=0;
head->next=NULL;
Lelemtype e;
Llink q=head;
int N=0;
cout<<"inputelems:";
while(cin>>e)
{
Llink p=new Lnode;
++N;
p->data=e;
p->next=q->next;
q->next=p;
q=p;
}
cin.clear();
cin.sync();
srand(time(0));
q->next=Findnode(head,rand()%N);//随机产生环的接入点
return head;
}
Llink Findnode(Llink head,int n)//找出链表中的第n个结点
{
if(n<=0)
return head;
Llink p=head->next;
for(inti=1;p&&i<n;++i)
p=p->next;
return p;
}
////////////////////////////////////////////////////////
附注
问题2的证明如下:
链表形状类似数字 6 。
假设甩尾(在环外)长度为 a(结点个数),环内长度为 b 。
则总长度(也是总结点数)为 a+b 。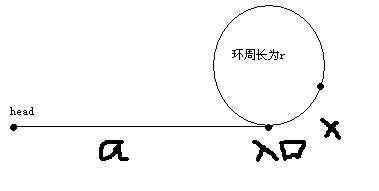
从头开始,0 base 编号。
将第 i 步访问的结点用 S(i) 表示。i = 0, 1 ...
当 i<a 时,S(i)=i ;
当 i≥a 时,S(i)=a+(i-a)%b 。
分析追赶过程:
两个指针分别前进,假定经过 x 步后,碰撞。则有:S(x)=S(2x)
由环的周期性有:2x=tb+x 。得到 x=tb 。
另,碰撞时,必须在环内,不可能在甩尾段,有 x>=a 。
连接点为从起点走 a 步,即 S(a)。
S(a) = S(tb+a) = S(x+a)。
得到结论:从碰撞点 x 前进 a 步即为连接点。
根据假设易知 S(a-1) 在甩尾段,S(a) 在环上,而S(x+a) 必然在环上。所以可以发生碰撞。
而,同为前进 a 步,同为连接点,所以必然发生碰撞。
综上,从 x点和从起点同步前进,第一个碰撞点就是连接点。
/////////////////////////////////////////////////////////////
假设单链表的总长度为L,头结点到环入口的距离为a,环入口到快慢指针相遇的结点距离为x,环的长度为r,慢指针总共走了s步,则快指针走了2s步。另外,快指针要追上慢指针的话快指针至少要在环里面转了一圈多(假设转了n圈加x的距离),得到以下关系:
s = a + x;
2s = a + nr + x;
=>a + x = nr;
=>a = nr - x;
由上式可知:若在头结点和相遇结点分别设一指针,同步(单步)前进,则最后一定相遇在环入口结点,搞掂!
附图:
 爱华网
爱华网