问一个基本的问题。
负数在计算机中如何表示?
举例来说,+8在计算机中表示为二进制的1000,那么-8怎么表示呢?
很容易想到,可以将一个二进制位(bit)专门规定为符号位,它等于0时就表示正数,等于1时就表示负数。比如,在8位机中,规定每个字节的最高位为符号位。那么,+8就是00001000,而-8则是10001000。
但是,随便找一本《计算机原理》,都会告诉你,实际上,计算机内部采用2的补码(Two's Complement)表示负数。
什么是2的补码?
它是一种数值的转换方法,要分二步完成:
第一步,每一个二进制位都取相反值,0变成1,1变成0。比如,00001000的相反值就是11110111。
第二步,将上一步得到的值加1。11110111就变成11111000。
所以,00001000的2的补码就是11111000。也就是说,-8在计算机(8位机)中就是用11111000表示。
不知道你怎么看,反正我觉得很奇怪,为什么要采用这么麻烦的方式表示负数,更直觉的方式难道不好吗?
昨天,我在一本书里又看到了这个问题,然后就花了一点时间到网上找资料,现在总算彻底搞明白了。
2的补码的好处
首先,要明确一点。计算机内部用什么方式表示负数,其实是无所谓的。只要能够保持一一对应的关系,就可以用任意方式表示负数。所以,既然可以任意选择,那么理应选择一种最方便的方式。
2的补码就是最方便的方式。它的便利体现在,所有的加法运算可以使用同一种电路完成。
还是以-8作为例子。
假定有两种表示方法。一种是直觉表示法,即10001000;另一种是2的补码表示法,即11111000。请问哪一种表示法在加法运算中更方便?
随便写一个计算式,16 + (-8) = ?
16的二进制表示是 00010000,所以用直觉表示法,加法就要写成:
00010000
+10001000
---------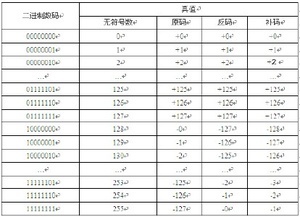
10011000
可以看到,如果按照正常的加法规则,就会得到10011000的结果,转成十进制就是-24。显然,这是错误的答案。也就是说,在这种情况下,正常的加法规则不适用于正数与负数的加法,因此必须制定两套运算规则,一套用于正数加正数,还有一套用于正数加负数。从电路上说,就是必须为加法运算做两种电路。
现在,再来看2的补码表示法。
00010000
+11111000
---------
100001000
可以看到,按照正常的加法规则,得到的结果是100001000。注意,这是一个9位的二进制数。我们已经假定这是一台8位机,因此最高的第9位是一个溢出位,会被自动舍去。所以,结果就变成了00001000,转成十进制正好是8,也就是16+ (-8)的正确答案。这说明了,2的补码表示法可以将加法运算规则,扩展到整个整数集,从而用一套电路就可以实现全部整数的加法。
2的补码的本质
在回答2的补码为什么能正确实现加法运算之前,我们先看看它的本质,也就是那两个步骤的转换方法是怎么来的。
要将正数转成对应的负数,其实只要用0减去这个数就可以了。比如,-8其实就是0-8。
已知8的二进制是00001000,-8就可以用下面的式子求出:
00000000
-00001000
---------
因为00000000(被减数)小于0000100(减数),所以不够减。请回忆一下小学算术,如果被减数的某一位小于减数,我们怎么办?很简单,问上一位借1就可以了。
所以,0000000也问上一位借了1,也就是说,被减数其实是100000000,算式也就改写成:
100000000
-00001000
---------
11111000
进一步观察,可以发现100000000 = 11111111 + 1,所以上面的式子可以拆成两个:
11111111
-00001000
---------
11110111
+00000001
---------
11111000
2的补码的两个转换步骤就是这么来的。
为什么正数加法适用于2的补码?
实际上,我们要证明的是,X-Y或X+(-Y)可以用X加上Y的2的补码完成。
Y的2的补码等于(11111111-Y)+1。所以,X加上Y的2的补码,就等于:
X + (11111111-Y) + 1
我们假定这个算式的结果等于Z,即 Z = X + (11111111-Y) + 1
接下来,分成两种情况讨论。
第一种情况,如果X小于Y,那么Z是一个负数。这时,我们就对Z采用2的补码的逆运算,求出它对应的正数绝对值,再在前面加上负号就行了。所以,
Z = -[11111111-(Z-1)] = -[11111111-(X + (11111111-Y) + 1-1)] = X- Y
第二种情况,如果X大于Y,这意味着Z肯定大于11111111,但是我们规定了这是8位机,最高的第9位是溢出位,必须被舍去,这相当于减去100000000。所以,
Z = Z - 100000000 = X + (11111111-Y) + 1 - 100000000 = X - Y
这就证明了,在正常的加法规则下,可以利用2的补码得到正数与负数相加的正确结果。换言之,计算机只要部署加法电路和补码电路,就可以完成所有整数的加法。
(原文完)
读记:
当我看到上面最后那段证明正数加法适用于2的补码的时候,我产生了一个疑问:作者是怎么想到要从两种情况来进行讨论的呢?不分情况讨论不行吗?
我的想法比较单纯:
直接将Z写成:Z = X + (11111111-Y) + 1 = X- Y +(11111111 + 1) = X - Y + 100000000;
因为我们假定是在八位机上完成这次补码加法计算,那么如果第九位为1的话,肯定要被丢弃的,实际上计算机的结果是将纸面得到的X-Y+100000000的结果上减去100000000,则
最后结果是 Z = X - Y + 100000000 - 100000000 = X -Y。
至此,便完成了全部的证明。
不过,原文作者的证明给我了一些启示:
证明从两种不同的情况,用了两种不同的处理方法来求得同一个结果Z=X-Y。可见Z是恒等于X-Y的,并不取决于我们对X-Y结果是正是负的判断。也就是说,正与负已经被统一起来了,不必再区分,也不能区分。
我们学谭浩强的C语言程序设计的时候,书中说正数的补码就是原码,负数的补码如前所述处理。统一格式的好处是能够简化硬件电路的实现(因为加减法统一),但如果没有给数字添加符号位,就无从知晓到底一个数是正数还是负数。进一步的问题是,即使我们给预留了符号位,但是如文中所述,符号位并没有参与计算过程,那么得到的结果是正数还是负数,我们又是如何得知呢?
借着这个问题,我们可以得以思考无符号与有符号整型数的区别及高级语言中对有符号运算的实现。
现在,我们就来分析一下这个问题。
---------------------------------------------------------------------------------------
让我把问题提炼一下:求 Z = X+ (-Y). 已知 X、Y>=0,问如何确定Z的符号位?
约定数字的表示为:符号位,8位数补码形式
结论:正+负 符号位可以参加运算,利用溢出特性,可以得到正确的结果。
正+正 符号位不可参加运算,因为一旦溢出,则会得到错误的符号位结果。
P.S.
减法有以下几种情况:
正-正:
正-负:正+正
负-负:其实还是正-负
---------------------------------
能不能将Z=X-Y,X、Y为任意情况的通用处理过程描述出来?
换句话说,能不能将结论推广到X、Y喂任意情况?
 爱华网
爱华网