线性代数一:二阶和三阶行列式
对于初中所学的二元线性方程组,我们可以通过加减法或者是消元法得出结果。运用消元法消去方程组中的未知数,就可以得到二元线性方程组的解。但是我们可以编造一套算法来简化这种计算,即把每个二元线性方程标准化后,将未知数前的系数排成二行二列的系数行列式,行列式中的每个数称为它的元素,横排叫做行,竖排叫做列,元素的第一个指标和第二个指标分别依次表示行数和列数。若要求解其中的未知数可以用方程组的常数列替换掉系数行列式中的该未知数前的系数,并用替换掉的行列式比上系数行列式就可以得出未知数。这种方法也就是n元线性方程组的克拉默法则。
对于三元线性方程组和n元线性方程组都可以用上诉的克拉默法则进行计算。但是克拉默法则的适用条件只能是n个方程的n元方程组,并且用这种方法如果没有辅助编程的话,需要计算n+1个行列式,计算量特别地大。不过行列式还有其自身的其他运用。本人一向不推崇克拉默法则。方程组的各种解法中,高斯消元法、改进后的高斯若当消元法(这两种方法以后介绍)还是比较适用的方法,无论是手工运算还是编写算法程序都会很简单的。
行列式的计算方法很多,比如:最不实用的定义法,行列式的性质转化法,按行列展开的代数余子式法,拉普拉斯展开定理等,不过二三阶的行列式可以用对角线法则,行列式按行(列)展开法,这些方法还是比较容易掌握的。先声眀注意:对角线法则只适用二三阶行列式,对于四阶及四阶以上的行列式就不在适用,原因详见行列式的逆序定义。
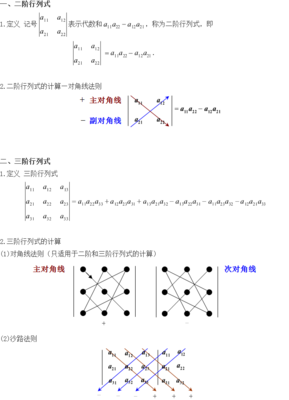
对角线法则:二三阶行列式的值等于主对角线乘积之和与副对角线乘积之和的差值。对于二阶行列式,主对角线元素就是从左上角到右下角的直线,副对角线元素就是从右上角到左下角的直线。对于三阶行列式,主对角线和副对角线的连线规则同二阶行列式,不过与三阶行列式平行的主对角线和副对角线上的元素也可以看做是对应的性质的数,即之前的正负号与主副对角线相同。(叙述有点罗嗦,计算方法可以看教材中的图例)。
展开定理:任何行列式可以转化为比它低一阶的行列式后进行计算。展开的法则在以后介绍展开定理时详细介绍。三阶行列式可以按第一行展开为第一行的每一个元素与消除这元素所在行列后的行列式的乘积的代数和。其代数和每项的正负号由哪一个元素的所在行列之和决定。行列之和为偶数则为正,行列之和为负数则为负。行列式只可按其中任一行或任一列展开,挑选标准以方便计算为原则,尤其含零行列多的可以计算非常简便。行列式展开式不可按每一行展开后求其和,这样的结果是原来值得阶数倍。
一般教材接下来会介绍行列式的一般知识,不过我认为行列式只是一种工具,而二三阶行列式的知识足可以适用于高等数学,矢量分析等课程。而线性代数是研究线性规律的一门学科,其理论核心是线性方程组理论,研究的工具是矩阵,行列式,向量,使用的观点是秩和特征值,基本方法是初等变换法。接下来我会总结矩阵的基本知识,因为矩阵的观点更为基本。在介绍完矩阵后直接用方阵来定义行列式,而后系统介绍行列式的理论知识。
 爱华网
爱华网



