PB05000821 吴瑞阳
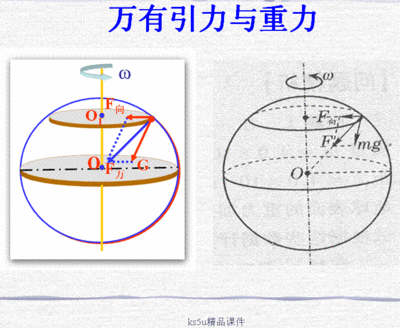
万有引力定律的发现
我们大家都知道万有引力定律是牛顿发现的,小时候我们也听说过牛顿看到苹果落地而发现万有引力的故事。但它的发现岂只是看见苹果落地这么简单?
万有引力公式: 其中G为万有引力常量。在牛顿的时代,一些科学家已经有了万事万物都有引力的想法。而且牛顿和胡克曾经为了万有引力的发现权发生过争论。有资料表明,万有引力概念由胡克最先提出,但由于胡克在数学方面的造诣远不如牛顿,不能解释行星的椭圆轨道,而牛顿不仅提出了万有引力和距离的平方成正比,而且圆满的解决了行星的椭圆轨道问题,万有引力的优先发现权自然归属牛顿。
正如他所说过,牛顿是站在巨人的肩膀上。开普勒的研究成果对万有引力的发现有着不可磨灭的贡献。开普勒是德意志的天文学家,他的老师弟谷把一生的天文观测资料留给了他。在此基础上,开普勒经过20年的计算和整理于1609年发表了行星运动的第一、第二定律。后来又发表了行星运动的第三定律。
在牛顿的回忆录里可知,牛顿最先研究的是月亮的运动。牛顿的平方反比律是由开普勒的行星运动第三定律得出的。要对椭圆轨道情况进行计算,显然牛顿还必须有一些关于微积分和基本力学定律的概念,牛顿在基础力学上有过众多发现,同时牛顿和莱布尼茨各自独立的发现了微积分。牛顿应用了微积分来计算万有引力。关于万有引力定律的发现权,历史的结论是:它是牛顿发现的。万有引力的表达式为 ,它的建立是牛顿定律和开普勒定律的综合的结果,而牛顿在其中起了关键的作用。
万有引力定律的建立
一.平方反比律的确定
1.从理论计算得出平方反比的假设:
为了简便起见,可把行星运动轨道看作圆形(把行星轨道看作圆形时,课本上已有相关证明),这样,根据面积定律,行星应作匀速圆周运动,只有向心加速度a=v2/r,其中,v是行星运行速度,r是圆形轨道的半径。
根据牛顿第二定律: f=ma
有
又由
由开普勒第三定律 ,K是与行星无关的太阳常量
即
于是 ……①
牛顿得到第一个结果:如果太阳的引力是行星运动的原因,则这种力应和行星到太阳的距离的平方成反比。
2.平方反比假设的验证:
牛顿“苹果落地”的故事广为流传。故事大意是说,1665-1666年感染病流行,牛顿从剑桥大学退职在家,一天,他在花园里想重力的动力学问题,偶然看到苹果落地,引起他的思考。在我们能够攀登的最远距离上和最高山颠上,都未发现重力有明显的减弱,这个力必然到达比通常想象的远得多的地方。那也应该高到月球上。如果是这样,月球的运动必定受它的影响,或许月球就是由于这个原因,才保持在它的轨道上的。
A
B
P
O
θ
r
s
设想月球处在它的轨道上的任意点A(见图),O是地心,如果不受外力,它将沿一直线AB运动,然而实际它的轨道是弧线AP,AB与轨道在A点相切。则月球向O落下了距离BP=y , 令弧长AP=s=2πrt/T ,
而 cosθ≈1- /2, θ=s/r
则 y=r (1-cosθ)≈s2/2r =4π2r2t2/2rT2=2π2rt2/T2,
在地面上t时间内一个重物下落距离为
y=gt2/2
由此得
y/y’ =4π2r/gT2
月球绕地的周期T=27.3d ≈2.36×106 s,地面上的重力加速度g=9.8 m/s2,地球半径R的准确数值是6400km,古希腊的天文学家伊巴谷通过观测月全食持续的时间,曾相当精确的估算出地月距离r为地球半径的60倍,则r=60 R=3.84×105km用这个数值代入,即得
y/y’ =1/3600
而 R2/r2=1/3600
y/y’=a/g=ma/mg=f/mg= R2/r2
所以: f=mg R2/r2 即:力和距离的平方成反比
二.与m和M成正比的确定
①式表明力与被吸引物体质量m成正比,同时根据牛顿第三定律,力的作用是相互的,f是M对m的作用,f’是m对M的作用,f与m成正比,则同理f’必与M成正比,又f =f’,则f必同时与m和M成正比。①式可写成:
f=GMm/r2, ……②
其中G是万有引力常量。
三.万有引力常量的G测定
既然有了万有引力的表达式,那就要测出万有引力常量。测量万有引力常量G的数值,就要测量两个已知质量的物体间的引力。1798年,卡文迪许(H.Cavendish)做了第一个精确的测量。
他所用的是扭秤装置,如图所示,两个质量均为m的小球固定在一根轻杆的两端,在用一根石英细丝将这两杆水平的悬挂起来,每个质量为m的小球附近各放置一个质量为M的大球。根据万有引力定律,当大球在位置AA时,由于小球受到吸引力,悬杆因受到一个力矩而转动,使悬丝扭转。引力力矩最后被悬丝的弹性恢复力矩所平衡。悬丝扭转的角度θ可用镜尺系统来测定。为了提高测量的灵敏度,还可以将大球放在位置BB,向相反的方向吸引小球。这样,两次悬杆平衡之间的夹角纠正大了一倍。如果已知大球和小球的质量M,m和他们相隔的距离,以及悬丝扭力的相关系数,就可由测得的θ来计算G。卡文迪许测定的万有引力常量值为:
G=6.754×10-11m3/kg·s2。万有引力常量是目前测得最不精确的一个基本物理常量,因为引力太弱,又不能屏蔽它的干扰,实验很难做。从卡文迪许到现在已近200年,许多人用相同或不同的方法测量G的数值,不断地改进其精度。国际科学联盟理事会科技数据委员会(CODATA)1986年推荐的数值为
G=6.67259(85)×10-11 m3/kg·s2,
不确定度为128/1000000(即万分之1.28)。
万有引力实验演示
一,实验现象:
一些科技博物馆里又如图的演示装置: 一个类似碗状,但是碗壁向内拱入的圆盘。一个粘有油墨的小球以较低速度从圆盘边缘进入,在圆盘上绕中心滚动并留下痕迹。可以观察到,随着时间变化,小球的速度越来越快,到最后掉入中间的小洞。而且越到中间小球的半径变化越缓慢(也就是说小球的轨迹在中间是最密集)。小球的轨迹并不是正圆的,而是一种半径越来越小的圆弧。(如果两个小球先后进入盘中则会有角位移前后追赶的现象。)
二,原理解释:
1,为什么用它来演示万有引力定律
由万有引力定律的表达式可以推知,行星势能为
O
r
h
而实验中用重力势能来代替万有引力势能mgh= -GMm/r
所以只要满足h=-GM/gr则可以用重力势能来代替万有引力势能。
同时r表示物体间的距离。当图示曲线绕h轴旋转后便会形成实验中所用到的曲面,当曲线如图时:dh/dr=GM/gr2,
f=mgtanθ=mgdh/dr=mgGM/gr2=GMm/r2
所以不论从能量还是从力的角度来讲,这个实验模型可以模拟演示万有引力。
2,为什么小球会越来越快
由离心力f=mv2/r=F知,动能为E k=1/2mV2=1/2GMm/r,由公式可见,r越小动能越大,自然速度会越快。
3,为什么小球到中间轨迹密集
这是一个有耗散力做工的系统,在旋转的时候摩擦力做功发热耗散掉一部分能量w= ,而f的大小只与接触的压力和摩擦系数有关系,在距离为r处的摩擦力转一周做功为:w= =2πrmgμcos[arctan(dh/dr)]=
又:dE/dr= GMm/r2,可见在r越大的时候,势能的变化越慢,故在外圈时,变化一个小量dr后势能的变化不如内圈的大,而转一圈消耗能量却比内圈大。所以在里圈旋转时,转动位置每下降一小段,可供小球旋转的能量就较多,而小球每转一圈摩擦力消耗能量较少,故小球在同样的一小段距离上会比外边多转几圈。
4,小球的轨迹为何是一个不断向里缩进的圆弧
如果盘面足够光滑,即没有摩擦力做功,则小球的轨迹会是什么样的呢?
A,小球在进入圆盘边缘时恰好获得的动能足够在盘的边缘运动所需的动能:
mgh=1/2 mv2 即:F=mv2/r则小球会沿着圆盘边缘做正圆轨迹的运动
B,小球在进入圆盘边缘时未达到在圆盘的边缘运动所需的动能:
Mgh〉1/2mv2,F> mv2/r则小球会做正圆轨迹的运动同时径向有一个分运动(缩小半径把势能转化为动能直到满足平衡为止)到某一半径时会达到F=mv2/r在此处做正圆运动
C,小球在进入圆盘边缘时的动能超过在盘的边缘运动所需的动能:
Mgh<1/2mv2,F<mv2/r体现在圆盘上的力学分析为则小球会沿着边缘飞出
实验中模拟的只是B情况。
下面再考虑摩擦力:
由于摩擦力作负功,在运动过程中,小球的动能在不断损失,这就要求小球能不断的缩小半径来寻找新的平衡,直到最后半经过小、能量不足而掉入中间的小孔
因此就有:小球的轨迹是一个不断向里缩进的圆
5,两个小球为什么会有角度相互追赶?
由万有引力公式知:角速度ω= ,故半径越小,角速度越大。先后进入的两个小球的角速度总是先进入的大于后进入的,所以在一段时间里总是前面的小球转过的角度比后面的多,因此角度差一直在增大,先进入的球会超过后进入的球多圈,所以看上去总是两个小球一会儿这个在前,一会儿另一个在前,相互追逐。
万有引力的应用
万有引力定律作为一个自然界最基本的定律,无论是在理论研究还是工程设计等各种时候都有着极其广泛的应用。比如航天中,航天器与天体接近时的万有引力可以作为一种有效的加速办法(弹弓效应);宇宙物理中常常以测定天体的万有引力产生的效应来断定天体的位置和质量;在电磁探测受局限的地域,可以通过万有引力的测量计算,来探知地下的物质 密度,从而断定地下矿藏的分布或是地下墓穴的规模和位置;在另外一些领域,比如精密工业中的超圆滚球体的制造,可以选择在太空生产,因为那里有理想的受力环境(因为在宇宙飞船上物体处于失重状态,而又由宇宙大尺度分布的均匀性,其他星体的引力又可以忽略不计);以研究生物在太空无重力(亦即万有引力语离心力平衡抵消)为对象的项目已经发展成一门高新前沿的科技。如果将蔬菜水果种子带到太空中,在无重力环境与宇宙射线的影响下,有些变异品种的品质与地球上的品种相比大大提高。
事实上,万有引力定律常常是理论研究的最基本最常用的公式之一。以下就举一个实际应用的例子来说明这一点。
人造卫星的发射过程:
1,当我们要发射一颗地球卫星是我们只要以一定的角度和一定的初速度把卫星发射向太空,这个速度的理论值由万有引力定律可推知为:7.9km/s。万有引力定律给我们确定了卫星上天的边界条件。当然实际发射中还要去考虑阻力问题,并且不是瞬间加速到此值,是一个渐加速过程,这就是较复杂的了。
2,当我们要求卫星成为一个太阳的卫星时,我们的发射速度的理论值会高达11.2km/s。同样实际过程中速度也不会达到此值,而是渐加速渐升高。
3,当我们要求卫星成为一个太阳外的天体时,我们的发射速度的理论值会高达16.7km/s。实际过程中速度也不会达到此值,事实上我们还故意把飞行器发射到太阳系天体的附近,利用飞行器和天体间的万有引力,应用弹弓效应来改变飞行器的速度和方向。
从以上的应用中可以看出万有引力的重要地位。万有引力的概念在刚被提出的时候曾引起了一次“科学革命”。在随后的那个时代里,因此而引发了研究探索宇宙的热潮,产生了许多新的学科及项目,并有了众多新的发现。这些研究成果至今仍与我们的生活息息相关。万有引力定律的发现推动了整个人类文明的进程,是人类在认识宇宙的道路上迈出的一大步,也是极其重要的一步!
我们更有理由相信,万有引力在将来的科学探索研究中仍然会发挥相当重要的作用。
 爱华网
爱华网