股票定价模型
-、零增长模型
零增长模型假定股利增长率等于零,即G=0,也就是说未来的股利按一个固定数量支付。
[例]
假定某公司在未来无限时期支付的每股股利为8元,其公司的必要收益率为10%,可知一股该公司股票的价值为8/0.10=80元,而当时一股股票价格为65元,每股股票净现值为80—65=15元,因此该股股票被低估15元,因此建议可以购买该种股票。
[应用]
零增长模型的应用似乎受到相当的限制,毕竟假定对某一种股票永远支付固定的股利是不合理的。但在特定的情况下,在决定普通股票的价值时,这种模型也是相当有用的,尤其是在决定优先股的内在价值时。因为大多数优先股支付的股利不会因每股收益的变化而发生改变,而且由于优先股没有固定的生命期,预期支付显然是能永远进行下去的。
二、不变增长模型
(1)一般形式。如果我们假设股利永远按不变的增长率增长,那么就会建立不变增长模型。
[例]假如去年某公司支付每股股利为1.80元,预计在未来日子里该公司股票的股利按每年5%的速率增长。因此,预期下一年股利为1.80×(1十0.05)=1.89元。假定必要收益率是11%,该公司的股票等于1.80×[(1十0.05)/(0.11—0.05)]=1.89/(0.11—0.05)=31.50元。而当今每股股票价格是40元,因此,股票被高估8.50元,建议当前持有该股票的投资者出售该股票。
(2)与零增长模型的关系。零增长模型实际上是不变增长模型的一个特例。特别是,假定增长率合等于零,股利将永远按固定数量支付,这时,不变增长模型就是零增长模型。
从这两种模型来看,虽然不变增长的假设比零增长的假设有较小的应用限制,但在许多情况下仍然被认为是不现实的。但是,不变增长模型却是多元增长模型的基础,因此这种模型极为重要。
三、多元增长模型
多元增长模型是最普遍被用来确定普通股票内在价值的贴现现金流模型。这一模型假设股利的变动在一段时间7、内并没有特定的模式可以预测,在此段时间以后,股利按不变增长模型进行变动。因此,股利流可以分为两个部分。
第一部分包括在股利无规则变化时期的所有预期股利的现值。
第二部分包括从时点T来看的股利不变增长率变动时期的所有预期股利的现值。因此,该种股票在时间点的价值(VT)可通过不变增长模型的方程求出
[例]假定A公司上年支付的每股股利为0.75元,下一年预期支付的每股票利为2元,因而再下一年预期支付的每股股利为3元,即
从T=2时,预期在未来无限时期,股利按每年10%的速度增长,即0:,Dz(1十0.10)=3×1.1=3.3元。假定该公司的必要收益率为15%,可按下面式子分别计算V7—和认t。该价格与目前每股股票价格55元相比较,似乎股票的定价相当公平,即该股票没有被错误定价。
(2)内部收益率。零增长模型和不变增长模型都有一个简单的关于内部收益率的公式,而对于多元增长模型而言,不可能得到如此简捷的表达式。虽然我们不能得到一个简捷的内部收益率的表达式,但是仍可以运用试错方法,计算出多元增长模型的内部收益率。即在建立方程之后,代入一个假定的伊后,如果方程右边的值大于P,说明假定的P太大;相反,如果代入一个选定的尽值,方程右边的值小于认说明选定的P太小。继续试选尽,最终能程式等式成立的尽。
按照这种试错方法,我们可以得出A公司股票的内部收益率是14.9%。把给定的必要收益15%和该近似的内部收益率14.9%相比较,可知,该公司股票的定价相当公平。
(3)两元模型和三元模型。有时投资者会使用二元模型和三元模型。二元模型假定在时间了以前存在一个公的不变增长速度,在时间7、以后,假定有另一个不变增长速度城。三元模型假定在工时间前,不变增长速度为身I,在71和72时间之间,不变增长速度为期,在72时间以后,不变增长速度为期。设VTl表示
在最后一个增长速度开始后的所有股利的现值,认-表示这以前所有股利的现值,可知这些模型实际上是多元增长模型的特例。
四、市盈率估价方法
市盈率,又称价格收益比率,它是每股价格与每股收益之间的比率,其计算公式为反之,每股价格=市盈率×每股收益
如果我们能分别估计出股票的市盈率和每股收益,那么我们就能间接地由此公式估计出股票价格。这种评价股票价格的方法,就是“市盈率估价方法”。
五、贴现现金流模型
贴现现金流模型是运用收入的资本化定价方法来决定普通股票的内在价值的。按照收入的资本化定价方法,任何资产的内在价值是由拥有这种资产的投资者在未来时期中所接受的现金流决定的。由于现金流是未来时期的预期值,因此必须按照一定的贴现率返还成现值,也就是说,一种资产的内在价值等于预期现金流的贴现值。对于股票来说,这种预期的现金流即在未来时期预期支付的股利,因此,贴现现金流模型的公式为
式中:Dt为在时间T内与某一特定普通股相联系的预期的现金流,即在未来时期以现金形式表示的每股股票的股利;K为在一定风险程度下现金流的合适的贴现率;V为股票的内在价值。
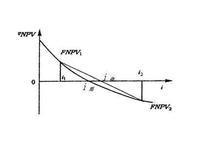
在这个方程里,假定在所有时期内,贴现率都是一样的。由该方程我们可以引出净现值这个概念。净现值等于内在价值与成本之差,即
式中:P为在t=0时购买股票的成本。
如果NPV>0,意味着所有预期的现金流入的净现值之和大于投资成本,即这种股票被低估价格,因此购买这种股票可行;
如果NPV<0,意味着所有预期的现金流入的净现值之和小于投资成本,即这种股票被高估价格,因此不可购买这种股票。
在了解了净现值之后,我们便可引出内部收益率这个概念。内部收益率就是使投资净现值等于零的贴现率。如果用K*代表内部收益率,通过方程可得
由方程可以解出内部收益率K*。把K*与具有同等风险水平的股票的必要收益率(用K表示)相比较:如果K*>K,则可以购买这种股票;如果K*<K,则不要购买这种股票。
一股普通股票的内在价值时存在着一个麻烦问题,即投资者必须预测所有未来时期支付的股利。由于普通股票没有一个固守的生命周期,因此建议使用无限时期的股利流,这就需要加上一些假定。
这些假定始终围绕着胜利增长率,一般来说,在时点T,每股股利被看成是在时刻T—1时的每股股利乘上胜利增长率GT,其计
例如,如果预期在T=3时每股股利是4美元,在T=4时每股股利是4.2美元,那么不同类型的贴现现金流模型反映了不同的股利增长率的假定。
六、开放式基金的价格决定
开放式基金由于经常不断地按客户要求购回或者卖出自己公司的股份,因此,开放式基金的价格分为两种,即申购价格和赎回价格。
1.申购价格
开放式基金由于负有在中途购回股票的义务,所以它的股票‘般不进入股票市场流通买卖,而是主要在场外进行,投资者在购入开放式基金股票时,除了支付资产净值之外,还要支付一定的销售附加费用。也就是说,开放公司股票的申购价格包括资产净值和弥补发行成本的销售费用,该附加费一般保持在4%一9%的水平上,通常为8.5%,并且在投资者大量购买时,可给予一定的优惠。开放式基金的申购价格、资产净值和附加费之间的关系可用下式表示。
例如;某开放式基金的资产净值为10元,其附加费为8%,则其申购价格为10/(1?%)=10.87元。
但是,对于一般投资者来说,该附加费是一笔不小的成本,增加了投资者的风险,因此;出现了一些不计费的开放式基金,其销售价格直接等于资产净值,投资者在购买该种基金时,不须交纳销售费用,也就是说
申购价格=资产净值
可见,无论是计费式还是不计费的开放式基金,其申购价格都与其资产净值直接相关,成正比例关系。
2.赎回价格。
开放式基金承诺可以在任何时候根据投资者的个人意愿赎回其股票。对于赎回时不收取任何费用的开放式基金来说,
赎回价格=资产净值
有些开放式基金赎回时是收取费用的,费用的收取是按照基金投资年数不同而设立不同的赎回费率,持有基金券时间越长,费率越低,当然也有一些基金收取的是统一费率。在这种情况下,开放式基金的赎回价格与资产净值、附加费的关系是
赎回价格=资产净值+附加费
可见,开放式基金的价格仅与资产净值密切相关(在相关费用确定的条件下),只要资产净值估算准确,基金的申购和赎回没有任何问题。
七、封闭式基金的价格决定
封闭式基金的价格除受到上述因素影响以外,还受到杠杆效 应高低程度的影响。封闭式基金发行普通股是一次性的,即:基 金的资金额筹集完后就封闭起来,不再发行普通股。但是由于管理上的需要,这类公司亦可以通过发行优先股和公司债券,作为资本结构的一部分,形成末偿优先债券,并且能获得银行贷款。这对公司的普通股的股东来说,他们的收益就要受到杠杆作用的影响。优先证券对资产和收益有固定的权利。因此,当公司资产和收益总值(利息和优先股股息支付的收益)上升时,普通股的股东收益就会增加,他不仅可以得到更多的股息,而且还能获得资本收益。也就是说,当基金资产价值提高时,基金普通股增长更快;反之,当基金资产价值下降时,基金普通股也下降更快。这种杠杆效应往往使某些封闭式基金公司的普通股市场价值的增减超过总体市场的升降。封闭式基金由于不承担购回其股票的义务,其股票只有在公开市场上出售才能回收,以及有时由于杠杆效应的影响,使得封闭式基金的普通股价格不如开放式基金的普通股价格稳定,它们的价格就如同一个商业性公司的股票价格一样,其单股资产价值与市场价值之间存在着-个显著的离差。封闭式基金的价格决定可以利用普通股票的价格决定公式进行。
八、可转换证券
1.可转换证券的价值
可转换证券赋予投资者以将其持有的债务或优先股按规定的价格和比例,在规定的时间内转换成普通股的选择权。可转换证券有两种价值:理论价值和转换价值。
(1)理论价值。可转换证券的理论价值是指当它作为不具有转换选择权的一种证券的价值。估计可转换证券的理论价值,必须首先估计与它具有同等资信和类似投资特点的不可转换证券的必要收益率,然后利用这个必要收益算出它未来现金流量的现值。我们可以参考本章第一节中有关债券估价部分。
(2)转换价值。如果一种可转换证券可以立即转让,它可转换的普通股票的市场价值与转换比率的乘积便是转换价值,即
转换价值=普通股票市场价值×转换比率
式中:转换比率为债权持有人获得的每一份债券可转换的股票数。
2.可转换证券的市场价格。
可转换债券的市场价格必须保持在它的理论价值和转换价值之上。如果价格在理论价值之下,该证券价格低估,这是显然易见的;如果可转换证券价格在转换价值之下,购买该证券并立即转化为股票就有利可图,从而使该证券价格上涨直到转换价值之上。为了更好地理解这一点,我们引入转换平价这个概念。
(1)转换平价。转换平价是可转换证券持有人在转换期限内可以依据把债券转换成公司普通股票的每股价格,除非发生特定情形如发售新股、配股、送股、派息、股份的折细与合并,以及公司兼并、收购等情况下,转换价格一般不作任何调整。前文所说的转换比率,实质上就是转换价格的另一种表示方式。
转换平价=可转换证券的市场价格/转换比率
转换平价是一个非常有用的数字,因为一旦实际股票市场价格上升到转换平价水平,任何进一步的股票价格上升肯定会使可转换证券的价值增加。因此,转换平价可视为一个盈亏平衡点。
(2)转换升水和转换贴水。一般来说,投资者在购买可转换证券时都要支付一笔转换升水。每股的转换升水等于转换平价与普通股票当期市场价格(也称为基准股价)的差额,或说是可转换证券持有人在将债券转换成股票时,相对于当初认购转换证券时的股票价格(即基准胜股价)而作出的让步,通常被表示为当期市场价格的百分比,公式为
转换升水=转换平价一基准股价
九、优先认股权的价格
优先认股权是指在发行新股票时,应给予现有股东优先购买新股票的权利。其做法是给每个股东一份证书,写明他有权购买新股票的数量,数量多少根据股东现有股数乘以规定比例求得。一般来说,新股票的定价低于股票市价,从而使优先认股权具有价值。股东可以行使该权利,也可以转让他人。
1.附权优先认股权的价值。
优先认股权通常在某一股权登记日前颁发。在此之前购买的股东享有优先认股权,或说此时的股票的市场价格含有分享新发行股票的优先权,因此称为“附权优先认股权”,其价值可由下式求得。
M-(RN+S)=R (1)
式中:M为附权股票的市价;R为附权优先认股权的价值;N为购买1股股票所需的股权数;S为新股票的认购价。
该式可作以下解释:投资者在股权登记日前购买1股股票,应该付出市价M,同时也获得1股权;投资者也可购买申购l股新股所需的若干股权,价格为及RN,并且付出每股认购价S的金额。这两种选择都可获得1股股票,唯一差别在于,前一种选择多获得l股权。因此,这两种选择的成本差额,即M-(RN+S),必然等于股权价值R。
重写方程,可得
R=(M-S)/(N+1) (2)
[例2.14]如果分配给现有股东的新发行股票与原有股票的比例为1:5,每股认购价格为30元,原有股票每股市价为40元,则在股权登记日前此附权优先认股权的价值为
40-30/5+1=1.674元
于是,无优先认股权的股票价格将下降到
40-1.67=38.33(元)
2.除权优先认股权的价值。
在股权登记日以后,股票的市场价格中将不再含有新发行股票的认购权,其优先认股权的价值也按比例下降,此时就被称为“除权优先认股权”。其价值可由下式得到。
M-(RN+S)=0 (3)
式中:M为除权股票的市价;R为附权优先认股权的价值;N为购买1股股票所需的认股权数;S看为新股票的认购价。
此式原理与公式(1)完全一致。投资者可在公开市场购买1股股票,付出成本M,或者,他可购买申购1股股票所需的认股权,并付出l股的认购金额,其总成本为RN+S。这两种选择完全相同,都是为投资者提供l股股票,因此成本应是相同的,其差额为0。
把公式(3)进行改写,可得
R=(M-S)/N (4)
在前面例子中,除权后,队股权的价值应为
(38.33-30)/5=1.666(元)
3.优先认股权的杠杆作用。
优先认股权的主要特点之一就是它能提供较大程度的杠杆作用,就是说优先认股权的价格要比其可购买的股票的价格的增长或减小的速度快得多。比如说,某公司股票在除权之后价格为15元,其优先认股权的认购价格为5元,认购比率为1;4,则其优先认股权的价格为(15?元)/4=2.5元。假定公司收益改善的良好前景使股票价格上升到30元,增长100%,则优先认股权的价格为(;25?)/4=6.25元,增长(6.25?.6.25+5)/2.5=150%,远快于股票价格的增长速度
 爱华网
爱华网