DSP芯片的定点运算 dsp定点运算

发布时间：2018年04月10日 22:57:57分享人:没你也安好来源:互联网6
第3章 DSP芯片的定点运算

3.1 数 的 定 标
在定点DSP芯片中，采用定点数进行数值运算，其操作数一般采用整型数来表示。一个整
型数的最大表示范围取决于DSP芯片所给定的字长，一般为16位或24位。显然，字长越长
，所能表示的数的范围越大，精度也越高。如无特别说明，本书均以16位字长为例。
DSP芯片的数以2的补码形式表示。每个16位数用一个符号位来表示数的正负，0表示数值
为正，1则表示数值为负。其余15位表示数值的大小。因此
二进制数0010000000000011b＝8195
二进制数1111111111111100b＝-4
对DSP芯片而言，参与数值运算的数就是16位的整型数。但在许多情况下，数学运算过程
中的数不一定都是整数。那么，DSP芯片是如何处理小数的呢？应该说，DSP芯片本身无
能为力。那么是不是说DSP芯片就不能处理各种小数呢？当然不是。这其中的关键就是由
程序员来确定一个数的小数点处于16位中的哪一位。这就是数的定标。
通过设定小数点在16位数中的不同位置，就可以表示不同大小和不同精度的小数了。数
的定标有Q表示法和S表示法两种。表3.1列出了一个16位数的16种Q表示、S表示及它们所
能表示的十进制数值范围。
从表3.1可以看出，同样一个16位数，若小数点设定的位置不同，它所表示的数也就不同
。例如：
16进制数2000H＝8192，用Q0表示
16进制数2000H＝0.25，用Q15表示
但对于DSP芯片来说，处理方法是完全相同的。
从表3.1还可以看出，不同的Q所表示的数不仅范围不同，而且精度也不相同。Q越大，数
值范围越小，但精度越高；相反，Q越小，数值范围越大，但精度就越低。例如，Q0的数
值范围是-32768到+32767，其精度为1，而Q15的数值范围为-1到0.9999695，精度为
1/32768 =
0.00003051。因此，对定点数而言，数值范围与精度是一对矛盾，一个变量要
想能够表示比较大的数值范围，必须以牺牲精度为代价；而想提高精度，则数的表示范
围就相应地减小。在实际的定点算法中，为了达到最佳的性能，必须充分考虑到这一点
。
浮点数与定点数的转换关系可表示为：
浮点数(x)转换为定点数( )：
定点数( )转换为浮点数(x)：
例如，浮点数 x=0.5，定标 Q＝15，则定点数 ＝ ，式中
表示下取整。反之，一个用
Q＝15 表示的定点数16384，其浮点数为16384×2-15
＝16384/32768=0.5。
表3.1 Q表示、S表示及数值范围
Q表示S表示 十进制数表示范围
Q15 S0.15 -1≤X≤0.9999695
Q14 S1.14 -2≤X≤1.9999390
Q13 S2.13 -4≤X≤3.9998779
Q12 S3.12 -8≤X≤7.9997559
Q11 S4.11-16≤X≤15.9995117
Q10 S5.10-32≤X≤31.9990234
Q9S6.9-64≤X≤63.9980469
Q8S7.8-128≤X≤127.9960938
Q7S8.7-256≤X≤255.9921875
Q6S9.6-512≤X≤511.9804375
Q5 S10.5-1024≤X≤1023.96875
Q4 S11.4-2048≤X≤2047.9375
Q3 S12.3-4096≤X≤4095.875
Q2 S13.2-8192≤X≤8191.75
Q1 S14.1-16384≤X≤16383.5
Q0 S15.0-32768≤X≤32767

3.2 高级语言：从浮点到定点
在编写DSP模拟算法时，为了方便，一般都是采用高级语言(如C语言)来编写模拟程序
例3.1 256点汉明窗计算
int i;
float pi=3.14159;
float hamwindow[256];
for(i=0;i<256;i++)hamwindow[i]=0.54-0.46*cos(2.0*pi*i/255);
如果要将上述程序用某种定点DSP芯片来实现，则需将上述程序改写为DSP芯片的汇编语
言程序。为了DSP程序调试的方便及模拟定点DSP实现时的算法性能，在编写DSP汇编程序
之前一般需将高级语言浮点算法改写为高级语言定点算法。下面讨论基本算术运算的定
点实现方法。

3.2.1 加法/减法运算的C语言定点模拟
设浮点加法运算的表达式为：
float x,y,z;
z=x+y;
将浮点加法/减法转化为定点加法/减法时最重要的一点就是必须保证两个操作数的定标
值一样。若两者不一样，则在做加法/减法运算前先进行小数点的调整。为保证运算精度
，需使Q值小的数调整为与另一个数的Q值一样大。此外，在做加法/减法运算时，必须注
意结果可能会超过16位表示。如果加法/减法的结果超出16位的表示范围，则必须保留3
2位结果，以保证运算的精度。
1．结果不超过16位表示范围
设x的Q值为Qx，y的Q值为Qy，且Qx>Qy，加法/减法结果z的定标值为Qz，则
z＝x+y T
=
= T
所以定点加法可以描述为：
int x,y,z;
long temp;
temp＝y<<(Qx－Qy);
temp＝x＋temp;
z＝(int)(temp>>(Qx－Qz)), 若Qx≥Qz
z＝(int)(temp<<(Qz－Qx)), 若QxQ≤z
例3.2 定点加法
设x＝0.5，y＝3.1，则浮点运算结果为z＝x+y＝0.5+3.1＝3.6;
Qx＝15，Qy＝13，Qz＝13，则定点加法为：
x＝16384；y＝25395;
temp＝25395<<2＝101580;
temp＝x+temp＝16384+101580＝117964;
z＝(int)(117964L>>2)＝29491;
因为z的Q值为13，所以定点值z＝29491即为浮点值z＝29491/8192＝3.6。
例3.3 定点减法
设x＝3.0，y＝3.1，则浮点运算结果为z＝x-y＝3.0-3.1＝-0.1;
Qx＝13，Qy＝13，Qz＝15，则定点减法为：
x＝24576；y＝25295；
temp＝25395;
temp＝x-temp＝24576-25395＝-819;
因为Qx<Qz，故
z＝(int)(-819<<2)＝-3276。由于z的Q值为15，所以定点值z＝-3276即
为浮点值z＝-3276/32768"-0.1。
2．结果超过16位表示范围
设x的Q值为Qx，y的Q值为Qy，且Qx>Qy，加法结果z的定标值为Qz,则定点加法为：
int x，y；
long temp，z；
temp＝y<<(Qx-Qy)；
temp＝x＋temp;
z＝temp>>(Qx-Qz)，若Qx≥Qz
z＝temp<<(Qz-Qx)，若Qx≤Qz
例3.4 结果超过16位的定点加法
设x＝15000，y＝20000，则浮点运算值为z＝x＋y＝35000，显然z>32767，因此
Qx＝1，Qy＝0，Qz＝0，则定点加法为：
x＝30000；y＝20000；
temp＝20000<<1＝40000;
temp＝temp+x＝40000+30000＝70000;
z＝70000L>>1＝35000;
因为z的Q值为0，所以定点值z=35000就是浮点值，这里z是一个长整型数。
当加法或加法的结果超过16位表示范围时，如果程序员事先能够了解到这种情况，并且
需要保证运算精度时，则必须保持32位结果。如果程序中是按照16位数进行运算的，则
超过16位实际上就是出现了溢出。如果不采取适当的措施，则数据溢出会导致运算精度
的严重恶化。一般的定点DSP芯片都设有溢出保护功能，当溢出保护功能有效时，一旦出
现溢出，则累加器ACC的结果为最大的饱和值(上溢为7FFFH，下溢为8001H)，从而达到防
止溢出引起精度严重恶化的目的。

3.2.2 乘法运算的C语言定点模拟
设浮点乘法运算的表达式为：
float x,y,z;
z = xy;
假设经过统计后x的定标值为Qx，y的定标值为Qy，乘积z的定标值为Qz，则
z = xy T
= T
=
所以定点表示的乘法为：
int x,y,z;
long temp;
temp = (long)x;
z = (temp×y) >> (Qx+Qy-Qz);
例3.5 定点乘法
设x = 18.4，y = 36.8，则浮点运算值为z =18.4×36.8 = 677.12;
根据上节，得Qx = 10，Qy = 9，Qz = 5，所以
x = 18841；y = 18841；
temp = 18841L;
z = (18841L*18841)>>(10+9-5) =354983281L>>14 = 21666;
因为z的定标值为5，故定点 z = 21666即为浮点的 z = 21666/32 = 677.08。
3.2.3 除法运算的C语言定点模拟
设浮点除法运算的表达式为：
float x,y,z;
z = x/y;
假设经过统计后被除数x的定标值为Qx，除数y的定标值为Qy，商z的定标值为Qz，则
z = x/y T
= T
所以定点表示的除法为：
int x,y,z;
long temp;
temp = (long)x;
z = (temp<<(Qz-Qx+Qy))/y;
例3.6 定点除法
设x = 18.4，y = 36.8，浮点运算值为z = x/y = 18.4/36.8 = 0.5;
根据上节，得Qx = 10，Qy = 9，Qz = 15；所以有
x = 18841, y = 18841;
temp = (long)18841;
z = (18841L<<(15-10+9))/18841 =308690944L/18841 = 16384;
因为商z的定标值为15，所以定点z = 16384即为浮点 z = 16384/215= 0.5。

3.2.4 程序变量的Q值确定
在前面几节介绍的例子中，由于x、y、z的值都是已知的，因此从浮点变为定点时Q值很
好确定。在实际的DSP应用中，程序中参与运算的都是变量，那么如何确定浮点程序中变
量的Q值呢？
从前面的分析可以知道，确定变量的Q值实际上就是确定变量的动态范围，动态范围确定
了，则Q值也就确定了。
设变量的绝对值的最大值为 ，注意 必须小于或等于32767。取一个整数n，使它满足
则有Q = 15-n
例如，某变量的值在-1至＋1之间，即 <1，因此n = 0，Q＝15-n = 15。
确定了变量的 就可以确定其Q值，那么变量的
又是如何确定的呢？一般来说，确定变量
的 有两种方法：一种是理论分析法，另一种是统计分析法。
1．理论分析法
有些变量的动态范围通过理论分析是可以确定的。例如：
(1) 三角函数，y = sin(x)或y = cos(x)，由三角函数知识可知，|y|≤1；
(2) 汉明窗，y(n) = 0.54-0.46cos [2pn/(N-1)] ，0≤n≤N-1。因为-1≤cos
[2pn/(N
-1)]≤1，所以0.08≤y(n)≤1.0；
(3) FIR卷积。y(n)= ，设 ，且x(n)是模拟信号12位量化值，即有≤211，则
≤211；

(4) 理论已经证明，在自相关线性预测编码(LPC)的程序设计中，反射系数
满足下列不
等式：
，i= 1,2,…,p, p为LPC的阶数。
2．统计分析法
对于理论上无法确定范围的变量，一般采用统计分析的方法来确定其动态范围。所谓统
计分析，就是用足够多的输入信号样值来确定程序中变量的动态范围，这里输入信号一
方面要有一定的数量，另一方面必须尽可能地涉及各种情况。例如，在语音信号分析中
，统计分析时就必须采集足够多的语音信号样值，并且在所采集的语音样值中，应尽可
能地包含各种情况，如音量的大小、声音的种类(男声、女声)
等。只有这样，统计出来的结果才能具有典型性。
当然，统计分析毕竟不可能涉及所有可能发生的情况，因此，对统计得出的结果在程序
设计时可采取一些保护措施，如适当牺牲一些精度，Q值取比统计值稍大些，使用DSP芯
片提供的溢出保护功能等。

3.2.5 浮点至定点变换的C程序举例
本节通过一个例子来说明C程序从浮点变换至定点的方法。这是一个对语音信号(0.3kHz
~3.4kHz)进行低通滤波的C语言程序，低通滤波的截止频率为800Hz，滤波器采用19点的
有限冲击响应FIR滤波。语音信号的采样频率为8kHz，每个语音样值按16位整型数存放在
insp.dat文件中。
例3.7 语音信号800Hz 19点FIR低通滤波C语言浮点程序
＃i nclude <stdio.h>
const int length = 180
void filter(int xin[ ],int xout[ ],int n,float h[]);

static float h[19]=
{0.01218354,-0.009012882,-0.02881839,-0.04743239,-0.04584568,
-0.008692503,0.06446265,0.1544655,0.2289794,0.257883,
0.2289794,0.1544655,0.06446265,-0.008692503,-0.04584568,
-0.04743239,-0.02881839,-0.009012882,0.01218354};
static int x1[length+20];

void filter(int xin[ ],int xout[ ],int n,float h[])
{
int i,j;
float sum;
for(i=0;i<length;i++) x1[n+i-1]=xin[i];
for (i=0;i<length;i++)
{
sum=0.0;
for(j=0;j<n;j++) sum+=h[j]*x1[i-j+n-1];
xout[i]=(int)sum;
}
for(i=0;i<(n-1);i++)x1[n-i-2]=xin[length-1-i];
}

void main( )
{
FILE*fp1,*fp2;
intframe,indata[length],outdata[length];
fp1=fopen(insp.dat,"rb");
fp2=fopen(outsp.dat,"wb");
frame=0;
while(feof(fp1)==0)
{
frame++;
printf("frame=%dn",frame);
for(i=0;i<length;i++)indata[i]=getw(fp1);
filter(indata,outdata,19,h);
for(i=0;i<length;i++)putw(outdata[i],fp2);
}
fcloseall();
return(0);
}
例3.8 语音信号800Hz 19点FIR低通滤波C语言定点程序
＃i nclude <stdio.h>
const int length=180;
void filter(int xin[ ],int xout[ ],int n,int h[]);
static inth[19]={399,-296,-945,-1555,-1503,-285,2112,5061,7503,8450,
7503,5061,2112,-285,-1503,-1555,-945,-296,399};
static int x1[length+20];

void filter(int xin[ ],int xout[ ],int n,int h[])
{
int i,j;
long sum;
for(i=0;i<length;i++) x1[n+i-1]=xin[i];
for (i=0;i<length;i++)
{
sum=0;
for(j=0;j<n;j++)sum+=(long)h[j]*x1[i-j+n-1];
xout[i]=sum>>15;
}
for(i=0;i<(n-1);i++)x1[n-i-2]=xin[length-i-1];
}
主程序与浮点的完全一样。

3.3 DSP定点算术运算
定点DSP芯片的数值表示是基于2的补码表示形式。每个16位数用1个符号位、i个整数位
和15-i个小数位来表示。因此数00000010.10100000表示的值为
=2.625，这个数可用Q8
格式(８个小数位)来表示，它表示的数值范围为-128~+127.996，一个Q8定点数的小数精
度为1/256=0.004。
虽然特殊情况(如动态范围和精度要求)必须使用混合表示法，但是，更通常的是全部以
Q15格式表示的小数或以Q0格式表示的整数来工作。这一点对于主要是乘法和累加的信号
处理算法特别现实，小数乘以小数得小数，整数乘以整数得整数。当然，乘积累加时可
能会出现溢出现象，在这种情况下，程序员应当了解数学里面的物理过程以注意可能的
溢出情况。下面讨论乘法、加法和除法的DSP定点运算，汇编程序以TMS320C25为例。

3.3.1 定点乘法
2个定点数相乘时可以分为下列3种情况：
1．小数乘小数
Q15×Q15＝Q30
例3.9 0.5*0.5 = 0.25
0.100000000000000 ；Q15
×0.100000000000000；Q15
00.010000000000000000000000000000=0.25；Q30
2个Q15的小数相乘后得到1个Q30的小数，即有2个符号位。一般情况下相乘后得到的满
度数不必全部保留，而只需保留16位单精度数。由于相乘后得到的高16位不满15位的小
数精度，为了达到15位精度，可将乘积左移1位，下面是上述乘法的TMS320C25程序:
LT OP1 ；OP1=4000H(0.5/Q15)
MPYOP2；OP2=4000H(0.5/Q15)
PAC
SACHANS,1；ANS=2000H(0.25/Q15)
2．整数乘整数
Q0×Q0 = Q0
例3.10 17×(-5)=-85
0000000000010001=17
×1111111111111011=-5
11111111111111111111111110101011=-85
3．混合表示法
许多情况下，运算过程中为了既满足数值的动态范围又保证一定的精度，就必须采用Q0
与Q15之间的表示法。比如，数值1.2345，显然Q15无法表示，而若用Q0表示，则最接近
的数是1，精度无法保证。因此，数1.2345最佳的表示法是Q14。
例3.11 1.5×0.75 = 1.125
01.10000000000000 =1.5；Q14
× 00.11000000000000 =0.75；Q14
0001.0010000000000000000000000000 = 1.125;Q28
Q14的最大值不大于2，因此，2个Q14数相乘得到的乘积不大于4。
一般的，若一个数的整数位为 i位，小数位为 j 位，另一个数的整数位为 m
位，小数位为 n 位，则这两个数的乘积为 ( i + m )位整数位和(j +
n)位小数位。这个乘积的
最高16位可能的精度为( i + m )整数位和(15 - i - m)小数位。
但是，若事先了解数的动态范围，就可以增加数的精度。例如，程序员了解到上述乘积
不会大于1.8，就可以用Q14数表示乘积，而不是理论上的最佳情况Q13。例3.11的TMS32
0C25程序如下：
LT OP1 ;OP1 =6000H(1.5/Q14)
MPY OP2 ;OP2 = 3000H(0.75/Q14)
PAC
SACHANS,1;ANS＝2400H(1.125/Q13)
上述方法为了保证精度均对乘的结果舍位，结果所产生的误差相当于减去1个LSB(最低位
)。采用下面简单的舍入方法，可使误差减少二分之一。
LT OP1
MPY OP2
PAC
ADD ONE，14 (上舍入)
SACHANS，1
上述程序说明，不管ANS为正或负，所产生的误差是1/2
LSB，其中存储单元ONE的值为1。

3.3.2 定点加法
乘的过程中，程序员可不考虑溢出而只需调整运算中的小数点。而加法则是一个更加复
杂的过程。首先，加法运算必须用相同的Q点表示；其次，程序员或者允许其结果有足够
的高位以适应位的增长，或者必须准备解决溢出问题。如果操作数仅为16位长，其结果
可用双精度数表示。下面举例说明16位数相加的两种途径。
1．保留32位结果
LAC OP1 ;(Q15)
ADD OP2 ;(Q15)
SACHANSHI ;(高16位结果)
SACLANSLO ;(低16位结果)
2．调整小数点保留16位结果
LAC OP1,15 ;(Q14数用ACCH表示)
ADD OP2,15 ;(Q14数用ACCH表示)
SACH ANS;(Q14)
加法运算最可能出现的问题是运算结果溢出。TMS320提供了检查溢出的专用指令BV，此
外，使用溢出保护功能可使累加结果溢出时累加器饱和为最大的整数或负数。当然，即
使如此，运算精度还是大大降低。因此，最好的方法是完全理解基本的物理过程并注意
选择数的表达方式。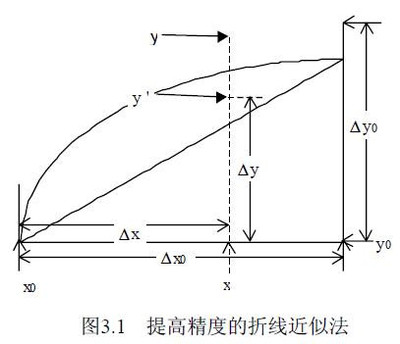
DSP芯片的定点运算 dsp定点运算

3.3.3 定点除法
在通用DSP芯片中，一般不提供单周期的除法指令，为此必须采用除法子程序来实现。二
进制除法是乘法的逆运算。乘法包括一系列的移位和加法，而除法可分解为一系列的减
法和移位。下面来说明除法的实现过程。
设累加器为8位，且除法运算为10除以3。除的过程就是除数逐步移位并与被除数比较的
过程，在每一步进行减法运算，如果能减则将位插入商中。
(1) 除数的最低有效位对齐被除数的最高有效位。
00001010
－00011000
11110010
(2) 由于减法结果为负，放弃减法结果，将被除数左移一位再减。
00010100
－00011000
11111000
(3) 结果仍为负，放弃减法结果，被除数左移一位再减。
00101000
－00011000
00010000
(4) 结果为正，将减法结果左移一位后加１，作最后一次减。
00100001
－00011000
00001001
(5) 结果为正，将结果左移一位加1得最后结果。高４位代表余数，低4位表示商。
00010011
即商为0011=3，余数为0001=1。
TMS320没有专门的除法指令，但使用条件减指令SUBC可以完成有效灵活的除法功能。使
用这一指令的唯一限制是两个操作数必须为正。程序员必须事先了解其可能的运算数的
特性，如其商是否可以用小数表示及商的精度是否可被计算出来。这里每一种考虑可影
响如何使用SUBC指令的问题。下面给出两种不同情况下的TMS320C25除法程序。
(1) 分子小于分母
DIV_A:
LTNUMERA
MPYDENOM
PAC
SACHTEMSGN;取商的符号
LACDENOM
ABS
SACLDENOM;使分母为正
ZALHNUMERA;使分子为正
ABS
RPTK 14
SUBCDENOM;除循环15次
SACLQUOT
LACTEMSGN
BGEZA1;若符号为正,则完成
ZAC
SUBQUOT
SACLQUOT;若为负,则商为负
A1: RET
这个程序中，分子在NUMERA中，分母在DENOM中，商存在QUOT中，TEMSGN为暂存单元。
(2) 规定商的精度
DIV_B:
LTNUMERA
MPYDENOM
PAC
SACHTEMSGN;取商的符号
LACDENOM
ABS
SACLDENOM;使分母为正
LACK 15
ADDFRAC
SACLFRAC;计算循环计数器
LACNUMERA
ABS;使分子为正
RPTFRAC
SUBCDENOM;除循环16+FRAC次
SACLQUOT
LACTEMSGN
BGEZB1;若符号为正,则完成
ZAC
SUBQUOT
SACLQUOT;若为负,则商为负
B1: RET
与DIV_A相同，这个程序中，分子在NUMERA中，分母在DENOM中，商存在QUOT中，TEMSGN
为暂存单元。FRAC中规定商的精度，如商的精度为Q13，则调用程序前FRAC单元中的值应
为13。

3.4 非线性运算的定点快速实现
在数值运算中，除基本的加减乘除运算外，还有其他许多非线性运算，如对数运算、开
方运算、指数运算、三角函数运算等，实现这些非线性运算的方法一般有：(1)调用DSP
编译系统的库函数；(2)查表法；(3)混合法。下面分别介绍这三种方法。
1．调用DSP编译系统的库函数
TMS320C2X/C5X
的C编译器提供了比较丰富的运行支持库函数。在这些库函数中，包含了
诸如对数、开方、三角函数、指数等常用的非线性函数。在C程序中(也可在汇编程序中
)只要采用与库函数相同的变量定义，就可以直接调用。例如，在库函数中，定义了以1
0为底的常用对数log10( )：
＃include <math.h>
double log10(double x);
在C程序中按如下方式调用：
float x,y;
x = 10.0;
y = log10(x);
从上例可以看出，库函数中的常用对数log10(
)要求的输入值为浮点数，返回值也为浮
点数，运算的精度完全可以保证。直接调用库函数非常方便，但由于运算量大，很难在
实时DSP中得到应用。
2．查表法
在实时DSP应用中实现非线性运算，一般都采取适当降低运算精度来提高程序的运算速度
。查表法是快速实现非线性运算最常用的方法。采用这种方法必须根据自变量的范围和
精度要求制作一张表格。显然输入的范围越大，精度要求越高，则所需的表格就越大，
即存储量也越大。查表法求值所需的计算就是根据输入值确定表的地址，根据地址就可
得到相应的值，因而运算量较小。查表法比较适合于非线性函数是周期函数或已知非线
性函数输入值范围这两种情况，例3.12和例3.13分别说明这两种情况。
例3.12 已知正弦函数y=cos(x)，制作一个512点表格，并说明查表方法。
由于正弦函数是周期函数，函数值在－1至＋1之间，用查表法比较合适。
由于Q15的表示范围为－1至32767/32768之间，原则上讲－1至＋1的范围必须用Q14表示
。但一般从方便和总体精度考虑，类似情况仍用Q15表示，此时＋1用32767来表示。
(1) 产生512点值的C语言程序如下所示:
#define N 512
#define pi 3.14159
int sin_tab[512];
void main( )
{
int i;
for(i=0;i<N;i++)sin_tab[i]=(int)(32767*sin(2*pi*i/N));
}
(2) 查表
查表实际上就是根据输入值确定表的地址。设输入x在0~2p之间，则x对应于512点表的

址为：index = (int)(512*x/2p)，则 y = sin(x) = sin_tab[index]。
如果x用Q12定点数表示，将512/2p用Q8表示为
20861，则计算正弦表的地址的公式为：
index = (x*20861L)>>20。
例3.13
用查表法求以2为底的对数，已知自变量取值范围为0.5~1,要求将自变量范围均
匀划分为10等分。试制作这个表格并说明查表方法。
(1) 做表：
y = log2(x)，由于x在0.5到1之间，因此y在-1到0之间，x和y均可用Q15表示。由于对x
均匀划分为10段，因此，10段对应于输入x的范围如表3.2所示。若每一段的对数值都取
第1点的对数值，则表中第1段的对数值为y0(Q15) =
(int)(log2(0.5)×32768)，第2段
的对数值为y1(Q15) = (int)(log2(0.55)×32768)，依次类推。
表3.2 logtab0 10点对数表(输入0.5~1)
地址输入值 对数值(Q15)
00.50~0.55 -32768
10.55~0.60 -28262
20.60~0.65 -24149
30.65~0.70 -20365
40.70~0.75 -16862
50.75~0.80 -13600
60.80~0.85 -10549
70.85~0.90 -7683
80.90~0.95 -4981
90.95~1.00 -2425
(2) 查表:
查表时，先根据输入值计算表的地址，计算方法为：index=((x-16384)×20)>>15。式中
，index就是查表用的地址。例如，已知输入x= 26869，则index=6，因此y=-10549。
3．混合法
(1) 提高查表法的精度
上述方法查表所得结果的精度随表的大小而变化，表越大，则精度越高，但存储量也越
大。当系统的存储量有限而精度要求也较高时，查表法就不太适合。那么能否在适当增
加运算量的情况下提高非线性运算的精度呢？下面介绍一种查表结合少量运算来计算非
线性函数的混合法，这种方法适用于在输入变量的范围内函数呈单调变化的情形。
混合法是在查表的基础上采用计算的方法以提高当输入值处于表格两点之间时的精度。
提高精度的一个简便方法是采用折线近似法，如图3.1所示。
仍以求以2为底的对数为例(例3.13)。设输入值为x，则精确的对数值为y，在表格值的两
点之间作一直线，用y＇作为y的近似值，则有：
y＇＝y0＋ y其中y0由查表求得。现在只需在查表求得y0的基础上增加 y即可。
y的计算方法如下：
y=( x/ x0) y= x( y0/ x0)
式中 y0/ x0对每一段来说是一个恒定值，可作一个表格直接查得。此外计算
x时需用到
每段横坐标的起始值，这个值也可作一个表格。这样共有三个大小均为10的表格，分别
为存储每段起点对数值的表logtab0、存储每段 y0/ x0
值的表logtab1和存储每段输入
起始值x0的表logtab2，表logtab1和表logtab2可用下列两个数组表示：
intlogtab1[10]={22529,20567,18920,17517,16308,
15255,14330,13511,12780,12124};
intlogtab2[10]={16384,18022,19660,21299,22938,
24576,26214,27853,29491,31130};
综上所述，采用混合法计算对数值的方法可归纳为：
①根据输入值，计算查表地址：index=((x-16384)×20)>>15;
②查表得y0=logtab0[index];
③计算 x=x-logtab2[index];
④计算 y＝( x×logtab1[index])>>13;
⑤计算得结果y=y0+ y。
例3.14 已知x=0.54，求log2(x)。
0.54的精确对数值为y=log2(0.54)=-0.889。
混合法求对数值的过程为：
①定标Q15，定标值x=0.54*32768=17694；
②表地址index=((x-16384)×20)>>15=0;
③查表得y0=logtab0[0]=-32768;
④计算 x=x-logtab2[0]=17694-16384=1310;
⑤计算 y＝(xlogtab1[0])>>13=(1310*22529L)>>13=3602;
⑥计算结果y=y0+ y=-32768+3602=-29166。
结果y为Q15定标，折算成浮点数为-29166/32768=-0.89，可见精度较高。
(2) 扩大自变量范围
如上所述，查表法比较适用于周期函数或自变量的动态范围不是太大的情形。对于像对
数这样的非线性函数，输入值和函数值的变化范围都很大。如果输入值的变化范围很大
，则作表就比较困难。那么能否比较好地解决这个问题，既不使表格太大，又能得到比
较高的精度呢？下面讨论一种切实可行的方法。
设x是一个大于0.5的数，则x可以表示为下列形式：
x =式中，0.5≤m≤1.0，e为整数。则求 x 的对数可以表示为：
log2(x) = log2( ) = log2(m) + log2( ) = e + log2(m)
也就是说，求x的对数实际上只要求
m的对数就可以了，而由于m的数值在0.5~1.0之间，
用上面介绍的方法是完全可以实现的。例如：
log2(10000) = log2(0.61035× ) = log2(0.61035) + 14 = 13.2877
可见，如果一个数可以用比较简便的方法表示为上面的形式，则求任意大小数的对数也
是比较方便的。TMS320C2X/C5X指令集提供了一条用于对ACC中的数进行规格化的指令
NORM ，该指令的作用就是使累加器中的数左移，直至数的最高位被移至累加器的第30位
。例如，对数值10000进行规格化的TMS320C25程序为：
LAC #10000
SACLTEMP
ZALHTEMP
LAR AR1,#0FH
RPT 14
NORM *－
上述程序执行后，AR1=#0eH，ACCH=2000(10进制)。对一个16位整数 x
进行上述程序处理实际上就是做这样一个等效变换：
x =
其中，寄存器AR1包含的值为15-Q，累加器ACC高16位包含的值为
，其数值在16384~32768之间。
例3.15 实现以2为底的对数的C定点模拟程序
intlogtab0[10]＝{-32768,-28262,-24149,-20365,-16862,
-13600,-10549,-7683,-4981,-2425};
intlogtab1[10]＝{22529,20567,18920,17517,16308,
15255,14330,13511,12780,12124};
intlogtab2[10]＝{16384,18022,19660,21299,22938,
24576,26214,27853,29491,31130};
intlog2_fast(int Am)
{
intpoint,point1;
intindex,x0,dx,dy,y;
point＝0;
while(Am<16384){point++；Am＝Am<<1;}
point1＝(15-point-4)*512;
index＝((Am-16384)*20L)>>15;
dx＝Am-logtab2[index];
dy＝((long)dx*logtab1[index])>>13;
y＝(dy+logtab0[index])>>6;
y＝point1+y;
return (y);
}
上述程序中，输入值Am采用Q4表示，输出采用Q9表示，如果输入输出的Q值与上面程序中
的不同，则应做相应的修改。

3.5小 结
本章讨论了DSP芯片进行定点运算所涉及的一些基本问题，这些问题包括：数的定标，D
SP程序的定点模拟，DSP芯片的定点运算以及定点实现非线性函数的快速实现方法等。充
分理解这些问题对于用定点芯片实现DSP算法具有非常重要的作用。

  
定点dsp和浮点dsp 

爱华网本文地址 » http://www.aihuau.com/a/25101013/187101.html

更多阅读

PHP的位运算 php 位运算 权限

位运算??? (http://club.21php.com/showthread.php?t=5386)zww232004年06月19日 10:32 AM位运算???<?phpecho "位运算符的例子！<br>";$a=5; //用二进制表示a=101;$b=2; //用二进制表示b=010;$c=$a&amp;$b

c中的移位运算 java中的移位运算

C++位运算,看高手都是运用的灵活自如,打算从今天开始学习他!收藏每次看到位运算的地方,都比较迷糊.以前学习C的时候也不求甚解,到现在看来,觉得位运算和指针在C++基本知识里是最难理解,最难融会贯通的东西.尤其是位运算,用好了可以"

声明:《DSP芯片的定点运算 dsp定点运算》为网友没你也安好分享！如侵犯到您的合法权益请联系我们删除