这个方法比高中教材中“用两点间的距离”公式求“两角和余弦”方法要妙。同时,它好象勾起了我高中时期的记忆,感觉我高中时期知道的就是这个方法。嗨,数学真美妙啊,此方法真是值得记忆。
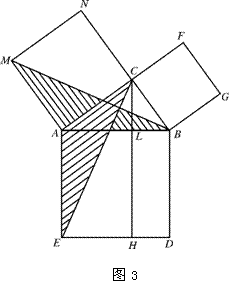
再说这个图,由于应用了“模块移动法”证明“勾股定理”,显得有趣易记。同时,还进一步揭示了(a+b)^2= a^2 + b^2 +2ab,美啊。
--------------------------------------------------------------------------
还有人用下面的方法,有时间可看,没时间就算了。
两角和的正弦公式我们是如何推导的?
两角和的正弦与余弦公式:
(1)sin(α+β)=sinαcosβ+cosαsinβ;
(2)cos(α+β)=cosαcosβ-sinαsinβ;
我们的思路是在直角坐标系的单位圆中,
直接用平面几何的知识来推导:
sin(α+β)=sinαcosβ+cosαsinβ;
再用诱导公式证明: cos(α+β)=cosαcosβ-sinαsinβ;
如图所示:∠AOC=α,∠BOA=β,∠BOC=β+α。
且BD⊥OA于D,DC⊥Ox于C,BF⊥Ox于F,DE⊥BF于E,
则∠ABE=α(一个角的两边与另一个角的两边互相垂直,则这两个角相等或互补)
∵ OA=OB=1、OD=OBcosβ、DC=ODsinα
∴EF=DC=sinαcosβ。
∵ OA=OB=1、BD=OBsinβ、BE=BDcosα
∴ BE=sinβcosα。
∵ BF=BE+EF;BF=OBsin(α+β)= sin(α+β);
∴ sin(α+β)=sinαcosβ+cosαsinβ;
∴cos(α+β)= sin(90°-α-β)
=sin[(90°-α)+(-β)]
=sin(90°-α)cos(-β)+ cos(90°-α)sin(-β)
=cosαcosβ-sinαsinβ;
该证法比高中教材证法简单的多!你觉得精彩吧!
 爱华网
爱华网