利用单位圆方法证明 sin(α+β)=… 与cos(α+β)=…,是进一步证明大部分三角函数公式的基础。
1、sin(α+β)=sinαcosβ+cosαsinβ
在笛卡尔坐标系中以原点O为圆心作单位圆,在单位圆中作以下线段:
如图中所示,容易看出:
sin(α+β)=CF;sinα=AB;cosα=OB;sinβ=CD;cosβ=OD
则:
----------------------------------------------------------------------------------------------
平面几何的证明方法:如图所示,过程见下面的【评论】中新浪网友的提示
(非常感谢这位网友的提示,让我们看到了证明一个定理的多种途径,真是妙不可言!)
----------------------------------------------------------------------------------
附:如何证明托勒密定理?
见 http://hyz0.blog.sohu.com/69610635.html
http://iask.sina.com.cn/b/2459822.html
托勒密(Ptolemy)定理指出,圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆内接四边形中,两对角线所包矩形的面积等于 一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.(具体的推导方法详见数学目录下的博文,来自网友的提供!)
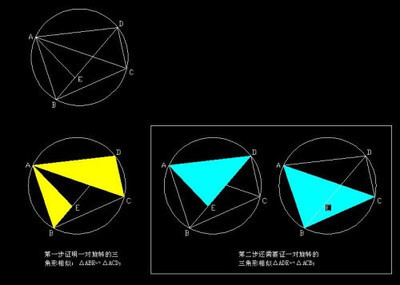
思路:托勒密定理在平面几何中赫赫有名,其难点在于:把一条对角线分割成两条线段DE和BE。第一步证明一对旋转的三角形相似:△ABE∽△ACD;第二步还需要证一对旋转的三角形相似△ADE∽△ACB;只有这两对相似的三角形出来了才能得到结论。
证明:以AB为边,作一个角等于已知角:即∠BAE=∠DAC;
在ΔABE和ΔACD中,
∵∠BAE=∠DAC;
∠ABE=∠ACD;
∴△ABE∽△ACD;
∴AB·DC=BE·AC①
∵∠BAE=∠DAC;
∴∠DAE=∠CAB;
在ΔADE和ΔACB中,
∵∠ADE=∠ACB;
∠DAE=∠CAB;
∴△ADE∽△ACB;
∴AD·BC=DE·AC②
∴ ①+②得:
AB·DC+ AD·BC= BE·AC+ DE·AC=(BE+DE)·AC=BD·AC。
结论:该命题对于圆内接的任意四边形都成立。最初是由数学家托勒密想出来的,叫做托勒密定理。“当你遇到AB·DC+AD·BC=AC·BD这样的等积式时,如果等式左边可以合二为一,则考虑证一对三角形相似,否则,在AC、BD的其中一条线段上找到一个分点,构造两个三角形相似。”
 爱华网
爱华网