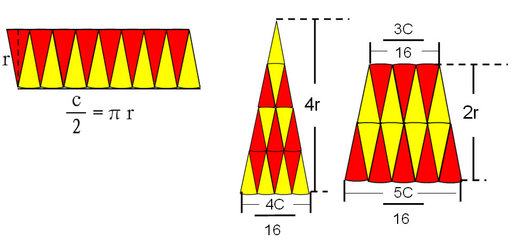
圆的周长课后练习题
一、填空。
(1)圆的周长总是直径的()多一些。
(2)圆的()除以()的商是一个固定的数,我们把它叫做( ),用字母()表示,计算时通常取()。
(3)如果用C来表示圆的周长,用d来表示圆的直径,那么圆的周长公式用字母可以表示为();如果用C来表示圆的周长,用r来表示圆的半径,那么圆的周长公式用字母可以表示为()。
(设计意图:基础练习及时检查学生所学的知识和技能,及时巩固运用所学的新知。)
二、填表,并说出你是如何计算的。

半径/cm | 直径/cm | 周长/cm |
3.5 | ||
12 | ||
9.42 |
(设计意图:通过练习,巩固新知,加深对新知识的理解,把所学知识进一步转化为能力,在练习中发展智力,培养优良的学习品质和学习习惯。)
三、根据已学的知识来解决生活中的问题。
1.把一根长18.84厘米的铁丝做成一个最大的圆(接头处忽略不计),这个圆的直径是多少厘米?半径是多少厘米?
2.如果一个铁环的半径是0.3米,20米长的铁丝最多能做多少个这样的铁环?
3.一个圆形水池,直径是10米,笑笑沿水池走了一圈,她大约走了多少米?
4.一只钟表的分针长10厘米,从1时到2时,分针的针尖走过了多少厘米?
5.一辆汽车轮胎的外直径是1.5米,它转动一周前进多少米?如果它每分钟转200周,它一分钟前进多少米?
6.一辆自行车的轮胎的外直径是0.7米,如果平均每分转90周,通过一座989.1长的桥,需要几分钟?
(设计意图:让学生对所学知识做到灵活运用,培养学生活学活用的本领。通过圆周长公式的应用,使得学生内化了公式,掌握了新知,同时数学知识也和学生的生活实际结合起来,使学生明白,我们所学的数学是身边的数学、是有趣的、有用的数学,让学生充分体会到数学来源于生活又运用于生活的思想。)
练习后的反思:
1.第一道练习题是圆的周长最基础的部分,学生通过学习新课,都能够轻松完成。
2.第二题,学生在练习中,已知半径求直径和周长,学生能够准确完成,并能说出解题思路;已知直径求半径和周长,学生也能够准确完成;问题是已知圆的周长求圆的直径和半径,这一道题部分同学完成时有一些困难,有的同学仅能求出直径,不会求半径,感觉学生只会纯粹的模仿,而不去动脑。
3.解决实际问题时,学生缺少生活经验,不知道自己每一步求的是什么?比如第5题,学生不明白车轮转动一周前进的路程就是求车轮的周长,所以在解决问题时不会解决,还有个别同学解题方法能够掌握,只是在计算时正确率较差,说明学生的计算能力有待提高。
4. 从整体的练习情况来看,表面上学生对于半径、直径、周长的计算公式背的头头是道,但是到了真正解决问题时,学生就不能应用自如,学生对于稍复杂的题目不能清晰地作出分析。例如自行车的外直径,每分钟转的周数与一分钟经过的路程之间的必然关系不能联系起来,他们想象不出其中的关联,另外其中的计算也是错误百出。
 爱华网
爱华网