小学奥数题0分
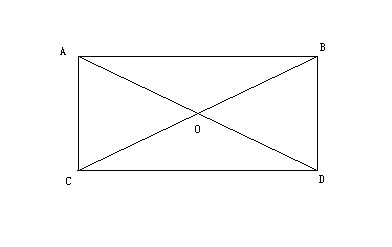
已知一个长方形的长是宽的2倍,对角线长10厘米,求长方形的面积.
如图:根据题意:2AB=AD,BD=10cm
由此可得:AE=2BE=1/2DE,即:4BE=DE,BE+DE=5BE=10cm
AE=2BE=4cm
长方形面积=2*(1/2)*AE*BD=2*(1/2)*4*10=40cm^2
(转自学而思网)六年级奥数几何知识 组合图形的面积
|
1、已知长方形ABCD的对角线BD长15厘米,长是宽的2倍,如图1,你能算出长方形ABCD的面积吗?
【分析】根据图形可以轻松解出来。
右对角线组成的正方形面积是小正方形面积的5倍(里面包括一个小正方形,两个长方形,而一个长方形面积是2倍的小正方形面积),小正方形面积是45,所以长方形面积是90平方厘米。
2.有一长方形,它的长与宽的比是5:2,对角线长29厘米,求这个长方形的面积.
3、有一个长方形,长是宽的5倍,对角线长52厘米,求这个长方形的面积. 训练指导5P135_14
答案:520.
用四个这样的长方形拼成如图所示的有空洞的正方形.正方形BDEF的边长为52,其中有26个小正方形,每个小正方形的面积是:
52*52/26=104, 104*5=520.
4、有一个长方形,长是宽的4倍,且对角线的长度是17厘米,求这个正方形的面积。
分析与解要求出长方形的面积,必须要知道它的长和宽,由题意可知(如图1),AB=4BC,AC=17厘米,仅靠这些条件,小学阶段是不能求出AB、BC的。
不妨按图2构造正方形。长方形ABCD是4×1个方格,把它扩充为5×5个方格的正方形,并且在它的内部作出以AC为边长的正方形ACGH,容易求出ACGH的面积为(17×17)平方厘米。又正方形ACGH内部有(3×3=)9个方格和4个三角形ABC,两个△ABC可以拼成4个方格,4个就可以拼成8个方格,因此正方形ACGH共由(9+8=)17个方格组成。每个方格的面积是(17×17÷17=)17平方厘米,而长方形ABCD是由4个方格组成的,所以它的面积是(17×4=)68平方厘米。
转载
构造正方形三例
江苏省无锡市金城小学 胡剑
有一些题目,我们可以通过构造正方形,来使题目变得更加简单、直观,从而能够准确、快捷地解答它。请看下面三例:
例1有一个长方形,长是宽的4倍,且对角线的长度是17厘米,求这个正方形的面积。
分析与解要求出长方形的面积,必须要知道它的长和宽,由题意可知(如图1),AB=4BC,AC=17厘米,仅靠这些条件,小学阶段是不能求出AB、BC的。
不妨按图2构造正方形。长方形ABCD是4×1个方格,把它扩充为5×5个方格的正方形,并且在它的内部作出以AC为边长的正方形ACGH,容易求出ACGH的面积为(17×17)平方厘米。又正方形ACGH内部有(3×3=)9个方格和4个三角形ABC,两个△ABC可以拼成4个方格,4个就可以拼成8个方格,因此正方形ACGH共由(9+8=)17个方格组成。每个方格的面积是(17×17÷17=)17平方厘米,而长方形ABCD是由4个方格组成的,所以它的面积是(17×4=)68平方厘米。
例2在一个等腰直角三角形中,最长的一条边是12厘米,这个三角形的面积是多少?
分析与解依题意作示意图(见图3),可知AB=AC,且BC=12厘米。
我们把四个同样的上述三角形构成图4的正方形,这个正方形的边长是
例3
分析与解作为边长为“1”的正方形(图5),它的面积为1,它的
 爱华网
爱华网