两角和正弦公式的精彩证明无字证明集锦 两角和的正弦公式推导

∑(tan(B/2)tan(C/2)+1)cosA=2

一：杨辉三角形

二：整数1所在的位置

三：连续的正整数所在的位置

四：三角形数所在的位置

五：正方形数

六：2的乘方

七：斐波那契数列

八：质数（素数）

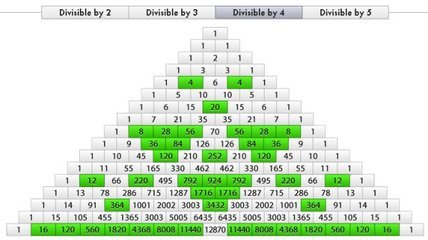
九：偶数所在位置的形状

十：3的倍数所在位置的形状

十一：4的倍数所在位置的形状

十二：5的倍数所在位置的形状

$sin (alpha + beta ) = sin alpha cos beta+ cos alpha sin beta$

$sin alpha cos alpha +sin beta cos beta + 1 times 1 times sin (pi - (alpha +beta ))$

$=2S= (sin alpha + sin beta )(cos alpha+ cos beta ) Rightarrow sin (alpha + beta )= sin alpha cos beta + cos alpha sin beta$

在 $triangleABC$中，成立

$ (tanfrac{B}{2}tanfrac{C}{2}+1)cosA+(tanfrac{C}{2} tanfrac{A}{2}+1)cosB+(tanfrac{A}{2} tanfrac{B}{2}+1)cosC=2.$

∑(tan(B/2) tan(C/2)+1)cosA=2

在 $triangle ABC$ 和$triangle A'B'C'$中，成立

$ sin(A+A') + sin(B+B') +sin(C+C') =4sinfrac{A+A'}{2}sinfrac{B+B'}{2}sinfrac{C+C'}{2}.$

$frac{cosalpha+sinalpha}{cosalpha-sinalpha}+frac{cosalpha-sinalpha}{cosalpha+sinalpha}=2tan2alpha.$

爱华网本文地址 » http://www.aihuau.com/a/25101014/200867.html