10高考自招复习推荐·数学小品
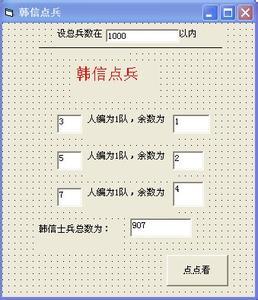
韩信点兵算法及其原理
【问题】求最小非负整数N,使他在除以3,5,7以后所得余数分别是a,b,c。
【韩信点兵法的口诀】
【韩信点兵法口诀的释义】
前三句意思较为明确,假如说一个非负整数N,在除以3,5,7以后所得余数分别是a,b,c。那么70a+21b+15c一定是符合题意要求的数。
第四句“除”字作“减”字解。因为符合要求的最小数N必满足0≤N<105,但是70a+21b+15c却有可能大于105,甚至大于210,所以还不一定是符合要求的最小数。那么当他大于或等于105时,还必须减去105,可能还要再减去105,直到比105小为止,才可以得到符合题意要求的最小数。
【说明】这里105是3,5,7的最小公倍数,70a+21b+15c + 105k也一定满足“除以3,5,7以后所得余数分别是a,b,c”。
【例如】a=b=c=2,70a+21b+15c=212,70a+21b+15c-105=107>105。
而符合题意要求的最小数是 2,即 212-105-105=2.
【再如】 a=2,b=4,c=6,70a+21b+15c=314,314-105=209>105。
而符合题意要求的最小数是 104,即 314-105-105=104.
【韩信点兵法口诀的原理】
①能被5,7除尽数是35k,其中k=2,即70除3正好余1,70a 除3正好余a。
②能被3,7除尽数是21k,其中k=1,即21除5正好余1,21b 除5正好余b。
③能被3,5除尽数是15k,其中k=1,即15除7正好余1,15c 除7正好余c。
这样——
根据①可知 70a+21b+15c 除3正好余a。
根据②可知 70a+21b+15c 除5正好余b。
根据③可知 70a+21b+15c 除7正好余c。
【韩信点兵法口诀的局限性】只适宜于如题所示的一个极为特殊的问题,要推广到同类问题必须另行制作口诀(即公式)。
【譬如】求最小非负整数N,使他在除以5,7,11以后所得余数分别是a,b,c。
【韩信点兵法口诀的原理】
①能被7,11除尽数是77k,其中k=3,即231除5正好余1,231a 除5正好余a。
②能被5,11除尽数是55k,其中k=6,即330除7正好余1,330b 除7正好余b。
③能被5,7除尽数是35k,其中k=6,即210除11正好余1,210c 除11正好余c。
那么 231a+330b+210c除以5,7,11以后所得余数一定分别是a,b,c。
根据【符合要求的最小数N必满足0≤N<385】,所以当 231a+330b+210c大于或等于385时,还必须减去若干个385 直到比385小为止,才可以得到符合题意要求的最小数。
【说明】这里385是5,7,11的最小公倍数,231a+330b+210c + 385k也一定满足“除以5,7,11以后所得余数分别是a,b,c”。
【例如】求最小非负整数N,使他在除以5,7,11以后所得余数分别是3,5,7。
【解】231a+330b+210c=231×3+330×5+210×7=3813.
因为3813>385,所以减去9个385后,得到比385小的 3813-9×385=348就是符合题意的最小非负整数了。
相关链接:10高考自招数学复习推荐试题10510高考自招数学复习推荐试题104:三角形数表10高考自招数学复习推荐试题103:求质数10高考自招数学复习推荐试题102:求整数陈年老题,陈年老错,怎么办?10自招推荐数学复习试题:求人数10自招数学复习推荐试题:比大小10自招推荐数学试题:跳格子中学数学:解答关于函数不动点、稳定点的一个问题数学小品:拼图游戏数学小品:用严格数学计算来判断视觉误差10高考数学答疑-001:向量问题10高考数学答疑-000.开场白高考数学答疑快递:组合数高考数学答疑特快专递:摸球概率高考紧急答疑:立体几何三棱锥高考紧急答疑:向量线性运算中考数学答疑:公交车至少应该设几个座位?高考数学答疑:超越不等式之解高考数学答疑:概率知识使将军赢得一场赌局高考数学答疑:函数绝对值的最大值高考数学试卷压轴题/一类求数列通项问题(之三)高考数学试卷压轴题/一类求数列通项问题(之二)高考数学试卷压轴题/一类求数列通项问题(之一)数学答疑:红黄绿交通信号灯能发的信号数量高考数学答疑:不定方程有无穷多组解的证明高考数学答疑:高速公路车速与车距的解答高考数学压轴题“猜测结论不用证明”是忽悠人高考数学题推荐:高速公路车速问题高考数学选择题:公转与自转问题高考数学填充题:蚂蚁爬行的最短路径高考数学答疑:公转与自转问题高考答疑:蚂蚁应该怎样走,才可以使路径最短解答“正方体体积最大的内接圆锥体”高考数学答疑:“正方体内接圆锥体”问题高考数学“向量运算,几何轨迹”的综合问题的解答高考数学答疑:向量运算,几何轨迹,综合题用数列极限来定义无限连分数的值 爱华网
爱华网