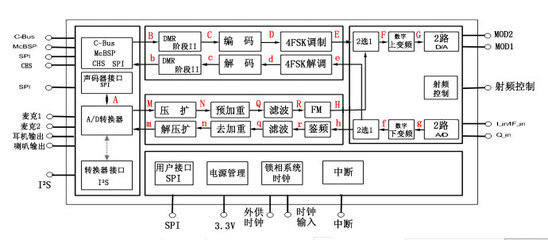
一款分解质因数的软件
最近偶然需要把一个19位数分解质因数,于是到网上去找现成的计算程序,结果令人失望。找到了几个,其中最好的一个限时收费,但却只能分解至16位数;其余的最多只能有效分解9位数,而且运算速度慢得像蜗牛。
没办法,只好自己来做。做成的结果是:可以有效分解27位数,在16
位数以内计算速度不输于下载的那个最好的限时收费的东东。看来,一切都挺好。但接下来就有问题了,原来,随着被分解数位的增加,计算所需的时间增长更快。下面是几条测试记录:
(1)10位数:9999999999 = 3^2 × 11× 41 ×271 × 9091
耗时0.00分
(2)16位数:9999999999999999= 3^2 × 11 ×17 × 73× 101 ×137 × 5882353
耗时0.48分
(3)20位数:99999999999999999999= 3^2 × 11 ×41 × 101× 271 ×3541 × 9091 × 27961
耗时46.96分
(4)21位数:99999999999999999999 = 3^2× 11 ×41 × 101× 271 ×3541 × 9091 × 27961
耗时172.40分
从以上记录可以看出,对21位以上的数进行测试已经没有意义,因为那耗时将不是我们可以接受的时间。
原本我以为高耗时是因为所给的算法不够好,于是绞尽脑汁构思了一个“更优”算法,上机去试,那知道这个“更优”其实“更劣”——当分解20位数时,“优化”后的程序比“优化”前其耗时硬是增加了10分钟以上!看来,未“优化”的算法有可能就是最优的。
进入一些算法论坛去打探,才知道这个问题没有好的解决办法。一旦被分解数超过16位,高耗时将是不可避免的。除非,我们的计算机有了更高端的硬件——我想。
这样的结果也就彻底打消了我的一个念头:去做位数更多的质因数分解程序,使可分解数的位数达到数万位。我自信这样的程序在算法上并无原则困难,但对PC机而言却毫无意义,因为其计算耗时可能会以天、月来计!
鉴于对大整数的质因数分解在密码设计中有着极为重要(或许是第一重要)的位置,我想必然应该已经有现成的大整数质因数分解的程序了,但这样的程序只能在巨型机上运行。
在这篇文章写完之际,我忽然有了一个新的想法:事先制作一个已知素数的数据库,我们的程序在运行中调用这数据库中的数据,如此将会几十倍甚至百倍地提高计算速度。而这样的数据库的制作并不很困难。
不过,如此的方案在大幅度节省时间的同时,程序本身的结构却会复杂起来,并且在运行中将会占用更多的空间资源——这很像当年抗日战争时白崇禧所说的“以空间换取时间”。呵呵,这倒挺有趣……
 爱华网
爱华网