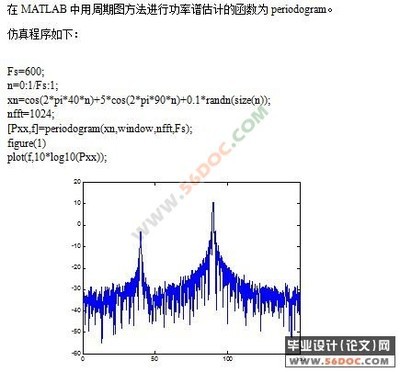
功率谱估计是数字信号处理的主要内容之一,主要研究信号在频域中的各种特征,目的是根据有限数据在频域内提取被淹没在噪声中的有用信号。下面对谱估计的发展过程做简要回顾:
英国科学家牛顿最早给出了“谱”的概念。后来,1822年,法国工程师傅立叶提出了著名的傅立叶谐波分析理论。该理论至今依然是进行信号分析和信号处理的理论基础。
傅立叶级数提出后,首先在人们观测自然界中的周期现象时得到应用。19世纪末,Schuster提出用傅立叶级数的幅度平方作为函数中功率的度量,并将其命名为“周期图”(periodogram)。这是经典谱估计的最早提法,这种提法至今仍然被沿用,只不过现在是用快速傅立叶变换(FFT)来计算离散傅立叶变换(DFT),用DFT的幅度平方作为信号中功率的度量。
周期图较差的方差性能促使人们研究另外的分析方法。1927年,Yule提出用线性回归方程来模拟一个时间序列。Yule的工作实际上成了现代谱估计中最重要的方法——参数模型法谱估计的基础。
Walker利用Yule的分析方法研究了衰减正弦时间序列,得出Yule-Walker方程,可以说,Yule和Walker都是开拓自回归模型的先锋。
1930年,著名控制理论专家Wiener在他的著作中首次精确定义了一个随机过程的自相关函数及功率谱密度,并把谱分析建立在随机过程统计特征的基础上,即,“功率谱密度是随机过程二阶统计量自相关函数的傅立叶变换”,这就是Wiener—Khintchine定理。该定理把功率谱密度定义为频率的连续函数,而不再像以前定义为离散的谐波频率的函数。
1949年,Tukey根据Wiener—Khintchine定理提出了对有限长数据进行谱估计的自相关法,即利用有限长数据估计自相关函数,再对该自相关函数球傅立叶变换,从而得到谱的估计。1958年, Blackman和Tukey在出版的有关经典谱估计的专著中讨论了自相关谱估计法,所以自相关法又叫BT法。周期图法和自相关法都可用快速傅立叶变换算法来实现,且物理概念明确,因而仍是目前较常用的谱估计方法。
1948年,Bartlett首次提出了用自回归模型系数计算功率谱。自回归模型和线性预测都用到了1911年提出的Toeplitz矩阵结构,Levinson曾根据该矩阵的特点于1947年提出了解Yule-Walker的快速计算方法。这些工作为现代谱估计的发展打下了良好的理论基础。
1965年,Cooley和Tukey提出的FFT算法,也促进了谱估计的迅速发展。
现代谱估计主要是针对经典谱估计的分辨率差和方差性能不好的问题而提出的。现代谱估计从方法上大致可分为参数模型谱估计和非参数模型谱估计两种,前者有AR模型、MA模型、ARMA模型、PRONY指数模型等;后者有最小方差方法、多分量的MUSIC方法等。
ARMA谱估计
线性系统可以用线性差分方程进行描述,这种差分模型就是自回归----滑动平均模型(AutoRegression----Moving Average,ARMA )。:任何一个有理式的功率谱密度都可以用一个ARMA随机过程的功率谱密度精确逼近。??ARMA模型定义若离散随机过程{x(n)}服从线性差分方程x(n)+Ai*x(n-i)=e(n)+Bj*e(n-j) 式中i=1,2,...p;j=1,2,...q;e(n)是一离散白噪声,则称{x(n)}为ARMA过程,而上式称为ARMA模型。系数和分别称为自回归(AR)参数和滑动平均(MA)参数,而p和q分别叫做AR阶数和MA阶数。显然,ARMA模型描述的是一个时不变的线性系统。??具有AR阶数p和MA阶数Q的ARMA过程常记作用ARMA(p,q)。
扩展阅读:
张贤达<数字信号处理>--清华大学出版社
第五章功率谱估计
§5.1 引言
从第一章的讨论中,我们已经知道一个随机信号在各时间点上的值是不能先验确定的,它的每个实现(样本)往往是不同的,因此无法象确定信号那样可以用数学表达式或图表精确地表示它,而只能用它的各种统计平均量来表征它.其中,自相关量作为时移的函数是最能较完整地表征它的特定统计平均量值.而一个随机信号的功率谱密度(函数),正是自相关函数的傅氏变换.对于一个随机信号来讲,它本身的傅氏变换是不存在的,只能用功率谱密度来表征它的统计平均谱特性.因此功率谱密度是一个随机信号的一种最重要的表征形式.我们要在统计意义下了解一个随机信号,就要求知道(或估计)的它功率谱密度.
如果我们用表示随机信号的自相关函数,表示它的功率谱密度(以下简写成PSD),则有[见式(1.56)]
(5.1)
而其中
(5.2)
对于平稳随机过程,根据各态历经假设,集合的平均可以用时间的平均代替,于是上式可写成
(5.3)
将式(5.3)代入式(5.1)得
令,上式可写成
(5.4)
式(5.4)在的极限情况下是不可能收敛的,这是因为对于无限时域的随机信号,它的傅氏变换是不存在的.实际上只有将式(5.4)求平均,成为
(5.5)
才有意义[1].正如我们在§1.3中所讨论的:一个无限长的过程的功率谱的概论就是统计平均功率谱.以后我们还将会看到,只有将式(5.4)经过求平均(或平滑),即只有式(5.5)才能满足一个正确的估计必须满足的一致估计的条件.
由于实际得到的随机信号只能是它的一个实现或一个样本序列的片段,因此问题是如何根据它的有限个样本序列来估计信号的自相关函数或功率谱密度.这是本章要讨论的中心内容.当我们用一个样本的记录的有限个数据来估计自相关函数和功率谱密度时,有[参见第一章式(1.48)]
(5.6)
(5.7)
这里
(5.8)
RN为矩形函数,
或按式(5.4)
(5.9)
这里是有限长序列的傅氏变换.
一个好的估计应该是①无偏估计,②最小方差估计.如果我们用表示某个随机变量的真值,表示它的估计值,则希望满足:
(1) 无偏估计
无偏估计,即的偏倚(Bias)为零所谓偏倚(用B表示)定义为
(5.10)
无偏估计即B=0,的估计.图5.1中的估计1和估计2都属于无偏估计.
(2) 最小方差估计
最小方差估计,即方差
(5.11)
为最小的估计.图5.1中,估计2较之估计1方差小.
图5.1 二种估计的概率密度分布
但是常常发生这种情况,一种估计的偏倚较小,而方差较大;另一种估计偏倚较大而方差较小;此时很难定哪一种估计好.因此也常常用均方误差的大小来衡量估计的优劣.在第二章中我们已经讨论到均方误差定义为
(5.12)
利用式(5.10)与式(5.11)的关系不难证明
(5.13)
均方误差为与偏倚和方差均有关,要最小就要求B2与之和最小.
比较式(5.3)与式(5.6)可见,当时式(5.6)就成为式(5.3).因此应有
这就是说,当观察到的样本的数据有无限多个时,按照无穷多个这样的样本数据估计到的自相关函数应该就是自相关函数的真值(各态历经假设).换句话说,一个正确的估计应有
(5.14)
满足式(5.14)的估计称为一致估计.一个正确的估计应该满足一致估计的条件(这是正确估计的必要条件,不是充分条件).反之,如果某种估计方法不能满足式(5.14)一致估计的条件,则这种估计方法一定是不正确的.下面我们在讨论各种估计方法时,常常以此作为估计正确与否的主要准则之一.
功率谱估计有着极其广泛的应用,不仅在认识一个随机信号时,需要估计它的功率谱.它还被广泛地应用于各种信号处理中.下面我们举三个应用的例子.
① 在信号处理的许多场所,要求预先知道信号的功率谱密度(或自相关函数).例如,在最佳线性过滤问题中,要设计一个维纳滤波器就首先要求知道(或估计出)信号与噪声的功率谱密度(或自相关函数).根据信号与噪声的功率谱(或)才能设计出能够尽量不失真的重现信号,而把噪声最大限度抑制的维纳滤波器(见第二章).
② 常常利用功率谱估计来得到线性系统的参数估计.例如,当我们要了解某一系统的幅频特性时,可用一白色噪声通过该系统.再从该系统的输出样本y(n)估计功率谱密度.由于白色噪声的PSD(用表示)为一常数即,于是按照式(1.67)有
故通过估计输出信号的PSD,可以估计出系统的频率特性(模特性).
在下面将要讨论到用自回归模型法估计PSD的一节中,我们将要具体讨论系统参数估计与PSD估计间的关系.
③ 从宽带噪声中检测窄带信号.这是功率谱估计在信号处理中的一个重要用途.但是这要求功率谱估计有足够好的频率的分辨率,否则就不一定能够清楚地检测出来.所谓谱估计的分辨率可以粗略地定义为能够分辨出的二个分立的谱分量间的最小频率间隙(距).例如有一个随机信号,它包括二个频率相差1Hz振幅相等的正弦波以及加性白噪声(白色噪声的方差是正弦波功率的10%).图5.2表示用三种不同的谱估计方法检测这二个正弦分量的效果.图中(a)是用经典法(BT PSD);(b)是用最大熵谱估计法(即自回归PSD法):(c)是用Pisarenko谐波分解法.由图可见,(c)的分辨率最好,(a)的分辨率最差,(b)的分辨率在(a)与(c)之间.用(a)的方法就无法检测出这二个正弦波分量.因此提高谱估计的分辨率已成为目前谱估计研究中的一个重要方向.
图5.2 三种不同分辨率的谱估计方法的例子
(a) 经典法BT PSD法;(b) 最大熵谱估计法(自回归PSD法);(c) Pisavcnko 谐波分解法.
谱估计问题论从认识一个随机信号或从其它应用方面来讲都是重要的.因此对谱估计方法的研究引起了国内外学者的广泛注意与重视.它是当前在信号处理中的一个十分活跃的课题.
本章我们将分节讨论功率谱估计的几种主要方法和它们的特点.总的来讲可以分成经典谱估计法与现代谱估计法.经典法实质上就是传统的傅氏分析法,它又可分成二种.一种是间接的方法,它先通过式(5.6)对自相关函数进行估计(一般都需要窗函数将自相关值加权,以减小自相关序列截段的影响),然后再通过式(5.7)作傅氏变换得功率谱估计值.这种方法是1958年由Blackman与Tukey提出的,简称BT PSD估计法.另一种是直接法,它是将观察到的有限个样本数据利用FFT算法作傅氏变换直接按式(5.9)进行功率谱估计(不通过自相关函数的估计),这种方法称为周期图法.本章的经典法中主要讨论周期图法.
这种用周期图(包括平滑后的周期图)作为功率谱估计的方法可利用FFT进行计算,因而有计算效率高的优点,在谱分辨率要求不高的地方常用这种周期图法进行谱估计.它的一个主要缺点是频率分辨率低.这是由于周期图法在计算中把观察到的有限长的N个数据以外的数据认为是零.这显然与事实不符合.把观察不到的值认为是零,相当于将x(n)在时域里乘上了一个矩形窗口函数,这在频域里相当于张了一个与之卷积的sinc函数,由于sinc函数与函数比较有二方面的差别,其一是其主瓣不是无限窄,其二是有旁瓣,因此卷积的结果必然造成失真.由于主瓣不是无限窄,如果原来真实的功率谱是窄的,与主瓣卷积后将使功率向附近频域扩散,使信号模糊,降低了分辨率,主瓣愈宽分辨率愈差.由于存在旁瓣,又将产生两个后果,基一是PSD主瓣内的能量"泄漏"到旁瓣将使谱估计的方差增大,其二是与旁瓣卷积得到的信号功率谱完全属于干扰.在严重的情况下,强信号与旁瓣的卷积可以大于弱信号与主瓣的卷积,使弱信号淹没在干扰的强信号中,而无法检测出来.这正是周期图作为功率谱估计的二个主要缺点.
对于BT PSD估计法,由于它是按式(5.7)将功率谱用有限个自相关函数值的傅氏变换代表按式(5.1)用无限个自相关函数值的傅氏变换求得的真实功率谱.这相当于将序列乘上了一个矩形窗口函数,因此也同样存在上述二个缺点.许多学者想尽办法,企图选择适当窗口函数的形状来提高经典法的谱分辨率,但是发现,所有能降低旁瓣的窗口函数都是以主瓣的增宽为代价的;反之亦然.这两个缺点只能互换而无法同时改善.因此用经典法无法克服谱分辨率的缺点.为此近几年来,在提高功率谱估计的分辨率方面提出了很多新的方法.
以1967年Burg提出的最大熵谱分析法为代表的现代谱估计法,不认为在观察到的N个数据以外的数据全为零.因此克服了经典法的这个缺点,提高了谱估计的分辨率.后来发现线性预测自回归模型法(简称AR模型法)与Burg的最大熵谱分析法是等价的,它们都可归结为通过Yule-Walker方程求解自回归模型的系数问题.目前常用的求自回归模型系数的算法有三种:①为Levinson递推算法;②为Burg递推算法;③为正反向线性预测最小二乘算法.除了最大熵谱分析法(包括线性预测AR模型法)外近年来出现了许多适用于不同情况的提高谱估计分辨率的新方法,如模型法中还有滑动平均(MA)模型法与自回归滑动平均(ARMA)模型法,另外还有Pisarenko谐波分解法,Prony提取极点法,Prony谱线分解法以及Capon最大似然法等等.这些近代谱估计法,本章主要讨论最大熵谱分析法(包括线性预测AR模型法),它是目前用得最多的一种高分辨率的谱估计方法.
§5.2 自相关函数的估计
设观察到N个样本序列的值:.现在要由此N个数据来估计自相关函数.由于只能观察到的N个值,而时的值是不知道的,因此,式(5.6)成为
(5.15)
式中 m取绝对值是因为,m为负值时上式仍适用.式(5.15)规定的求和上下限的原则是保持充分利用全部(N个)数据.这种估计方法的效果如何,我们首先需要看它的偏倚与方差是否满足一致估计的条件.
由式(5.15),得
所以
故这种估计,当时,属于无偏估计.
现在来求,按定义
(5.16)
又按式(5.15)
(5.17)
当随机序列是零均值,实,高斯序列时,有
所以
代入式(5.17),得
代入式(5.16),得
令,显然的最小值为,最大值为,且的情况将出现次,的情况将出现次以此类推,对不同值的情况,出现的次数将为,于是上式可写成
(5.18)
当N》m时,上式以1/ N趋趋于零,即.故的方差满足一致估计的条件.如果不是高斯过程,在上式中需要再加一项,但此项往往是可以忽略的,因此,式(5.18)仍近似适用.
式(5.15)这种估计自相关函数的方法,虽然当m很小于N时能得到一致估计,但当N一定时,就变得十分大,因而不能得到有用的估计.因此很多学者如Jenkins-Watts[27]和Parzen[1]等都主张按下式估计,我们用表示
(5.19)
同时
这相当于它的均值等于真值用三角窗函数加权.故是有偏的,其偏倚为
同时
事实上,将用三角窗函数加权后,不仅使方差减小,而且有利于钝化的截段边界使的卷积因子从sin C函数的形式降低波动,可改进对的估计.
虽然的Bias和Var都不等于零,但当时为一致估计,且,同时可以证明的均方误差小于的,以及可改进对的估计,所以今后我们还是用作为自相关函数的估计,并仍用表示,即
(5.19)
通过将自相关函数的估计进行傅氏变换求得功率谱估计的方法即为BT PSD法.
§5.3 周期图作为功率谱的估计
将式(5.19)代入(5.7)得
这里的下标N表示它们是有限长(长为N)的序列[见式(5.8)]令l=n+m,有
其中的为
即是有限长序列x(n)的傅氏变换.显然是周期性的.直接将的模的平方除以N求得的功率谱的估计称为周期图,并用表示.于是有
(5.20)
如果我们观察到x(n)的N个值:,可以通过FFT直接求得[频率离散化的].然后按照式(5.20)直接求得(不必先通过估计自相关函数).这种将周期图作为功率谱估计的方法的主要优点是计算方便,它可以直接用FFT算法从x(n)得到.从而得到.正是由于它的这个优点,使这种方法成为一种十分通用的方法.
为了了解周期图作为功率谱估计的估计效果,让我们来讨论它的偏倚和方差.为此首先需要求周期图的期望值.
按式(5.19),得
(5.21)
这里RN代表矩形序列.
令
(5.22)
由于是二个矩形函数的卷积,因此它必是一个三角函数,常常称它为Bartlett窗函数,用表示,不难证明
(5.23)
而它的傅氏变换为
(5.24)
又 自相关函数的真值
将上式与式(5.22)代入式(5.21),并求其傅氏变换,得
(5.25)
由式(5.25)可见,除非为函数,将不等于,故周期图作为的估计是有偏的:
当时
故
(5.26)
因此,周期图作为功率谱的估计,当时是无偏的.
为了得到周期图的方差,首先假设序列是一个实,白色,零均值过程的样本,具有高斯概率分布函数.按方差的定义应有
(5.27)
按式(5.20),周期图可表示为
将关系
代入上式,并求期望值:
(5.28)
其中
由于我们假设是白色的,所以代入上式得
(5.29)
为了求得,按式(5.27)除了需要求得以外,还需要求得,为此我们先求在频率为的协方差,参照式(5.28)可得
(5.30)
对于白色高斯过程可以证明(见参考文献[3])
(5.31)
考虑到对于白色过程有所以
(5.32)
代入式(5.30)得
(5.33)
上式当n=k及p=q时只有第一项存在(其它二项为0);当n=p及k=q时只有第二项存在;当n=q,k=p时,只有第三项存在.
又因为
故式(5.33)成为
(5.34)
而其中
同理可得
代入式(5.34)得
(5.35)
当时得
故有
(5.36)
由工式可见,当,.这说明周期图不满足一致估计的条件.不论N取多长,都有的量级.因此周期图不是对功率谱的好的估计.实际上当时式(5.20)成为式(5.4).正像我们在讨论式(5.4)时所指出的,对于无限能量的随机序列,它的傅氏变换是不存在的,因此式(5.4)在的极限情况下是不可能收使用的.故也就不能期望当时会等于它的真值,而满足一致估计的条件.为了使周期图作为功率谱估计满足一致估计的条件,我们必须将周期图进行平滑(或平均)处理.
如果我们需要求周期图的协方差,则有
(5.37)
如果以及(k和l为整数)则上式成为
上式在以及不是N的整倍数时等于零.因此以的整倍数为频率间距的周期图的值是不相关的,当N增大时,协方差为零的功率谱样本之间的间距减小.因此可以预料到N增加将会使周期图的起伏增快.图5.3说明了周期图的这种特性.图(a),(b),(c)分别表示N为16,32和64时的周期图.
(5.38)
及
虽然本节推导的结果是以假设高斯概率密度为根据的,但其定性结果在一个相当宽广的范围内成立.
图5.3 高斯白噪声序列的周期图
§5.4 平滑后的周期图作为PSD的估计
上面我们已证明周期图作为功率谱的估计不满足一致估计的条件.因为当,方差,因此必须作一些修正.
本节将表明如果将周期图进行平滑(平均是一种主要的平滑方法)将会使方差减小,得到一致地谱估计.平滑的主要方法有二种.在FFT出现并广泛应用以前主要用窗口处理法进行平滑,即选择适当的窗口函数作为加权函数进行加权平均来加快收敛速度.另一种平滑方法是平均周期图的方法,即先将数据分段,再求各段周期图的平均值.后一种方法又称为Bartlett方法,是当前用得最多的一种平滑方法.Welch又对Bartlett方法进行了改进并提出了用FFT计算的具体方法.
5.4.1 巴特利特(Bartlett)平均周期图的方法
首先让我们来看一下为什么周期图经过某种平均(或平滑)后会使它的方差当时趋于零,达到一致估计的目的.
如果是不相关的随机变量,每一个具有期望值,方差,则可以证明它们的数学平均的期望值等于,数学平均的方差等于,即
所以
(5.40)
(5.40)可见,L个平均的方差比每个随机变量的单独方差小L倍.当,可达到一致谱估计的目的.因而降低估计量的方差的一种有效方法是将若干个独立估计值进行平均.把这种方法应用于谱估计通常归功于Bartlett.
Bartlett平均周期图的方法是将序列分段求周期图再平均.设将分成L段,每段有M个样本,因而,第i段样本序列可写成
第i段的周期图为
如果很小,则可假定各段的周期图是互相独立的.按照§5.4对功率谱密度的概念的讨论,谱估计可定义为L段周期图的平均,即
(5.41)
于是它的期望值为
将式(5.25)与式(5.24)代入上式得
(5.42)
这里,因此Bartlett估计的期望值是真实谱与三角窗函数的卷积.由于三角窗函数不等于函数,所以Bartlett估计也是有偏估计即,但当时,.
由于我们假定各段周期图是相互独立的,所以可按式(5.40)得到下式:
(5.43)
由此可见,随着L的增加是下降的,当时,.因此Bartlett估计是一致估计.
比较式(5.42)的与式(5.25)的可见在二种情况的估计量的期望值都是真值与窗口函数的卷积形式,但后者将前者WB中N改为M,.因而使主瓣的宽度增大.由于主瓣的宽度愈窄愈接近函数,偏倚愈小.今式(5.42)中的主瓣宽度大于式(5.25)中的主瓣宽度,因而,而主瓣愈宽显然使分辨率愈差.因此Bias可用来说明谱的分辨率,Bias愈大说明谱分辨率愈差.一个固定的记录长度N,周期图分段的数目L愈大将使方差愈小,但M也愈小,因而使Bias愈大,谱分辨率变得愈差.因此Bartlett方法中Bias或谱分辨率和估计量的方差间是有互换关系的.M和N的选择一般是由对所研究的信号的预先了解来指导的.例如,如果我们知道谱有一个窄峰,同时如果分辨出这个峰是重要的,那么我们必须选择M足够大.又从方差的表达式我们可以确定谱估计的可接受的方差所要求的记录长度.
由此可见Bartlett法使谱估计的方差减小是用增加Bias以及降低谱分辨率的代价换来的.实际上,当N一定时,Bias与Var的互换性是谱估计的一个固有特性.
[例如] 为了说明经平均后的周期图作为功率谱估计的实际效果,设有一零均值高斯分布的随机过程,其功率谱密度为
这一功率谱密度是由一零值高斯分布单位方差的噪声序列通过一个其的滤波器形成的.为了简单设选用的矩形窗函数.其周期图的期望值(用表示)与真值均表示在图5.4中.它说明的周期图可以得到的Bias的情况.图5.5表示分4段与16段二种情况平均后的周期图.显然L=4的方差比L=16的大.将L=16的曲线与图5.4的曲线比较可见在这种估计中误差的大部分起因于Bias而不是方差(因为二种情况均为,Bias相仿,误差也相仿).M=16,L=2及8的周期图表示在图5.6.图5.6中L不同造成的影响也是明显的.但是这二个曲线的起伏都很大,因此有理由认为误差主要起因于方差.比较与M=16的周期图可见,在§5.3中得到的M愈大(即§5.3中的N愈大),将使周期图的起伏愈增快的结论,在这里也同样成立.
比较图5.5与图5.6发现在这个例子中最好的选择是应用L=16,的估计而不是L=8,M=16的估计,即宁可减小方差,牺牲Bias.在实际中,当然功率谱密度的真值是不知道的.但是谱的窗口函数以及关于功率谱密度的某些信息往往是预先知道的.通过改变M和L以及利用预先知道的情况,通常可以很好地进行选择.
平均周期图的方法特别适合于应用FFT算法.因此在FFT出现以后这个方法比下面将要讨论的利用窗口函数的处理法用得更多.而在FFT出现以前主要是用窗口函数处理法平滑周期图.
图5.4 与的特性 图5.5 平滑后的周期图(每段取8个数据)
图5.6 平均后的周期图(每段取16个数据)
5.4.2 窗口处理法平滑周期图
平滑周期图的另一种常用的方法,是用一合适的窗口谱函数与周期图卷积,即
(5.44)
或 (5.45)
这里与分别是与的傅氏反变换,并设序列长2M-1.在第一章中我们已讲话到是一个实,偶,非负函数,应是一个偶序列,并且满足条件:
(5.46)
例如前面用到的三角或Bartlett窗函数是满足此条件的,而海宁(Hanning)与汉明(Hamming)窗函数就不满足式(5.46)的条件[2]虽然这后二种窗函数能够提供较好的频率分辨率以及较低的旁瓣,但会产生负的功率谱估计.
如果我们将时域与频域对换,由式(5.44)的卷积形式,可以看成是通过一个具有"单位样本响应"的滤波器产生的.的"频率响应"具有低通特性,因此可以平滑,对中快变化成分有滤除作用,因此我们称为平滑后的周期图.
因式(5.44)可得
(5.47)
又按式(5.25),有
(5.25)
因式,有
(5.48)
这里
现在如果M比N小得多,则,于是式(5.48)可近似写成
(5.49)
将式(5.49)与式(5.25)比较可见,如将式(5.25)右边的换成,则式(5.25)就全同于式(5.49).事实上,由于周期图法是将观察到的x(n)的N个以外的值均认为是零,这实际上已把x(n)乘上了一个矩形窗口(即使我们并没有作窗口处理).式(5.25)中的三角窗函数正是这个矩形窗口造成的,加窗口处理后将式(5.25)改变成式(5.49).等于将式(5.25)中的窗函数改变成.
如果的主瓣宽度大于的主瓣宽度,则可进一步平滑谱估计,减小谱估计的方差,但是同样带来Bias的半加和谱分辨率的变差.至于选用怎样的窗口函数才能用较少的Bais的增加与分辨率的降低来换取较多的谱估计的方差的改善以及窗口处理对谱估计方差的影响的具体研究请参考文献[2],[3],这里不再讨论.
5.4.3 Welch法
Welch提出了对Bartlett法的修正使更适合于用FFT进行计算.他主要提出二方面的修正,其一是选择适当的窗函数,并在周期图计算前直接加进法,这样得到的每一段的周期图为
(5.50)
这里为归一化因子,而Bartlett法每段的周期图为
(5.51)
这样加窗函数的优点是无论什么样的窗函数均可使谱估计非负.其二是在分段时,可使各段之间有重迭,这样将会使方差减小(当N与M一定时).他建议可以重迭50%.Welch法具体在计算上的改进,请参阅文献[29].
§5.5 自回归模型法
在§5.5节中我们讨论到经典法是按照观察到的N个样本值,估计功率谱的,它实际上是认为在此观察到的N个数据以外的x(n)=0,显然这是与实际不符合的,因而导致了种种缺点.
如果我们能根据这些已观察到的数据,选择一个正确的模型,认为x(n)是白噪声通过此模型产生的,那么就不必认为N个以外的数据全为零了.这就有可能得到比较好的估计.这种方法可以分下列几个步骤进行.
(1) 选择一个模型.
(2) 用已观察到的样本数据或自相关函数的数据(如果已知或可以估计出)来确定模型参数.
(3) 由此模型求PSD.
在实际中我们所遇到的随机过程,常常总是可以用一个具有有理分式的传递函数的模型来很好地表示它,因此可以用一个线性差分方程作为产生随机序列x(n)的系统的模型:
(5.52)
这里表示白色噪声,将上式变换到z域则有
该模型的传递函数为:
(5.53)
其中
(5.54)
当输入的白噪声的功率谱密度为时,输出的功率谱密度为
(5.55)
将代入上式得
(5.56)
如果能研究各ak及bl就可求得
设,并不会影响式(5.52)与式(5.53)的一般性.现在如果除b0=1外的所有bl均为零.则式(5.52)成为:
(5.57)
式(5.57)的形式使它被称为p阶自回归模型简称AR(Autoregressive)模型.将式(5.57)进行z变换,可得AR模型的传递函数为
(5.58)
自回归模型的H(z)只有极点,没有除原点以外的零点,如图5.7所示.因此又称为全极点模型.当我们采用自回归模型时,式(5.56)成为
(5.59)
此时,只要我们能求得所有ak参量,就可求得.
图5.7 自回归模型
现在如果式(5.52)中除a0=1的所有ak均为零,则式(5.52)成为
(5.60)
式(5.60)的形式使它称为q阶动平均模型,简称MA(Moving Average)模型.MA模型的传递函数为
(5.61)
MA模型的H(z)只有零点没有除原点以外的极点,因此又称为全零点模型.当我们用MA模型时,式(5.56)成为
(5.62)
此时,只要我们能求得与所有的bl参量,就可求得.
当均不完全为零时的模型称为ARMA模型.式(5.52)和式(5.53)分别表示了ARMA模型的差分方程与传递函数.
由以上的讨论可见,用模型法作功率谱估计,实际上要解决的是模型的参数估计问题.
Wold分解定理(参见文献[1])告诉我们任何有限方差的ARMA或MA平移过程可以用可能是无限阶的AR模型表达;同样,任何ARMA或AR模型可以用可能是无限阶的MA模型表达.因此,如果在这三个模型中选了一个与信号不匹配的模型,利用高的阶数仍然可以得到好的逼近.由于对AR模型参数的估计,如下面将要看到的,得到的是线性方程.故AR模型比ARMA以及MA模型有在计算上的优点.同时,实际的物理系统往往是全极点系统.所以研究有理分式传递函数的模型,主要研究AR模型.本节也只讨论AR模型.
下面我们就集中讨论AR模型的谱估计法.
由上面的讨论已经得到有关AR模型的如下几个方程:
(5.57)
(5.58)
(5.59)
为了得到必须求得参数a1, a2, a3, …, ap及为此,让我们来推导这些AR参数与之间的关系.我们将会看到,这个关系正就是§2.4中的Yule-Walker方程.
按定义
将式(5.57)的关系代入上式,得
(5.63)
按式(5.57),x(n)只与相关而与无关,故式(5.63)中的第二项为
代入式(5.63)
或
将m=1,…,p分别代入式(5.64)并写成矩阵形式,得
(5.67)
如果将式(5.35)与式(5.64)合在一起[即式(5.66)]写成矩阵形式,有
(5.68)
式(5.66)及式(5.68)就是Yule-Walker方程.由式(5.66)或(5.68)可解得各ak及.将式(5.66a)与式(2.74a)比较可见,如果二式中的是代表同一个随机信号的自相关函数,则式(5.66a)与式(2.74a)的区别仅仅在于式(2.74a)中的l=1,2,…, p(式(2.74a)中的l相当于式(5.66a)中的m),而式(5.66a)中的m可以取任何大于零的整数,包括1,2,…, p,也包括p的值.如果我们取式(5.66a)的m=1,2,…, p的p个方程(即式(5.68)),解得ak(k=1,2,…, p)的p个参量,则这p个ak必将等于利用式(2.74a)的p个方程解得的p个apk,即
(5.69)
我们再将式(5.66b)与式(2.74b)作比较,由于二式的是代表同一个的自相关函数,又有,故有
(5.70)
于是,式(5.68)全同于式(2.75).
式(5.69)与(5.70)说明,如果一个随机序列x(n)的形成系统是一个p阶的AR模型(即x(n)可由一白噪激励一p阶AR模型产生),形成系统的传递函数为
(5.58)
其功率谱密度为
(5.59)
则其中的ak与分别等于x(n)的p阶线性预测器的系数apk与最小均方误差,因此AR模型法又称为线性预测AR模型法.这种估计功率谱密度的方法可归结为求AR模型的各ak参数的问题,也可以归结为求在最小均方误差准则下的线性预测器的系数apk的问题.
按式(2.70),线性预测误差为
(2.70)
将上式进行z变换,得
于是
(5.71)
由式(5.71)可见,是以x(n)作为输入信号,误差e(n)作为输出信号的滤波器的传递函数,该滤波器称为预测误差滤波器.将式(5.71)与式(5.58)比较,当apk按最小均方误差准则求得时,有apk=ak ,故有
(5.72)
即预测误差滤波器是x(n)的形成系统的逆滤波器,于是,有
(5.73)
即将x(n)送入预测误差滤波器,其输出e(n)等于x(n)的形成系统的激励信号:白噪声,如图5.8所示.因此,如果我们所观察到的x(n)是某一原始信号s(n)与-AR系统的冲击响应h(n)的卷积所形成,即
(5.74)
又如果s(n)是白噪过程,则将此x(n)送入预测误差滤波器,得到的输出
(5.75)
因此,在这种情况下可以利用预测误差滤波器将式(5.74)进行解卷积求得原始信号s(n),这正是预测解卷积的基本思想.
图5.8 AR模型的H(z)与其逆滤波器的串接
预测误差滤波器可以利用横向延时抽头的FIR滤波器实现,也可以利用§5.7将要讨论到的格型滤波器实现.图5.9示出了横向结构的预测误差滤波器.
图5.9 横向结构的预测误差滤波器
由以上讨论的AR模型参数与维纳预测器系数间的关系可以看出,不难用自适应滤波原理求各加权系数的方法来求得自回归模型的各ak参数.
§5.6 最大熵谱估计法
最大熵谱估计法简称为MESE(Maximun Entropy Spectral Estimation)法.我们将分二节(§5.6与§5.6)讨论最大熵谱估计法.本书主要讨论:最大熵谱估计法的基本思想,线性预测AR模型与MESE法的等价性以及Levinson-Durbin算法.预测误差格型滤波器,Burg递推算法以及正反向线性预测最小二乘算法,将留在下一节讨论.
5.6.1 最大熵谱估计法的基本思想及其与线性预测AR模型法的等价性
在前面§5.1中我们已经讨论到经典法(BT PSD法)用已知的有限个(N个)自相关函数序列的估值求功率谱估计时,是将此有限个估值以外的自相关序列的数据认为是零,因而得不到好的分辨率.J.P.Burg于1967年提出的MESE法与此不同,它是基于将已知的有限长度的自相关序列以外的数据用外推法求得,而不是把它们当作是零.如果假设已知问题在于按什么原则外推.在保证自相关函数的Toeplitz矩阵是正定的情况下有无穷多种外推法,Burg认为外推的自相关函数应使时间序列表现出最大熵,因此把Burg提出的这种方法称之为最大熵谱估计法.
我们知道所谓熵是代表一种不定度,最大熵为最大不定度,即它的时间序列最随机,而它的PSD应是最平伏(最白色).按Shannon对熵的定义,当x的取值为离散的时,熵H定义为
(5.76)
这里pi为出现状态i的概率.当x的取值为连续的时,熵被定义为
(5.77)
这里p(x)为概率密度函数.当我们处理时间序列的实现问题时,概率密度应由联合概率密度函数代替.设为零均值,高斯分布的随机过程.一维高斯分布为
(5.78)
其中 (5.79)
N维高斯分布为[28]
(5.80)
其中
(5.81)
这里 (5.82)
下面我们先求一维高斯分布的信号的熵,然后推广到N维.为此将式(5.78)及式(5.79)代入式(5.77)得
因为
代入上式得到一维高斯分布的熵为
(5.83)
同理可求得N维高斯分布信号的熵为
(5.84)
式中代表矩阵的行列式,要使熵H最大,就要求最大.
如果已知现欲求得.由于自相关函数的矩阵必是正定的,故矩阵的行列必大于零,即
(5.85)
为了得到最大熵,要求最大,为此用对上式微分,使,求得使最大的,满足下列方程:
(5.86)
上式是的一次函数,由此式可解出.于是又可以此为已知,再用类似方法求得,以此类推.这样每步都按最大熵的原则外推后一个自相关序列的值,可以外推到任意多个而不必认为它们是零.这就是最大熵谱估计法的基本思想.
可以证明这种按最大熵外推自相关函数的结果与AR模型是等价的.为了证明这一点,将式(5.66a),即
(5.66a)
中的m分别用1, 2, …, N+1代入,写成下列方程组:
(5.87)
(5.88)
式(5.87)即式(5.67)只是把阶数p写成N.如果我们从式(5.87)的N个线性方程中解得的N个AR参数a1, a2,…, aN值,代入式(5.88)并将其整理成行列式的形式,即可得
(5.89)
注意,从AR模型得到的式(5.89)与按最大熵外推得到的式(5.86)完全相同,这就证明了当x(n)为高斯分布时最大熵谱估计法与AR模型法是等价的.
事实上,当x(n)是高斯分布带限(为其最高频率)时间序列,且其功率谱密度满足
时,则可以从式(5.78)出发证明其熵正比于[8],[22][7]
(5.90)
在必须与已知的自相关函数的N+1个值符合的约束条件下,即
(5.91)
的约束条件下,可以利用变分法证明使熵最大的功率谱为[3][7][8][22]
(5.92)
其中与an由下列矩阵方程确定
(5.93)
式(5.93)就是Yule-Walker方程,因此这就直接说明了最大熵谱估计与AR模型等价的.
5.6.2 Levinson-Durbin递推算法
由以上的讨论可见,最大熵谱估计法与线性预测AR模型法是等价的,它们都可归结为求解Yule-Walker方程中的各AR系统ak(k =1,2,…,p)的问题,但是直接从Yule-Walker方程式(5.93)求解参数ak(k =1,2,…,N)需要作求逆矩阵的运算,当N大时,运算量很大,并且每当模型阶数增加一阶,矩阵增大一维,需要全部重新计算.
Levinson-Durbin算法对Yule-Walker方程提供了一个高效率的解法.此算法是按下列递推法进行的:依次求得.注意,附加的a的第一个下标是指AR模型的阶数.最后p阶的解即是所要求的解.递推算法以一阶AR模型(求一阶参数a11及)开始.按式(5.93)一阶AR模型的Yule-Walker矩阵方程应为
从这个矩阵方程可解a11与,分别为
(5.94)
(5.95)
再从二阶AR模型的矩阵方程:
解得a22,a21,分别为
(5.96)
(5.97)
(5.98)
以此类推得递推公式:
(5.99)
(5.100)
(5.101)
于是,当我们从式(5.94)与式(5.95)得到初始的a11与的数据以及各,就可按式(5.99),(5.100),(5.101)依次递推出各阶的akk,aki,.从式(5.101)有,一般来讲阶数预先是不知道的,当我们递推到第k阶,满足所允许的值,就可选阶数p=k.前面已证明这里的就是误差功率.小代表均方误差小.如果信号的正确模型是p阶的AR模型,则应有
(5.102)
这说明已达最小均方误差值
由式(5.101)可见,由于,对于任何k必有
(5.103)
可以证明[1]式(5.103)正是的所有极点均在单位圆内的(即稳定性的)充分必要条件.它也是为正定矩阵的充分必要条件.
§5.7 预测误差格型滤波器及伯格(Burg)递推算法
用Levinson递推算法求解Yule-Walker方程中AR系数虽然可以简化计算,但需要知道自相关序列实际上自相关序列只能从时间序列x(n)的限个数据得到它的估计值.当时间序列短时,的估计误差很大,这将对AR参数ak(k =1,2,…,p)的计算引入很大误差,导致功率谱估计出现谱线分裂与谱峰频率偏移等现象.J.B.Burg在1967年的"最大熵谱分析"一文[5]中提出最大熵谱估计法时只说明了如何从已知的N个外推N个以外的值从而可得到高分辨率的功率谱,但该文并未涉及如何从有限时间序列来得到这个N个的问题.随后,Burg又于另一篇文章中提出一种直接由时间序列计算AR模型参数的方法[1],被人们称为Burg算法,这种算法与预测误差滤波器有密切关系.它是在Levinson关系式(5.100)的约束下,用使前向与后向预测误差能量之和为最小的方法来求得各ak(k =1,2,…,p)的值.
5.7.1 预测误差格型滤波器
按线性预测理论,x(n)的估计值可用x(n)的各过去值的加权之和表示,即
(2.69)
误差e(n),在这里用ep(n)表示(p为阶数)
(5.104)
ep(n)称为线性预测器的前向误差,因为是由x(n)以前的各数据:x(n-1),x(n-2),…,x(n-p)加权之和得到的.由Levinson关系式(5.100)可得
(5.105)
又令,这里的KP称为部分相关系数(PARCOR)或反射系数.将这些关系代入式(5.104)得
(5.106)
这里
所以 (5.107)
这里
(5.108)
是由x(n-p)以后的各数据:加权之和得到的,故bp(n)称为后向预测误差.比较前向预测误差方程(5.104)与后向预测误差方程式(5.107)可见,它们具有相同的系数.
将式(5.105)代入式(5.107),用证明式(5.106):
(5.106)
类似的方法,可以证明
(5.109)
按式(5.104)及式(5.107),当p=0时有
(5.110)
式(5.106)与式(5.109)为前向及后向预测误差的递推公式.由式(5.108),(5.109)及(5.110)可得格型预测误差滤波器,如图5.10所示.由图5.10或式(5.108),(5.109)可见,只要求得Kp,就可以直接从x(n)求得ep(n-p)与bp(n).
图5.10 格型预测误差滤波器
如果将式(5.104)进行z变换,得
于是有
(5.111)
由式(5.111)可见,这里的就是§5.7中的He(z),它是预测误差滤波器的传递函数.因此线性预测误差滤波器可以用横向延时抽头的FIR滤波器实现(如图5.9所示),也可以用格型结构的FIR滤波器实现(如图5.10所示).这二种结构的滤波器在数学关系上是完全相同的,都是由式(5.104)导出,但我们将会看到,由于二者的结构不同,它们有很多不同的性能,从而在实际应用效果上也是不同的.
将式(5.104)与式(5.107)分别写成展开形式,有
(5.104)
(5.107)
比较上二式可见,后向预测误差bp(n)的系数正九是前向预测误差ep(n)的系数在次序上的逆转.因此,如果我们将图5.9的横向结构的预测误差滤波器的输入不是从第一级(最左端),而是从末级(最右端)送入,如图5.11所示,则输出将不是前向误差,而是后向误差,有
(5.112a)
(5.112b)
(5.112c)
这里 (5.108)
如果我们令,于是,式(5.112c)成为
(5.112d)
而其中 (5.113)
将式(5.113)与式(2.69)比较可更清楚的看到,后向预测不是像前向预测那样,用它以前的p个值的线性组合来预测它,而是用它以后的p个值的线性组合来预测它(即式(5.113)右边k前的符号与式(2.69)右边k前的符号相反).
图5.11 后向预测误差
按式(5.111)前向预测误差滤波器的传递函数为
(5.114)
这里,它与He(z)是一对z变换对,因此,如果输入序列,则输出序列.
由式(5.112)可得后向预测误差滤波器的传递函数(用Hb(n)表示)
(5.115)
这里,它与Hb(z)是一对z变换对.将式(5.115)与式(5.114)比较显然有
(5.116)
由式(5.116)可见,当z=z1是Hb(z)的一个零点(或极点)时,则它也将是He(z-1)的一个零点(或极点).因此1/z1将是He(z)的一个零点(或极点).于是,如果He(z)是一个最小相移网络,其零极点全部在单位圆内,则Hb(z)将是一个最大相移网络,其零极点将全部在单位圆外.当时,He(z)将是稳定的和最小相移的,而Hb(z)将是稳定的和最大相移的.
全零点的格型预测误差滤波器是Itakura和Saita于1971年首先提出的.Burg虽然在1967年就提出了有关的方法,但他并没有具体地把格型网络的性质和他的最大熵技术等同起来,现在已经知道Itakura和Burg的方法是更一般的格型概念的特例.
格型结构的FIR滤波器与横向结构的比较有很多优点.在数字滤波器中有二个重要问题:有限字长效应的影响和参数值扰动对滤波器性能的敏感性.在这二点上格型结构的滤波器都优于横向结构的滤波器.由图5.10可见,一个p阶的格型预测误差滤波器是由p级组成,而前面各级的输出,正好依次是各低于p阶的预测误差滤波器的输出.当滤波器各阶输出信号都满足最小均方误差时,并在输入信号是平稳的情况,可以证明,格型预测误差滤波器前后各级的输出误差之间的正交的,这种正交性可以用数学表达式表示如下[10]:
(5.117)
(5.118)
这里是第m阶的预测误差能量.这种正交性导致前后各级之间的无耦性能(decoupleing property),这种性能十分有用,它使全局最优可以用各级局部最优来实现.当用作自适应滤波器时,各级可选择不同的自适应步长,使其收敛速度提高,而横向延时抽头滤波器不存在这种正交性质,因而也没有这种由于各级间的无耦性能带来的这些优点.
5.7.2 Burg递推算法——Kp的确定
Burg递推算法的优点是不需要估计自相关函数,可以直接从已知的x(n)序列求得参数Kp0另外,这种算法可保证满足稳定性的充要条件:.
如果Kp按前向均方误差最小的准则确定并用kep表示,则按式(5.106)
令
即
所以 (5.119)
如果Kp按后向均方误差最小的准则确定并用kbp表示,则按式(5.109)
即
所以 (5.120)
Burg算法是以前向均方误差与后向均方误差之和最小为准则求得Kp0令
即
所以 (5.121)
对于平稳随机过程,集合平均可用时间平均代替,因此上式可写成:
(5.122)
由式(5.114),(5.115),(5.116)不难看出
(5.123)
如果已知x(n)为有限长序列x0,x1,…,xN-1,(即x(0),x(1),…,x(N-1)),当p=1时,则按式(5.122)可得
(5.124)
而按式(5.106)及(5.109)可得
(5.125)
(5.126)
将e1(n)及b1(n)代入式(5.122),又可得
(5.127)
再代入式(5.106)及(1.109)又可得e2(n)及b2(n):
这里 (见式(5.105))
再将e2(n)与b2(n)代入式(5.122)又可求得K3,将K3与e2(n)及b2(n)代入式(5.106)与(5.109)又可求得e3(n)与b3(n)…以此类推,可直接从时间序列x(n)求得各阶的Kp以及前向与后向误差ep(n)与bp(n).将各Kp(=app)代入式(5.105)又可求得各apk.于是将这些求得的AR系数代入式(5.59)(其中)即可求得功率谱的估计值.
注意,为了使式(5.122)求和的x(n)值不超出已知的N个x(n)(x0,x1,…,xN-1)的范围,在p=1时求和的上下限应为n=1到N-1(见式(5.124)),在p=2时求和的上下限应从n=2开始到N-1(见式(5.127)),p阶时的n应取
(5.128)
Burg递推算法,对于短的时间序列x(n)仍能得到较正确的估计,因此得到普遍应用.但Burg算法受Levinson关系式(5.105)的约束,(仍应用了自相关矩阵的Toeplitz性质,实际上只有开始无终的平稳随机序列才有这种性质),因此不能完全克服Levinson算法中的缺点,仍存在某些谱线分裂与频率偏移现象.
5.7.3 正反向线性预测最小二乘法
为了克服Burg算法的上述缺点,Clayton,Ulrych和Nuttall于1976年分别提出了按最小二乘方准则的正反向预测算法.这种方法对所有apk都按最小求得,从而消除了Burg算法中受Levinson关系式(5.105)的约束.用这种方法得到的谱估计在谱线分裂与频率偏移方面较Burg递推法有较大的改善.
如果前向和后向预测误差能量之和用表示,即
(5.129)
令
即
(5.130)
令
(5.131)
中的第一项是由前向产生的,第二项是由后向产生的.将式(5.131)代入式(5.130)得
(5.132)
按式(5.129)
将式(5.130)代入上式,使上式第二项为零,得
(5.133)
将式(5.133)与式(5.132)合拼写成矩阵形式,得
(5.134)
式(5.134)左边的矩阵(方阵)与式(5.93)左边的自相关矩阵不同,它不是Toeplitz矩阵,同时矩阵中的各元素均有二个变量,按式(5.131)是与时间n有关的,因此这种方法也适用于非平稳的信号,它不要求信号x(n)是无始无终的平稳序列.这个矩阵常称为自协方差矩阵.此名字来自语音信号处理文献中的习惯称法,它与我们在第一章中从统计观点讨论的自协方差函数并不是一回事.利用式(5.134)求各系数apk(k=1, 2, …, p),从而求得功率谱估计的方法,虽然有前面讨论到的优点,但它不能保证各,因而不能保证滤波器的稳定性,另一方面它所需的计算工作量大.S.L.Marple[20]对这种方法提出了一种新的递推算法,可减少计算工作量.
近年来还出现很多其它提高分辨率的方法(见§5.1),即于篇幅,这里不再一一讨论,有兴趣的读者清查看有关参考文献[1][2].
参考文献
(1) S. M. Kay and S. L. Marple, "Spectrum Analysis——A Modern perspective", Proc. IEEE, Vol.69 No. 11, Nov, 1981pp.1380-1419
(2) A. V. Oppenheim & R. W. Schafer, "Digital Signal Processing", Prentice-Hall, Englewood Cliffs, N.J.1975
(3) S. A. Tretter, "Introduction to Discrete-Time Signal Processing", John Wiley & Sons, 1976
(4) J. Makhoul, "Linear Prediction: A Tutorial Review", Proc. IEEE, Vol. 63, No. 4, April 1975, pp. 561-580
(5) J. P. Burg, "Maximum Entropy Spectral Analysis", Proc. of the 37th Meeting of the Society of Exploration Geophysicists 1967. "Modern Spectrum Analysis", D. G. childers Ed, New Yok IEEE Press, 1978, pp34-41
(6) R. E. Dubroff, "The Effective Autocorrelation function of Maximum Entropy Spectra", Proc. IEEE, Vol. 63, Nov. 1975, pp.1622-1623
(7) J. A. Edward and M. M. Fitelson, "Notes on Maximum Entropy Processing", IEEE Trans, Inform. Theorg, Vol IT-19 pp. 232-234, Mar.1973
(8) A. Pappulis, "Maximum Entropy and Spectral Estimation: A Review", IEEE Trans, Assp-29, No.6, Dec.1981, pp 1176-1186
(9) J. Makhoul, "Stable and Efficient Lattice Methods for Linear Prediction", IEEE Trans. ASSP-25, Oct.1977, pp423-428
(10) J. Makhoul, "A class of all-zero Lattice Digital Filters: Properties and Application", IEEE Trans. ASSP-26. pp. 304-314, Aug. 1978
(11) J. P. Burg, "A New Analysis Technique for time Series Data", Presented at the NATO Advanced Study Institute on Signal Processing with Emphasis on underwater Accoustics, Aug 1969. "Modern Spectrum Analysis", D. G. Childers Ed New York IEEE Press, 1978, pp. 42-48
(12) B. Friedlander, "Lattice Filters for Adaptive Processing" Proc. IEEE. Sept, 1982
(13) 王宏禹:"最大熵谱分析"通讯学报,Vol.3,No.1,1982
(14) 王宏禹:"信号处理中提高谱估计分辨率的方法",通讯学报,1983年4月,第4卷,第2期
(15) M. L. Honig & D. G. Messerschmitt, "Convergence Properties of an Adaptive Digital Lattice Filter" IEEE Trans. ASSP-29, No.3 June 1981
(16) D. N. Swingier, "A modified Burg Algorithm for Maximum Entropy Spectral Aralysis", Proc. IEEE, Vol.67, pp 1368-1369, Sept. 1979
(17) D. N. Swingier, "Comments on Maximum Entropy Spectral Estimation using the Analytical Signal", IEEE Trans. Assp-28, pp. 259-260, Apr.1980
(18) A. S. Silisky, "Relationship between Digital signal precessing and control and Estimation Theory", Proc. IEEE, Vol. 66, pp. 996-1017,Sept, 1978
(19) M. L. Honig & D. G. Messerschmitt, "Convergence Models for Adaptive Gradient and Least square Algorithms", Proc, 1981 IC ASSP
(20) S. L. Marple, "A New Autoregressive Spectrum Analysis Algorithm", IEEE Trans, ASSP-28, No.4, Aug, 1980, pp. 441-454
(21) T. J. Ulrych and T. N. Bishop, "Maximum Entropy Spectral Analysis and Autoregressive Decomposition" Rev. Geophys. Space physice, vol.13, Feb.1975, pp183-200
(22) D. E. Smylie, G. K. C. Clarke, T. J. Ulrych, "Analysis of irregularities in the earth's Rotation" in Methods in Computational physics, vol.13. B. A. Bolt, Ed, New York: Academic press, 1973 pp.391-430
(23) C. K. Yuen, "A Comparison of five Methods for computing the power Spectrum of a random process Using Data Segmentation", Proc. IEEE, vol.65, pp.984-986, June 1977
(24) C. K. Yuen, "Comments on Modern Methods for Spectral Estimation", IEEE Trans, Assp.27, pp. 298-299, June 1979
(25) "Programs for Digital Signal pro Cessing", Ddited by Digital Signal processing committee IEEE Acoustics, Speech, and Signal processing Society, IEEE press 1979
(26) B. Friedlander, "Lattice method for Spectral Estimation" Proc. IEEE vol. 70, No.9 Sept. 1982
(27) G. M. Jenkins and D. G. Watts, "Spectral Analysis and its Applications", San Francisco, CA, Holden-Day, 1968
(28) 复旦大学编:"概率论"人民教育出版社,1981年
(29) P. D. Welch, "The Use of Fast Fourier Transform for the Estimation of Power Spectra: A method Based on Time Averaging over Short, Modified Periodograms", IEEE Trans. Audio and Electroacoust, Vol. AU-15, June 1997
功率的定义
文件类型:PPT/Microsoft Powerpoint 文件大小:字节
更多搜索:功率定义B 功率
一,功率的定义
功与完成这些功所需的时间之比.(单位时间所作的功)
物理意义:描述做功快慢的物理量.
表达式:P=W/t
单位:瓦特(W) 1W=1J/s
另一表达式:P=Fv
瞬时功率和平均功率
额定功率和实际功率
二,公式的应用
F一定时,P与v成正比
当F一定时,随着v的增大,P增大,当功率P达到最大功率时,加速运动结束, vt=P/F
P一定时,F与v成反比
当P一定时,通过减小牵引
力以增加速度,当F=f时,
vm=P/F=P/f
O
t
V
Vmax
示例1
重2t的汽车由静止起匀加速向山上开去,山的坡度为0.02,开出100m后,汽车速度增加到32.4km/h,若摩擦阻力是车重的0.05倍,求:
(1)发动机的牵引力;
(2)开出100m时汽车的功率;
(3)发动机所做的功;
(4)汽车克服摩擦阻力所做的功;
(5)汽车的平均功率.
(1)2210N
(2)19890W
(3)221000J
(4)100000J
(5)9945W
示例2
一个质量为m的物体,在几个与水平面平行的力作用下静止在光滑水平面上,在t=0时刻,将其中的一个力从F增加到3F,其他力保持不变,则在t=t1时刻,该力做功的功率为( )
A.9F2t1/m; B.6F2t1/m;
C.4F2t1/m; D.3F2t1/m.
B
示例3
一辆汽车沿一略微倾斜的坡路运动,若保持发动机的功率不变,它能以速度v1匀速上坡,能以速度v2匀速下坡,则当它在相同材料的水平路面上行驶时,能达到的最大速度为(设汽车在坡路和水平路面上行驶时所受阻力相同)
A,v1 v2 B,(v1 + v2)/2
C,2v1 v2/(v1 + v2)D, v1 v2/(v1 + v2)
C
示例4
一辆卡车质量为4T,其发动机额定功率为60kW,当它在坡度为0.05的斜坡上行驶时,所受阻力为车重的0.1倍.求:
①卡车上坡时所能达到的最大速度;
②若卡车从静止开始以加速度0.5m/s2作匀加速运动上坡,则这一过程能维持多长时间
10,15
http://rywen.net/view/48905
!!!参数模型功率谱估计
http://www.docin.com/p-619769.html
一类双线性时间序列模型基于累积量的辨识*
余 勇 万德钧
摘 要 获得了一类双线性时间序列模型的二、三和四阶累积量所满足的差分方程,它们与线性平稳ARMA模型著名的Yule-Walker方程相似,可看作是标准Yule-Walker方程的推广.因此它们可用于双线性时间序列模型的辨识,并以一个数值仿真例子表明该方法是可行的.
直接用矩阵求逆解Yule-Walker方程运算量较大,Levinson-...
还有估计AR模型参数的Yule-Walker方程法、基于线性预测理论的Burg算法
厦门大学计算机科学系
Scilab Speech语音识别
http://scispeech.sourceforge.net/Chinese/Dev-ana.htm
时域分析
频域分析
倒谱分析
WRLS-VFF分析
时域分析
语音信号的时域分析就是分析和提取语音信号的时域参数。进行语音分析时,最先接触到并且也是最直观的是它的时域波形。语音信号本身就是时域信号,因而时域分析是最早使用,也是应用最广泛的一种分析方法,这种方法直接利用语音信号的时域波形。时域分析通常用与最基本的参数分析及应用,如语音的分割,预处理等。这种分析方法的特点是:①表示语音信号比较直观、物理意义明确。②实现其起来比较简单、预算量少。③可以得到语音的一些重要的参数。④只使用示波器等通用设备,使用较为简单等。
语音信号的时域参数有短时能量、短时过零率、短时自相关函数等,这是语音信号的一组最基本的短时参数,在各种语音信号数字处理技术中都有应用。
短时能量分析:
设语音波形时域信号为x(l),分帧加窗处理后得到的第n帧语音信号为 ,则 满足下式:
其中,n=0,1T,2T,...,并且N为帧长,T为帧移长度。
设第n帧语音信号 的短时能量用 表示,则其计算公式如下:
是一个度量语音信号幅度值变化的函数。
短时过零率分析:
短时过零率表示一帧语音中语音信号波形穿过横轴(零电平)的次数。过零分析是语音时域分析中最简单的一种。对于连续语音信号,过零即以为着时域波形通过时间轴;而对于离散信号,如果相邻的取样值改变符号则成为过零。过零率就是样本改变符号的次数。
定义语音信号 的短时过零率 为:
式中,sgn[]是符号函数,即:
短时自相关函数:
相关分析是一种常用的时域波形分析方法,对于确定性离散信号[x(n)],能量有限,其子相关函数定义为: (2.1.1)
如果{x(n)}是随即或者周期性的离散信号,不是能量有限的,那么其自相关函数的定义为:
由自相关函数的定义可以看出其所具有的一些性质:(1)自相关函数是偶函数,满足R(k)=R(-k); (2)k=0时函数取得最大值,此时,对于确定性信号,自相关函数的取值就是该信号的能量,对于随即信号或者周期信号,自相关函数的取值是该信号的平均功率;(3)如果原序列是周期为T的周期信号,那么自相关函数也是周期为T的周期函数,即R(k)=R(T+k)。
短时自相关函数的定义为:
上式的物理意义为:首先用窗函数选择要处理的语音,然后将窗选结果带入(2.1)式得到上式。利用自相关函数是偶函数的性质,有
如果定义 ,上式变形为:
即为序列[x(n)x(n-k)]通过单位冲激响应为 的滤波器后的输出。
back to top
频域分析
语音信号的频域分析就是分析语音信号的频域特征。从广义上讲,语音信号的频域分析包括语音信号的频谱,功率谱,倒频谱等,这里实现了语音信号的线性预测法。线性预测是一种很重要的技术,几乎普遍地应用与语音信号处理的各个方面。
线性预测分析的基本思想是:由于语音样点之间存在相关性,所以可以用过去的样点值来预测现在或未来的样点值,即一个语音的抽样能够用过去若干个语音抽样或它们的线性组合来逼近。通过使实际语音抽样和线性预测抽样之间的误差在某个准则下达到最小值来决定唯一的一组预测系数。而这组预测系数就反映了语音信号的特征,可以作为语音信号特征参数用与语音识别、语音合成等。
将线性预测应用与语音信号处理,不仅是因为它的预测功能,而且更重要的是因为它能提供一个非常好的声道模型及模型参数估计方法。线性预测的基本原理和语音信号数字模型密切相关。
用线性预测误差滤波器来实现,线性预测误差滤波器的传递函数为:
其中p为预测器阶数, 为线性预测器系数。
线性预测模型为:
,其中, 称为s(n)的预测值。线性预测分析(LPA)实质上就是设计一个预测误差滤波器A(z),即求解 使得预测误差e(n)在某个预定的准则下最小。理论上通常采用均方误差 最小准则。根据e(n)的定义, 的数学期望为:
令 ,即
将e(n)代入得
其中 是s(n)的自相关序列。
公式 可写成(Yule-Walker方程):r-RA=0
r:自相关矢量
R:自相关矩阵
A:预测系数矢量
自相关矢量、自相关矩阵和预测系数矢量的矩阵表示为:
协方差法:
协方差法的定义为 ,其中s(n)的长度范围为: 。s(n)的协方差定义为: 。
由 可得 ,
即:
由上面可以看出协方差的特点有:
①不需要加窗,计算精度高
②不满足 ,即不能保证系统的稳定性,进行线性预测分析时,不得不随时判定H(z)的极点位置,不断加以修正,才能得到稳定的结果
伯格法:
伯格法的基本思想是使正向和反向预测误差的平方和最小,即
。 令 ,则
,由Schwarz不等式可以证明: 。
Burg法能保证合成滤波器的稳定。
RMLE:
这里将要描述另一种估计模型参数的方法。RMLE(recursive maximum likelihood estimator),是一种接近于MLE但是采用线性预测的方法,它采用的是递归的方式。
感知线性预测法:
感知线性预测(PLP)分析法基于许多听觉的心理学概念。它的整个流程块图如下:
语谱分析:
最常用的语谱分析是periodogram,它的定义如下:
其中X(n)是一个任意的序列.
back to top
倒谱分析
语音信号的倒谱分析就是求取语音倒谱特征参数的过程,它可以通过同态处理来实现。同态信号处理也成为同态滤波,它实现了将卷积关系变换为求和关系的分离处理,即解卷。对语音信号进行解卷,可将语音信号的声门激励信息及声道响应信息分离开来,从而求得声道共振特性和基音周期,用与语音编码、合成、识别等。对语音信号进行解卷,求取倒谱特征参数的方法有两种:一是线性预测分析,一是同态分析处理。这里我们讨论通过同态处理的倒谱分析方法。
如图2.3a所示为一卷积同态系统的模型,该系统的输入卷积信号经过系统变换后输出的是一个处理过的卷积信号。这种同态系统可分解为三个子系统,如图2.3b所示,即两个特征子系统和一个线性子系统。第一个子系统(如图2.3c),它完成将卷积性信号转化为加性信号的运算;第二个子系统是一个普通线性系统,满足线性叠加原理,用于对加性信号进行线性变换;第三个子系统是第一个子系统的逆变换,它将加性信号反变换为卷积信号,如图2.3d所示。在图2.3中,符号*、+和.分别表示卷积、加法和乘法。
back to top
WRLS-VFF分析
若要做WRLS-VFF分析,首先我们要先引进一个假设:所有的语音信号都是用以下的模型产生的。
并引入两个定义,一个为参数矢量,一个为数据矢量。如下等式所示:
通过以上所引入的一个假设,两个定义,我们可以定义一个完整且稳定的带输入估计的WRLS-VFF算法,其核心定义如下:
Prediction error:
Gain update:
Forgetting factor:
Input estimate:
a)if λk<λ0 then
b)if λk>λ0 then
Parameter update:
Covariance matrix:
back to top
现代信号处理技术http://wenku.baidu.com/view/f4090d0203d8ce2f00662385.html
现代信号谱分析
(美)斯托伊卡译者:吴仁彪
电子工业出版社
出版时间: 2007年11月 ISBN: 9787121052422 开本: 16开 定价: 58.00 元
内容提要
本书译自国际著名信号处理大师、IEEE信号处理协会技术成就奖获得者PetreStoica教授2005年编写的教材《SpectralAnalysisofSignals》。该书介绍了经典谱分析和现代谱分析的基本理论和方法,主要内容包括谱估计的基本概念(自相关,能量谱和功率谱),非参数化谱分析(周期图和相关图,加窗技术),有理谱分析(自回归,滑动平均以及自回归滑动平均方法),线谱分析(最小二乘估计,Yule-Walker和子空间方法),滤波器组方法(改进的滤波器组方法,Capon方法,APES方法),阵列信号处理(波束形成,Capon方法,参数化波达方向估计),有关矩阵分析、Cramer-Rao理论和模型阶数选取的主要结论。书中每章包含了大量反映谱分析最新研究成果和当前研究热点的补充内容,提供了大量有助于读者深入了解各种谱分析方法性能与实现、反映当前研究热点的分析习题和上机习题。该书内容丰富新颖、论述严谨,是一本信号谱分析领域的高水平教材。
作者简介
吴仁彪,1966年2月生于武汉市。1991年在西北工业大学首届教改试点班(五年半本硕连读)毕业,1994年在西安电子科技大学获博士学位。先后四次以博士后、访问教授、国家首批高级研究学者的身份在美国佛罗里达大学和英国帝国理工大学工作近五年。现任中国民航大学智能信号与图像处理天津市重点实验室主任,天津市首批三位特聘教授之一,中国民航总局首批特聘专家,天津大学和西安电子科技大学博士生导师,IEEE高级会员,中国电子学会理事和学术工作委员会委员。研究方向为自适应信号处理、阵列信号处理和现代谱估计及其在雷达、导航、通信中的应用。共发表学术论文150余篇,其中50余篇发表在IEEE和IEE会刊上,被SOI,EI和ISTP收录100余篇。曾获省部级科技成果奖励7项,国家发明专利6项。1999年入选国家人事部百千万人才工程第一、二层次培养对象,2005年荣获国家杰出青年基金。
目录
第1章 基本概念 第2章 非参数化方法 第3章 有理谱估计的参数化方法 第4章 线谱估计的参数化方法 第5章 滤波器组方法 第6章 空域方法 附录 参考文献
 爱华网
爱华网