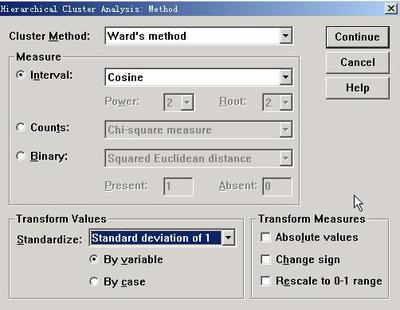
y=dsolve(f1,f2,...,fmO; y=dsolve(f1,f2,...,fm,'x'); |
| syms t; u=exp(-5*t)*cos(2*t-1)+5; uu=5*diff(u,t,2)+4*diff(u,t)+2*u; syms t y; y=dsolve(['D4y+10*D3y+35*D2y+50*Dy+24*y=87*exp(-5*t)*cos(2*t-1)+92*exp(-5*t)*sin(2*t-1)+10'])yc=latex(y) |
将yc的内容copy到latex中编译,得到结果。
关于Matlab的微分方程,直到今天才更新第2篇,实在是很惭愧的事——因为原因都在于太懒惰,而不是其他的什么。
在上一篇中,我们使用dsolve可以解决一部分能够解析求解的微分方程、微分方程组,但是对于大多数微分方程(组)而言不能得到解析解,这时数值求解也就是没有办法的办法了,好在数值解也有很多的用处。
数值分析方法中讲解了一些Eular法、 Runge-Kutta法等一些方法,在matlab中内置的ode求解器可以实现不同求解方法的相同格式的调用,而不必太关心matlab究竟是用什么算法完成的。
这一回我们来说明ode45求解器的使用方法。
1.ode45求解的上手例子:
求解方程组
Dx=y+x(1-x^2-y^2);
Dy=-x+y*(1-x^2-y^2)
初值x=0.1;y=0.2;
先说明一下最常用的ode45调用方式,和相应的函数文件定义格式。
[t,x]=ode45(odefun,tspan,x0);
其中,Fun就是导函数,tspan为求解的时间区间(或时间序列,如果采用时间序列,则必须单调),x0为初值。
这时,函数文件可以采用如下方式定义
function dx=odefun(t,x)
对于上面的小例子,可以用如下的程序求解。
function jixianhuan function dx=jxhdot(t,x) |
2.终值问题
tspan可以是递增序列,也可以为递减序列,若为递减则可求解终值问题。
[t,x]=ode45(@zhongzhiode,[3,0],[1;0;2]);plot(t,x)
function dx=zhongzhiode(t,x)
dx=[2*x(2)^2-2;
-x(1)+2*x(2)*x(3)-1;
-2*x(2)+2*x(3)^2-4];
结果如下
3.odeset
options = odeset('name1',value1,'name2',value2,...)
[t,x]=solver(@fun,tspan,x0,options)
通过odeset设置options
第一,通过求解选项的设置可以改善求解精度,使得原本可能不收敛的问题收敛。
options=odeset('RelTol',1e-10);
第二,求解形如M(t,x)x'=f(t,x)的方程。
例如,方程
x'=-0.2x+yz+0.3xy
y'=2xy-5yz-2y^2
x+y+z-2=0
可以变形为
[10 0][x'] [-0.2x+yz+0.3xy]
[010][y']=[2xy-5yz-2y^2 ]
[00 1][z'][x+y+z-2]
这样就可以用如下的代码求解该方程
function mydae
M=[1 0 0;0 1 0;0 0 0];
options=odeset('Mass',M);
x0=[1.6,0.3,0.1];
[t,x]=ode15s(@daedot,[0,1.5],x0,options);plot(t,x)
function dx=daedot(t,x)
dx=[
-0.2*x(1)+x(2)*x(3)+0.3*x(1)*x(2);
2*x(1)*x(2)-5*x(2)*x(3)-2*x(2)*x(2);
x(1)+x(2)+x(3)-2];
4.带附加参数的ode45
有时我们需要研究微分方程组中的参数对于解的影响,这时采用带有参数的ode45求解会使求解、配合循环使用,可以使得求解的过程更加简捷。
使用方法:只需将附加参数放在options的后面就可以传递给odefun了。
看下面的例子。
function Rossler
clear;clc
a=[0.2,0.2];
b=[0.2,0.5];
c=[5.7,10];
x0=[0 0 0];
for jj=1:2
[t,x]=ode45(@myRossler,[0,100],x0,[],a(jj),b(jj),c(jj));
figure;plot3(x(:,1),x(:,2),x(:,3));grid on;
end
function dx=myRossler(t,x,a,b,c)
dx=[
-x(2)-x(3);
x(1)+a*x(2);
b+(x(1)-c)*x(3)];
5. 刚性方程的求解
刚性方程就是指各个自变量的变化率差异很大,会造成通常的求解方法失效。
这是matlab中自带的一个例子,使用ode15s求解,如果用ode45求解就会出现错误。
function myode15study
[t,Y] = ode15s(@vdp1000,[0 3000],[2 0]);
plot(T,Y(:,1),'-o')
figure;plot(Y(:,1),Y(:,2))
function dy = vdp1000(t,y)
dy =zeros(2,1);
dy(1) = y(2);
dy(2) = 1000*(1 - y(1)^2)*y(2) - y(1);
6.高阶微分方程的求解
通常的方法是进行变量替换,将原方程降阶,转换成更多变量的一阶方程组进行求解。
在这个例子里我们求解一个动力学系统里最常见的一个运动方程
,其中f=sin(t)
function myhighoder
clear;clc
x0=zeros(6,1);
[t,x]=ode45(@myhigh,[0,100],x0);
plot(t,x(:,1))
function dx=myhigh(t,x)
f=[sin(t);0;0];;
M=eye(3);
C=eye(3)*0.1;
K=eye(3)-0.5*diag(ones(2,1),1)-0.5*diag(ones(2,1),-1);
dx=[x(4:6);inv(M)*(f-C*x(4:6)-K*x(1:3))];
7.延迟微分方程
matlab提供了dde23求解非中性微分方程。dde23的调用格式如下:
sol = dde23(ddefun,lags,history,tspan)
lags是延迟量,比如方程中包含y1(t-0.2)和y2(t-0.3)则可以使用lags=[0.2,0.3]。
这里的ddefun必须采用如下的定义方式:
dydt = ddefun(t,y,Z)
其中的Z(:,1)就是y(t-lags(1)),Z(:,2)就是y(t-lags(2))...
下面是个使用dde23求解延迟微分方程的例子。
function mydde23study
%The differential equations
%
%y'_1(t) = y_1(t-1)![[转载]MATLAB解微分方程 matlab 微分方程组](http://img.aihuau.com/images/01111101/01061225t016d96c4c627953298.jpg)
%y'_2(t) = y_1(t-1)+y_2(t-0.2)
%y'_3(t) = y_2(t)
%
%are solved on [0, 5] with history y_1(t) = 1, y_2(t) = 1, y_3(t) =1 for
% t<= 0.
clear;clc
lags=[1,0.2];
history=[1;1;1];
tspan=[0,5];
sol = dde23(@myddefun,lags,history,tspan)
plot(sol.x,sol.y)
function dy = myddefun(t,y,Z)
dy=[
Z(1,1);
Z(1)+Z(2,2);
y(2)];
8.ode15i求解隐式微分方程
[T,Y] = ode15i(odefun,tspan,y0,yp0)
yp0为y'的初值。
odefun的格式如下 dy =odefun(t,y,yp),yp表示y',而方程中应该使得f(t,y,y')=0
function myodeIMP
%The problem is
%
%y(1)' = -0.04*y(1) + 1e4*y(2)*y(3)
%y(2)' = 0.04*y(1) - 1e4*y(2)*y(3) -3e7*y(2)^2
%y(3)' = 3e7*y(2)^2
%
%It is to be solved with initial conditions y(1) = 1, y(2) = 0, y(3)= 0
%to steady state.
clear;clc
y0=[1;0;0];
fixed_y0=[1;1;1];
yp0=[0 0 0];
fixed_yp0=[];
[y0mod,yp0mod]=decic(@myodefunimp,0,y0,fixed_y0,yp0,fixed_yp0);
tspan=[0, logspace(-6,6)];
[t,y] = ode15i(@myodefunimp,tspan,y0mod,yp0mod);
y(:,2)=1e4*y(:,2);
semilogx(t,y)
function res=myodefunimp(t,y,yp)
res=[
-yp(1)-0.04*y(1)+1e4*y(2)*y(3);
-yp(2)+0.04*y(1)-1e4*y(2)*y(3)-3e7*y(2)^2;
-yp(3)+3e7*y(2)^2;
];
这次要接触一个新的求解ode的方法,就是使用simulink的积分器求解。
1.还是做我们研究过的一个例子(在初识matlab微分方程(2)中采用的)。
Dx=y+x(1-x^2-y^2);
Dy=-x+y*(1-x^2-y^2)
初值x=0.1;y=0.2;
积分器中设置初始条件;f(u)中指定Dx,Dy的计算公式。
运行这个仿真,scope中可以看到两个变量的时程如下:
在WorkSpace里可以得到tout和yout,执行plot(yout(:,1),yout(:,1))得到与ode45求解相似的结果如下
2.这部分解决一个使用ode求解器dde23没法求解的一类延迟微分方程(中性微分方程)。
形如x'(t)=f(x'(t-t1),x(t),x(t-t2),x(t-t3))这类方程。dde23是无法求解的,但是可以借助simulink仿真求解。
看下面的这个例子。
x'(t)=A1*x(t-t1)+A2*x'(t-t2)+B*u(t)
t1=0.15;t2=0.5
A1=[-123-3]A2=[0.0200]B=[0]
[106-11662][00.030][1]
[207-207113][000.04][2]
在continuous里找到transport Delay,就可以实现对于信号的延迟,因此可以建立如下仿真模型
从而在scope中可以得到如下仿真结果
OK~初识微分方程到了这里我想应该可以做个终结,因为我想作为零基础的材料来看,到这里也就可以了。以后还可能再有微分方程的内容,还请感兴趣的朋友多捧场吧。
最后,大力推荐一本书薛定宇老师的《高等应用数学问题的Matlab求解》,确实很经典。学习Matlab的时间也不算短了,可是每次翻看这本书总是能让我有温故而知新的感觉,是我目前见过的最好的Matlab书。强烈推荐!(对于从来没有接触过matlab的人来说或许有点儿难,但是如果你以后要用matlab的话买一本绝对不会后悔的。)
[ 爱华网
爱华网