函数的值域问题及解法
函数y=f(x)的值域是函数值的取值范围,用集合表示为{y│y=f(x),x∈A}.
这里集合A是函数的定义域.由此可见,它与定义域密切相关.
值域的几何意义是函数图象上点的纵坐标的集合,也可以说成是函数图象纵向的分布范围.
一般来说,求值域比求定义域困难得多。求值域要根据解析式的结构特征选择适当的方法,具有较强的灵活性和一定的技巧性。
1.观察法
通过对函数定义域、性质的观察,结合函数的解析式,求得函数的值域。用于简单的解析式。
y=1-√x≤1,值域(-∞,1]本题通过直接观察算术平方根的性质而获解,这种方法对于一类函数的值域的求法,简捷明了,不失为一种巧法。
2.配方法
当所给函数是二次函数或可化为二次函数的复合函数时,可以利用配方法求函数值域。
例3:求函数y=x^2-4x+3的值域。 点拨:配方成完全平方式,利用二次函数的最值求。
点评:求函数的值域不但要重视对应关系的应用,而且要特别注意定义域对值域的制约作用。配方法是数学的一种重要的思想方法。
3. 换元法
以新变量代替函数式中的某些量,使函数转化为以新变量为自变量的函数形式,进而求出值域。
例2求函数y=x-3+√2x+1 的值域。
点拨:通过换元将原函数转化为某个变量的二次函数,利用二次函数的最值,确定原函数的值域。
解:设t=√2x+1 (t≥0),则
x=1/2(t^2-1)。
于是y=1/2×(t^2-1)-3+t=1/2×(t+1)^2-4≥1/2-4=-7/2.
所以,原函数的值域为{y|y≥-7/2}。
点评:将无理函数或二次型的函数转化为二次函数,通过求出二次函数的最值,从而确定出原函数的值域。这种解题的方法体现换元、化归的思想方法。它的应用十分广泛。
4.不等式法
用不等式的基本性质,也是求值域的常用方法。
y=(e^x+1)/(e^x-1), (0<x<1).
∵0<x<1,
∴1<e^x<e,0<e^x-1<e-1,
1/(e^x-1)>1/(e-1),
y=1+2/(e^x-1)>1+2/(e-1).值域(1+2/(e-1),+∞).
5.最值法
如果函数f(x)存在最大值M和最小值m.那么值域为[m,M].
因此,求值域的方法与求最值的方法是相通的.
6. 反函数法
函数和它的反函数的定义域与值域互换.
当函数的反函数存在时,则其反函数的定义域就是原函数的值域。
例2求函数y=(x+1)/(x+2)的值域。
点拨:先求出原函数的反函数,再求出其定义域。
解:显然函数y=(x+1)/(x+2)的反函数为:x=(1-2y)/(y-1),其定义域为y≠1的实数,故函数y的值域为{y�y≠1,y∈R}。
点评:利用反函数法求原函数的定义域的前提条件是原函数存在反函数。这种方法体现逆向思维的思想,是数学解题的重要方法之一。
7.单调性法
若f(x)在定义域[a, b]上是增函数,则值域为[f(a), f(b)].减函数则值域为[f(b), f(a)].
y=x^2-4x+3,(-1≤x≤1).
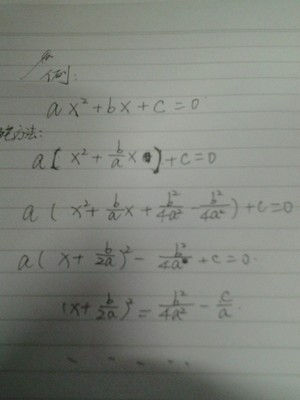
y=(x-2)^2-1在[-1, 1]上是减函数,
F(-1)=8,f(1)=0, 值域[0,8].点评:利用单调性求函数的值域,是在函数给定的区间上,或求出函数隐含的区间,结合函数的增减性,求出其函数在区间端点的函数值,进而可确定函数的值域。
8.分离常数法
点拨:将原分式函数,利用长除法转化为一个整式与一个分式之和。y=(1+x)/(1-x)=2/(1-x)-1
≠-1,值域(-∞,-1)∪(-1,+∞).9.判别式法
若可化为关于某变量的二次方程的分式函数或无理函数,可用判别式法求函数的值域。
例4求函数y=(2x^2-2x+3)/(x^2-x+1)的值域。
点拨:将原函数转化为自变量的二次方程,应用二次方程根的判别式,从而确定出原函数的值域。
解:将上式化为(y-2)x^2-(y-2)x+(y-3)=0 (*)
当y≠2时,由Δ=(y-2)^2-4(y-2)(y-3)≥0,解得:2<y≤10/3 当y=2时,方程(*)无解。∴函数的值域为2<y≤10/3。
点评:把函数关系化为二次方程F(x,y)=0,由于方程有实数解,故其判别式为非负数,可求得函数的值域。常适应于形如y=(ax^2+bx+c)/(dx^2+ex+f)及y=ax+b±√(cx^2+dx+e)的函数。
10.图象法
通过观察函数的图象,运用数形结合的方法得到函数的值域。
例6求函数y=�x+1�+√(x-2)2 的值域。
点拨:根据绝对值的意义,去掉符号后转化为分段函数,作出其图象。
解:原函数化为
{-2x+1(x≤-1)
y={3(-1<x≤2)
{2x-1(x>2)
它的图象如图所示。
显然函数值y≥3,所以,函数值域[3,+∞]。
点评:分段函数应注意函数的端点。利用函数的图象
求函数的值域,体现数形结合的思想。是解决问题的重要方法。
点评:对于形如y=(ax+b)/(cx+d)的形式的函数均可利用这种方法。路漫漫其修远兮吾将上下而求索求值域方法学法指导求值域方法 爱华网
爱华网