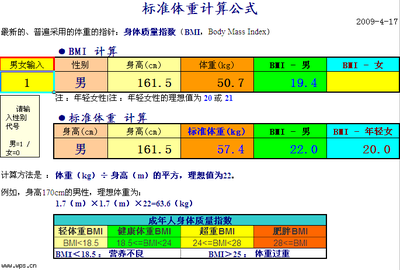
Birch算法全称是利用层次方法的平衡迭代约减和聚类(Balanced Iterative Reducing andClustering UsingHierarchis)。该算法的优点是:第一,只需要一次访问数据库,速度快。第二,相似数据在很大程度上得到压缩,节省了存储空间。第三,不需要大量递归运算。一个聚类有了这三个优点,不优秀都难了。它是Wisconsin-Madison大学Tian Zhang博士于1996年提出的聚类算法,采用B-树的思想实现(有点遗憾,要是这个算法也是韩佳炜老师发明的就好啦)。
Birch算法虽然采用B-树实现但是它又不是一个完全的B-树,因为第一,它的所有元素全部保存在叶子节点中,第二,在一个BTNode中的关键字间并没有大小关系,第三,当一个BTNode中的关键字个数大于指定数时,不需要将第(M+1)/2个关键字移到上一层节点中去,而是之间分裂成两个BTNode,再在上层中对应的BTNode中加个关键字。现在假定读者知道B-树的原理。先说明几个结构体:
//维信息,相同值会合并起来
//要按data排序,方便后面计算距离
typedef struct AttNode
{
//值
string data;
//具有该值的记录数目
unsigned int count;
//该维上下一个不同取值
AttNode *next;
}*AttTree;
//记录信息,也即是簇信息
typedef struct CFNode
{
//记录条数
unsigned int count;
//属性数组
//每个AttNode指针带头结点,方便合并两个CFNode
AttNode *atts[attNum];
}*CFTree;
//B-树
typedef struct BTNode
{
//已有CF数目
int keyNum;
//0号单元未用
//要是模仿B-树的话,应该是M+1,但是为了方便分裂就变成M+2了
//注意keys的第1位和ptr的0位对应,keys的第2位和ptr的1位对应,以此类推
CFTree keys[M+2];
BTNode *parent;
BTNode *ptr[M+2];
}*BTree;
//叶子结构体,用于将B-树的叶子节点连起来
typedef struct BLeafNode
{
BTree leaf;
BLeafNode *next;
}*BLeafTree;
//beginLeaft保存起始叶子节点的位置
BLeafTree beginLeaf;
以上各个结构体的注释已经很明确了,不需要再说明了,下面把这颗类B-树画出来:
图中一个BTNode最多包含4个CFNode,每个CFNode就相当于一个簇,而每个BTNode里面的所有CFNode相当于一个大簇。当插入一个新纪录时,是从底往上修改的,所以叶子节点是等深的,用BLeafNode将所有叶子节点窜连起来,方便挖掘这颗B-树。还是用例子说明吧。
先插入第一条记录,用该纪录创建一个CFNode,再用该CFNode创建一个BTNode作为根节点。图如下:
从第二条记录起就具有一般性了,插入第二条记录时,用该条记录创建一个临时CFNode,记cft,然后从根节点开始,看cft和根节点的哪个CFNode距离最近(当然目前只有一个CFNode),根据这个CFNode找到它的子BTNode(当然这里没有),一直这样下去,直到叶子节点(当然这里根节点也就是叶子节点)。假如cft和找到的最近的BTNode,记bt,的最近的那个CFNode,记cfp的距离是d,如果d小于给定的阈值minDis,则将cft和cfp合并,然后从该叶子节点向上跟新各个BTNode的信息直到跟节点,跟新的方法是将cft的信息合并到父节点的各个CFNode中(具体看代码吧)。如果d大于给定的阈值,但是bt的CFNode小于给定的阈值M,则将cft作为bt的一个新CFNode,然后依然从该叶子节点向上跟新各个BTNode的信息直到跟节点。如果bt的cfp大于给定的阈值M,则只能将bt分裂成两个BTNode,然后将原BTNode也就是bt所对应的父节点,记r,的对应的CFNode分裂成两个CFNode,如果那时r中的CFNode数目也大于M则继续向上分裂,否则向上跟新。这里有很多细节问题,也不好描叙,直接看代码吧。
下面讲下这么处理字符型数据。下面是以前做的笔记。
Birch算法也有不足的地方,第一,它对输入数据的先后顺序敏感,第二,每个CFNode将各条记录的数据相同的部分合并了,不能还原成原来的记录了。但是我们还是很方便求出每个簇的平均值等信息。
 爱华网
爱华网