这8个数据如果是样本,求方差应该用函数VARA( ),求得的结果是0.137;
求总体方差公式与求样本方差的公式差别是:求总体方差是除以n,求样本方差是除以(n-1)。
————————
顺便给你公式:附件:
之前一直对于样本方差与总体方差的概念区分不清,对于前者不仅多了“样本”两个字,而且公式中除数是N-1,而不是N。现在写下这么写东西,以能彻底把他们的区别搞清楚。
总体方差:
也叫做有偏估计,其实就是我们从初高中就学到的那个标准定义的方差,除数是N。如“果实现已知期望值,比如测水的沸点,那么测量10次,测量值和期望值之间是独立的(期望值不依测量值而改变,随你怎么折腾,温度计坏了也好,看反了也好,总之,期望值应该是100度),那么E『(X-期望)^2』,就有10个自由度。事实上,它等于(X-期望)的方差,减去(X-期望)的平方。”所以叫做有偏估计,测量结果偏于那个”已知的期望值“。
样本方差:
无偏估计、无偏方差(unbiasedvariance)。对于一组随机变量,从中随机抽取N个样本,这组样本的方差就是Xi^2平方和除以N-1。这可以推导出来的。 如果现在往水里撒把盐,水的沸点未知了,那我该怎么办?我只能以样本的平均值,来代替原先那个期望100度。同样的过程,但原先的(X-期望),被(X-均值)所代替。设想一下(Xi-均值)的方差,它不在等于Xi的方差,而是有一个协方差,因为均值中,有一项Xi/n是和Xi相关的,这就是那个"偏"的由来
证明: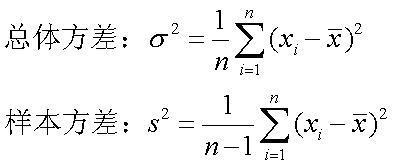
证毕~~
 爱华网
爱华网



