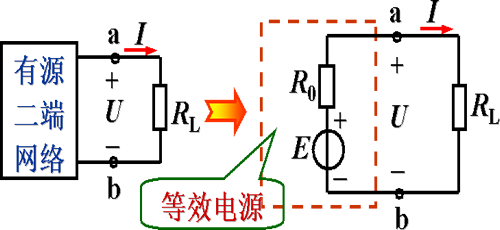
一定理
对于任一含源线性二端网络,就其两个端钮而言,都可以用一条最简单支路对外部等效。
1.以一条实际电压源支路对外部等效,其中电压源的电压值等于该含源线性二端网络端钮处开路时的开路电压,其串联电阻值等于该含源线性二端网络中所有独立源令为零时,由端钮处看进去的等效电阻,此即戴维南定理。
2.以一条实际电流源支路对外部进行等效,其中电流源的电流值等于该含源线性二端网络端钮处短接时的短路电流,其并联电阻的确定同1,此即诺顿定理。
这里。
上述定理可用图4-9和图4-10说明。
图4-9
图4-10
例1:求图4-11(a)所示电路的戴维南等效电路。
解:在图4-11(a)所示电路中求a、b两点的开路电压Uoc时,可以用前面介绍的支路法、网孔法、节点法、叠加法等方法进行,何种方法较为简便需考虑。显见若用叠加法进行时,仅涉及到常用的分压、分流关系即可,无需列写电路方程组解方程。
当1V电压源单独作用,如图4-11(b)利用分压公式。
(a)(b)
当1A电————流源单独作用,如图4-11(c)利用分流公式。
当1V电压源和1A电流源共同作用,如图4-11(a),由叠加法得
。
(c)
在图(a)所示电路中令独立源为零时,便成为图(d)的无源电阻网络。
(d)
∴图(a)的戴维南等效电路应为图(e)。
(e)
图4-11
结论:与理想电流源串联的元件对外部电路不起作用,可以短接。
例2:求图4-12(a)所示电路的戴维南等效电路。
图4-12(a)
分析:求戴维南等效电路的过程中,本身就可以采用戴维南定理,以使分析过程更加简捷。
解:本题可以将原电路分成左右两部分,先求出左面部分电路的戴维南等效电路,然后求出整个电路的戴维南等效电路。
左面部分电路的戴维南等效电路如图图4-12(b)
图4-12(b)
则原电路可等效图4-12(c)、(d)。
图4-12(c)图4-12(d)
[注意两点]
①与理想电压源并联的电阻对外部电路不起作用,可以断开。
②当两条相同的实际电压源支路并联时,其戴维南等效电路的准确求取。
二定理证明:
现设一个线性含源二端网络与一负载相联如图4-13(a)。当流过负载的电流为I时,则根据替代定理,可以用一个理想电流源替代该负载如图(b)。可见,此时,整个网络就成为一个线性网络。由此,可以利用叠加定理求a、b两点间的电压U。
将上述网络中的独立源分成两组,即线性含源二端网络中的所有独立源为一组,电流源I为一组。
当线性含源二端网络中的独立源共同作用时,电流源I断开,如图(c),此时求得的电压分量,即为a、b支路断开时的开路电压UOC,得。
当电流源I单独作用时,原线性含源二端网络中的所有独立源令为零值,如图(d),此时从a、b两点向左看即为等效电阻,则(注意参考方向)。
可见,由叠加定理即可得到a、b两点间的电压为:
由a、b两点间的伏安关系出发,可以构筑一个简单的等效电路,如图(e)。最后将理想电流源用负载替代如图(f)。
图(a)图(b)
| |||||||
图(c)图(d)
图(e)图(f)
图4-13
可见,在等效前后,a、b两点左端的网络对负载的影响总是不变的。而此时被等效的网络内部,其电压、电流的关系一般都是不等效的。
关于诺顿定理的证明可以采用相似的方法进行。
三求等效电阻的一般方法:
1.外加激励法
图4-14
2.开路短路法:
图4-15
,与的方向在断路与短路支路上关联
说明:求等效电阻时,若电路为纯电阻网络,可以用串、并联化简时,直接用串、并联化简的方法求,无法用串并联化简时,则用一般方法求。当电路中含受控源时,则一定要用一般方法求其戴维南等效电阻。
例3:电路如图4-16(a)所示,求无限扩展线性电阻网络,由任一支路看进去的等效电阻。
| |||||
(a)
(b)
(c)
图4-16
解:若求ab两点看进去的等效电阻Req,可以利用外加激励法,在a、b两点间加一个1A的电流源,设法求得其端电压U,则Req=。
采用电流源的分裂法,取无穷远为过渡点。利用叠加定理,由于无限扩展网络,当仅有一个电流源单独作用时,其电流均匀地向与a(b)点相联的四条支路分配,于是流过a、b间的电流为
则
可见,分析过程中使用了求等效电阻的一般方法、电流源的分裂方法及叠加定理三个知识点。
四.利用戴维南定理分析含受控源的电路
原则:1.被等效电路内部与负载内部不应有任何联系(控制量为端口U或I除外)
2.求要用一般方法
例4:电路如图4-17(a)所示,用戴维南定理求电压U。
(a)(b)
(c)(d)
(e)
图4-17
解:1.求,如图(b)所示。
∴
2.求,如图(c)所示。
则
或如图(d)所示,,
3.求电压U作出戴维南等效电路如图(e)所示。
例5:试求如图4-18(a)所示电路的等效电路。
解:对于较简单的含受控源的电路,若要求出它的戴维南等效电路,可以先直接写出电路端口上电压﹑电流的伏安关系,再由伏安关系去作等效电路。
(a)(b)
图4-18
由端口的伏安关系可以求得出Req=8,Uoc=0一步法(利用U-I关系)
则得等效电路如图4-18(b)所示。
五.最大功率传输
我们知道一个含源线性二端网络,总可以用一条戴维南等效电路对外部等效。当这个含源线性二端网络外接一个负载电阻时,如图4-19(a)所示,其中等效电源发出的功率将由等效电阻与负载电阻共同所吸收,如图4-19(b)所示。在电子技术中,总希望负载电阻上所获得的功率越大越好。那么,在什么条件下,负载电阻方可获得最大功率?负载电阻的最大功率值Pmax=?
(a)(b)
图4-19
我们知道:而
利用数学中求极值的方法:
令,得
即:当负载电阻RL与戴维南等效电阻Req相等时,负载电阻可从含源线性二端网络获得最大功率。此时最大功率为:
而戴维南等效电路中电源Uoc的效率
可见此时等效电源Uoc的效率只达50%,而Uoc所产生的功率有一半白白地损耗在等效电阻Req上,这在电力系统中是决不允许的,故电力系统中通常取RL>>Req。负载电阻吸收的功率和电源Uoc的效率随负载电阻变化的曲线如图4-20所示。
图4-20
注意:此时是指可调负载RL可获最大功率的条件为RL=Req,而不是Req可调。
 爱华网
爱华网