斯特瓦尔特(stewart)定理 设已知△ABC及其底边上B、C两点间的一点D,则有 AB^2·DC+AC^2·BD-AD^2·BC=BC·DC·BD。斯特瓦尔特定理的证明
证明:在图2-6中,作AH⊥BC于H。为了明确起见,设H和C在点D的同侧,那么由广勾股定理有 AC^2=AD^2+DC^2-2DC·DH,(1) AB^2=AD^2+BD^2+2BD·DH。 (2) 用BD乘(1)式两边得 AC^2·BD=AD^2·BD+DC^2·BD-2DC·DH·BD,① 用DC乘(2)式两边得 AB^2·DC=AD^2·DC+BD^2·DC+2BD·DH·DC。② 由 ① + ② 得到 AC^2·BD+AB^2·DC=AD^2(BD+DC)+DC^2·BD+BD^2·DC =AD^2·BC+BD·DC·BC。 ∴AB^2·DC+AC^2·BD-AD^2·BC=BC·DC·BD。 或者根据余弦定理得 AB^2=PB^2+PA^2-2PB·PA·cos∠APB AC^2=PA^2+PC^2-2PA·PC·cos∠APC 两边同时除以PB·PA·PC得 AC^2·PB+AB^2·PC=(PB^2+PA^2)PC+(PA^2+PA^2)PB 化简即可(注:图中2-7A点为P点,BDC点依次为ABC) 斯特瓦尔特定理的逆定理成立斯特瓦尔特定理的推论
斯特瓦尔特定理还有如下推论 (1)若AB=AC,则AP^2=AB^2-BP· PC (2)若AP为BC中线,则AP^2=1/2(AB^2+AC^2)-1/4*BC^2 (3)若AP为∠A内角平分线,则AP^2=AB·AC﹣BP·PC (4)若AP为∠A外角平分线,则AP^2=﹣AB·AC+BP·PC (5)若BP/BC=λ,则AP^2=λ·﹙λ﹣1﹚·BC^2+﹙1﹣λ﹚·AB^2+λ·AC^2 斯特瓦尔特定理与托勒密定理和张角定理可以互化斯特瓦尔特定理的常见应用方式
①用于得到线段倍份关系 ②用于求解三角形问题 (诀窍是选则适当的三角形及其边上的点;灵活运用推论)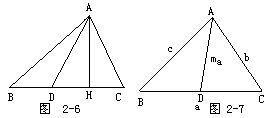
爱华网本文地址 » http://www.aihuau.com/a/25101014/234100.html
更多阅读

宿醉归来,五大节点!首先,法甲倒一布雷斯特还有两轮落后倒四埃维昂8分,意甲倒二锡耶纳与倒三巴勒莫还有一轮落后倒四热那亚7与5分,宣布赴继菲尔特、女王公园巡游者、雷丁、佩斯卡拉之后,贰零壹贰至贰零壹叁的五大联赛九十八或曰六大联赛幺

菲德尔·亚历杭德罗·卡斯特罗·鲁斯(Fidel Alejandro Castro Ruz,1926年8月13日-),古巴前国务委员会主席和部长会议主席,古巴共产党第一书记。2011年4月19日,古巴前领导人菲德尔·卡斯特罗在一份刊发的报纸中撰文证实,自己已经辞去古巴共产

从麦克里斯特尔的“折戟”说开去麦克里斯特尔,何许人也?堂堂美军驻阿最高指挥官,四星上将。曾因指挥参与活捉萨达姆、协助推翻塔利班政权而名噪一时。如此要职高官为何轻易“折戟”?说来理由也很简单:因其在最新一期《滚石》杂志的人物

没看过迈克尔杰克逊《危险布加勒斯特演唱会》,请不要说你喜欢流行乐、摇滚,请不要说你热爱杰克逊,请不要说你富有多么多么的激情………………因为这些都在迈克尔杰克逊罗马尼亚布加勒斯特站《危险之旅》演唱会。让喜欢周大帅、曾一棵和

敢死队2添加义项 这是一个多义词,请在下列义项中选择浏览1.2012年西尔维斯特·史泰龙主演电影2012年西尔维斯特·史泰龙主演电影2.策略类flash小游戏策略类flash小游戏3.动作射击类PC游戏动作射击类PC游戏1.2012年西尔维斯特·史泰龙主

 爱华网
爱华网



