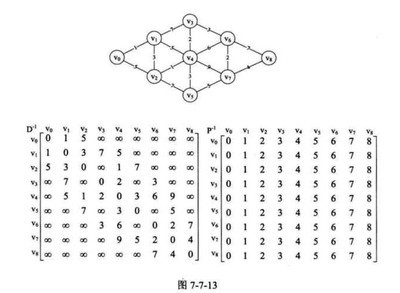
顶点对之间的最短路径是指:对于给定的有向网G=(V,E),要对G中任意一对顶点有序对V、W(V≠W),找出V到W的最短距离和W到V的最短距离。
解决此问题的一个有效方法是:轮流以每一个顶点为源点,重复执行迪杰斯特拉算法n次,即可求得每一对顶点之间的最短路径,总的时间复杂度为O(n3)。
弗洛伊德(Floyd)提出了另外一个求图中任意两顶点之间最短路径的算法,虽然其时间复杂度也是O(n3),但其算法的形式更简单,易于理解和编程。
算法基本思想:

弗洛伊德算法仍然使用图的邻接矩阵arcs[n+1][n+1]来存储带权有向图。算法的基本思想是:设置一个n x n的矩阵A(k),其中除对角线的元素都等于0外,其它元素a(k)[i][j]表示顶点i到顶点j的路径长度,K表示运算步骤。开始时,以任意两个顶点之间的有向边的权值作为路径长度,没有有向边时,路径长度为∞,当K=0时,A (0)[i][j]=arcs[i][j],以后逐步尝试在原路径中加入其它顶点作为中间顶点,如果增加中间顶点后,得到的路径比原来的路径长度减少了,则以此新路径代替原路径,修改矩阵元素。
#include<stdio.h>
#defineMAX 65535
voidFloyd()//若不需知道路径经过的点path[i][j],程序则不需要path[i][j]
{
intc[6][6]={{0,50,10,MAX,45,MAX},{MAX,0,15,MAX,10,MAX},{20,MAX,0,15,MAX,MAX},
{MAX,20,MAX,0,35,MAX},{MAX,MAX,MAX,30,0,MAX}, {MAX,MAX,MAX,3,MAX,0}};
intd[6][6],path[6][6];
intn=6;
inti,j,k;
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
d[i][j]=c[i][j];
if((i!=j)&&c[i][j]<MAX)
path[i][j]=i;
else path[i][j]=-1;
}
}
for(k=0;k<n;k++)
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{
if(d[i][k]+c[k][j]<d[i][j])
{
d[i][j]=d[i][k]+c[k][j];
path[i][j]=path[k][j];
}
}
printf("%d",d[0][1]);
printf("%d",d[0][4]);
printf("%d",d[2][4]);
}
int main()
{
Floyd();
return0;
}
 爱华网
爱华网