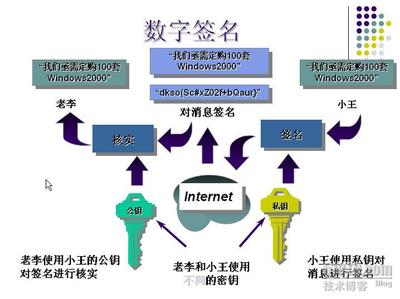
2.DSS,即DSA,当初的设计是用于数字签名而不用于密钥交换的算法,最初的设计是用来替换RSA的,是在ElGamal和Schorr数字签名方案的基础上设计的,这里不详细介绍这两个算法,有兴趣的同学可以自己去找找相关资料。与DH一样的密码数学基础,即素数域上中的模幂运算,最重要的区别构造p(大素数)时要使p-1可以被另一个称作q的素数除尽。与RSA不同的是,DSA签名结果是由两个值r和s(160位)组成。
算法原理:
1)参数介绍
p:L bits长的素数。L是64的倍数,范围是512到1024;
q:p - 1的160bits的素因子;
g:g = h^((p-1)/q) modp,h满足h < p - 1, h^((p-1)/q)mod p > 1;
x:x <q,x为私钥;
y:y = g^x mod p ,( p, q, g, y )为公钥;
以上参数中p, q, g以及y为公匙,x为私匙必须保密!任何第三方用户想要从Y解密成X 都必须解决整数有限域离散对数难题。
注:
a)、整数p, q,g 可以公开,也可仅由一组特定用户共享。
b)、私钥x 和 公钥 y 称为一个密钥对 (x,y) ,私钥只能由签名者本人独自持有,公钥则可以公开发布。密钥对可以在一段时间内持续使用。
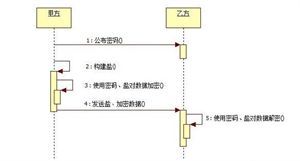
2)签名过程
P产生随机数k,k < q;
P计算r = ( g^k mod p ) modq
s = ( k^(-1) (H(m) + xr)) modq
签名结果是( m, r, s)。
注:
a)、k^(-1) 表示整数k关于某个模数的逆元,并非指k 的倒数。k在每次签名时都要重新生成。逆元:满足(a*b) mod m =1的a和b互为关于模数m 的逆元,表示为 a=b^(-1)或 b=a^(-1) ,如 (2*5) mod 3 = 1, 则 2 和 5 互为 模数3 的逆元。BTW:有兴趣实现的童鞋,可以参照GNUMP, 求k的模数逆元可以用GNU MP的mpz_invert函数.
b)、SHA(M):M的Hash值,M为待签署的明文或明文的Hash值。SHA是Oneway-Hash函数,DSS中选用SHA1( FIPS180: Secure Hash Algorithm),此时SHA(M) 为160bits长的数字串(16进制),可以参与数学计算(事实上SHA1函数生成的是字符串,因此必须把它转化为数字串)。
c)、最终的签名就是整数对( r , s ),它们和 M一起发送到验证方。
d)、尽管r 和 s 为 0 的概率相当小,但只要有任何一个为0, 必须重新生成 k,并重新计算 r和 s 。
3)验证过程
w =s^(-1)mod q
u1 = (H( m ) * w ) mod q
u2 = (r * w ) mod q
v = ((g^u1 * y^u2 ) mod p ) mod q
若v = r,则认为签名有效。
注:
a)、验证通过说明:签名( r, s )有效,即(r , s , M )确为发送方的真实签名结果,真实性可以高度信任,M 未被窜改,为有效信息。
b)、验证失败说明:签名( r , s )无效,即(r, s , M) 不可靠,或者M被窜改过,或者签名是伪造的,或者M的签名有误,M 为无效信息。
举个简单的例子:
参数选取:
1)取p=23,q=11是(p-1)=22的素因子。(p-1)/q=2(这两个数基本上是符合条件的比较小数字了,如果q取的太小,后面很多地方取值就体现不出来了))
2)g =h^((p-1)/q) mod p。取h=12,g=12^2 mod 23 =6<>1,满足条件,生成Zp*中唯一的q阶循环了群。
3)选择x=8,满足1<8<q
4)计算y= g^x mod p=6^8 mod 23 = 1679616 mod 23 = 18
所以公钥p=23,q=11,g=6,y=18
签名过程:
1)选择随机数k=7, 满足k<q
2)计算 r = ( g^k mod p ) mod q = (6^7 mod 23) mod 11 = 3 mod 11 =3
3)计算k^(-1) mod q=8
4)为了方便计算,随便取h(m)=10
5)s=k^(-1)(h(m)+xr) mod q =8*(10+8*3) mod 11 = 8
所以消息m的签名值r=3,s=8
验证过程:
1)计算w = (s^-1) mod q = 7
2)计算 u1 = (h(m)*w) mod q = 10*7 mod 11 = 4
3)计算 u2 = ( r * w ) mod q = 3*7 mod 11 = 10
4)计算v = (( g^u1 * y^u2 ) mod p ) mod q = ((6^4*18^10) mod23)mod11=3 mod 11 = 3
最后判断v是否与r相等,以决定是否通过了验证
证明公式:
因为:r=(g^k mod p) mod q;
s=(h(m)+xr)k^(-1) mod q;
w=s^(-1) mod q
u1 =(h(m)*w) mod q
u2 = (r * w ) mod q
v = ((g^u1 * y^u2 ) mod p ) mod q
所以:v = (( g^u1 * y^u2 ) mod p ) mod q
= ((g^(h(m)*w) * y^(r*w) mod p ) mod q
= ((g^(h(m)*w) * g^(x*r*w) mod p ) mod q mod p ) mod q
= ((g^((h(m)+(x*r)*w) mod p ) mod q mod p ) mod q
= ((g^(s*k*w) mod p ) mod q mod p ) mod q
= ((g^k mod p ) mod q mod p ) mod q
= r
所以,最后验证的时候只要v=r的时候,即可认为通过验证,这个推理等式用到了费尔马定理:
安全性分析:
DSA只能与SHA-1一起使用,而RSA可以与任何摘要算法一起使用。DSA签名不包括摘要标识符,所以如果允许多种摘要算法就会使DSA遭受前面RSA里面介绍的那种替换攻击。DSA主要依赖于整数有限域离散对数难题。素数P 必须足够大,且p-1至少包含一个大素数因子以抵抗Pohlig &Hellman算法的攻击。M一般都应采用信息的HASH值(官方推荐为SHA算法)。DSA的安全性主要依赖于p和g,若选取不当则签名容易伪造,应保证g对于p-1的大素数因子不可约。DSA算法在破解时关键的参数就是X 根据 Y = G^X mod P 只要知道 P,G,Y,Q 且能分解出 X 就可以伪造R,S写出KeyGen了。个人观点DSA的安全性要次于ECC 与RSA不相上下。但是有一点,就是DSA算法的验证过程R,S 是以明文形式出现的,这点很容易被利用。
BTW:与RSA不同的是,RSA是对签名数据“解密”后再比对摘要值,而DSA中摘要值是需要参与计算的。
 爱华网
爱华网