类就是把一组个体按照相似性原则归于若干类别,即“物以类聚”。其目的是使得属于同一类别的个体之间的距离尽可能小,而不同类别上的个体间的距离尽可能的大。聚类方法包括统计方法、机器学习方法、神经网络方法等。
在统计方法中,聚类又称为聚类分析,它是多元数据分析的三大方法之一,其它两种是回归分析和判别分析。它主要研究基于几何距离的聚类,如欧氏距离、明可夫斯基距离等,通过这些距离函数来进行聚类。
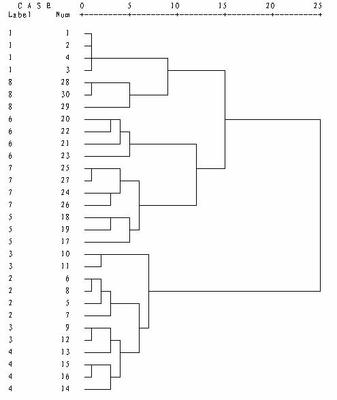
聚类分析就是根据某个特定的准则将样本集中相似的数据点目标点归为一类的一种数学方法,它是数理统计中多元分析的一个分支。聚类分析算法除了广泛应用于模式识别、图像分割、特征匹配等领域外,还在心理学、生理学、医学和地理学等领域中有广泛的应用。
聚类分析和判别分析有相似的作用,都是起到分类的作用。但是,判别分析是己知分类然后总结出判别规则,是一种有指导的学习而聚类分析则是有了一批样本,不知道它们的分类,甚至连分成几类也不知道,希望用某种方法把观测进行合理的分类,使得同一类的观测比较接近,不同类的观测相差较多,这是无指导的学习。所以,聚类分析依赖于对观测间的接近程度距离或相似程度的理解,定义不同的距离量度和相似性量度就可以产生不同的聚类结果。
综上所述:聚类分析的基本思想是将比较接近的样本归为一类。不过有可能预先并不知道分成几类,也可能预先已确定好分成几类。根据这两种不同的前提,聚类方法又大致分为系统聚类法,动态聚类法两类:
(1)系统聚类法:是一种基于模糊关系的分类法。其中包括基于模糊等价关系的聚类方法(传递闭包法)、基于模糊相似关系的聚类方法(直接法)、最大树方法(直接法)等等。
(2) 动态聚类法(迭代聚类法、ISODATA法)。
从集合论的观点看,聚类分析的实质是将作为论域的集合进行划分。
聚类分析的基本思想是用相似性尺度来衡量事物间的亲疏程度,并以此来实现分类,模糊聚类分析的实质就是根据研究对象本身的属性来构造模糊矩阵,在此基础上根据一定的隶属度来确定其分类关系。有关模糊聚类分析将在以后继续介绍。
 爱华网
爱华网