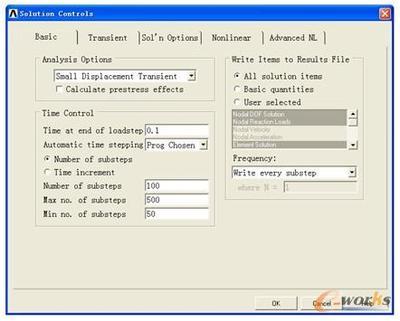
#转换数据框,不带“,”的数值型数据a<-as.data.frame(apply(zgtest,2,function(x){return(as.numeric(gsub(",","",x)))}))a$date<-as.factor(a$date)#date是因子
#给每一列标题改个名names(a)<-c("time","date","pv","uv","cupdown","c","cindex","cyesno","hsupdown","hs","hsindex","hsyesno")
#单因素方差分析library(multcomp)attach(a)table(date)#各组样本大小date1 2 34 512 12 11 12 12aggregate(pv,by=list(date),FUN=mean)#各组均值 Group.1 x1 1 4765.8332 2 5114.6673 3 5610.5454 4 5206.9175 5 5056.667aggregate(pv,by=list(date),FUN=sd)#各组标准差Group.1 x1 1 951.94622 2 973.56143 3 1387.04264 4 1462.83125 5 1493.8013fit<-aov(pv~date)#检验组间差异(ANOVA)summary(fit) Df Sum Sq Mean Sq F value Pr(>F)date 4 42597401064935 0.656 0.626Residuals 54 877176211624400
library(gplots)#绘制各组均值及其置信区间的图形plotmeans(pv~date,xlab="date",ylab="pv",main="mean plotnwith95% CI")
#均值显示date3的pv最多,而date1的pv最少;各组标准差存在差异,最低的date1951.9462,最高的date51493.8013;ANOVA对date的F检验不显著(P=0.562),说明组间pv无显著差异。
#对uv作组间差异检验(ANOVA)fituv<-aov(uv~date)summary(fituv) Df Sum Sq Mean Sq F valuePr(>F) date 4 11051657 2762914 3.279 0.0177 *Residuals 54 45505388842692 ---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#绘制各组均值及其置信区间的图形plotmeans(uv~date,xlab="date",ylab="uv",main="mean plotnwith95% CI")
#均值显示date1~date2的uv相似,而date5的uv突然减少;ANOVA对date的F检验显著(P=0.0177<0.05),说明组间uv有显著差异。
#多重比较multcomp包中glht()函数提供了多重均值比较更为全面的方法,即适用于线性模型,也适用于广义线性模型。#重现TukeyHSD的成对组间比较检验library(multcomp)par(mar=c(5,4,6,2))#增大顶部边界面积tukuv<-glht(fituv,linfct=mcp(date="Tukey"))plot(cld(tukuv,level=.05),col="lightgrey")#cld设置显著水平95%
#上图顶部有相同字母的组(用箱线图表示)说明均值差异不显著;date1、date2、date3、date4差异不显著,date4与date5差异不显著,date5与date1、date2、date3均有显著差异。
#评估检验的假设条件单因素方差分析中,假设因变量服从正态分布,各组方差相等。#用Q-Q图检验正态性假设library(car)qqPlot(lm(uv~date,data=a),simulate=T,main="Q-Qplot",labels=F)
#数据落在95%的置信区间范围内,说明满足正态性假设。
#方差齐性检验-Bartlett检验bartlett.test(uv~date,data=a)data: uv by dateBartlett's K-squared = 3.4486, df = 4, p-value =0.4857#Bartlett检验表明5组的方差没有显著不同(p-value= 0.4857)
#离群点检测library(car)outlierTest(fituv)No Studentized residuals with Bonferonni p <0.05Largest |rstudent|: rstudent unadjustedp-v alue Bonferonni p48 2.843038 0.0063331 0.37365#没有证据说明数据中含有离群点。根据Q-Q图、Bartleet检验和离群点检验,该数据用ANOVA模型拟合得很好。
 爱华网
爱华网