一、 t-分布
关于t 分布的早期理论工作,是英国统计学家威廉?西利?戈塞特(WillamSealy Gosset)在1900年进行的。
t分布是小样本分布,小样本分布一般是指n<30。t分布适用于当总体标准差R未知时用样本标准差s代替总体标准差R,由样本平均数推断总体平均数以及2个小样本之间差异的显著性检验等。
从平均值为L、方差为R2的正态总体中抽取容量为n的一个样本,其样本平均数 服从平均值为L,方差为R2/n的正态分布,因此,
。但是总体方差R2总是未知的,从而只能用s2来代替,
(1)如果n很大,那么,s2就是R2的一个较好的估计量,仍然是一个近似的标准正态分布;
(2)如果n较小, s2常常与R2的差异较大,因此,统计量就不再是一个标准正态分布,而是服从t分布。
(一)t分布的性质
1、t分布是对称分布,且其均值为0。
2、当样本容量n较小时,t分布的方差大于1; 当n增大到大于或等于30时,t分布的方差就趋近于1,t分布也就趋近于标准正态分布。
3、t分布是一个分布族,对于不同的样本容量都对应不同的分布,且其均值都为0。
4、与标准正态分布相比,t分布的中心部分较低,2个尾部较高。
5、变量t的取值范围在与之间。
t分布与标准正态分布的比较
(二)t分布的自由度
样本中独立观察值的个数(即样本容量)n减去1(由于样本要估计的总体参数的个数为1,即R2)。
如果用一个样本容量为n=20的样本估计总体平均数,那就要用14个自由度,以便选择适当的t分布。
(三) t分布表的使用
在使用t分布表时,必须同时具备置信度和自由度2个条件。
置信度表示被估计的总体参数落入置信区间的概率。然而,t分布给出的是A值,即表示所估计的总体参数不落入置信区间的概率,或落入置信区间以外的可能性。A的数值是由100%减去给定的置信度后得到的。
查表时还要指定自由度。
t分布表使用的一个例子:
在99%的置信度下,对容量为14的样本作出一个估计。
解:从A=0.10那一栏下,找到自由度为13(n-1=14-1=13)那一行相交的数字,这个数字为1.771。数值1.771表明,如果从平均数两侧分别加减1.771个标准差,那么,在这两个界限之内曲线下的面积是99%,而有曲线面积之外是10%。如下图所示:
二、>2分布
>2分布的产生和适用范围简介:>2分布是海尔墨特(Hermert)和卡.皮尔生(K.Pearson)分别于1875年和1890年导出的。
它主要适用于对拟合优度检验和独立性检验,以及对总体方差的估计和检验等。
>2分布介绍:当我们对正态随机变量X随机地重复抽取n个数值,将每一个x值变换成标准正态变量,并对这n个新的变量分别取平方再求和之后,就得到一个服从自由度为n的>2分布。 >2分布的变量。即:
(一)分布具有以下几个特点:
1、>2分布是一个以自由度n为参数的分布族,自由度n决定了分布的形状,对于不同的n有不同的>2分布。
2、>2分布是一种非对称分布。一般为正偏分布。
3、>2分布的变量值始终为正。
4、分布的平均值为n,方差为2n。
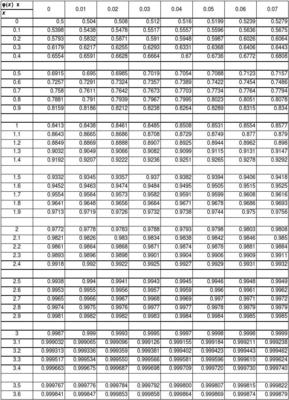
(二)>2分布表的使用
在表体中给出的是与表的左端列中所列出的各具体自由度数相对应的>2值。该值所切断的>2分布的右端尾部所包括的面积的比例,列在表的上端横行中。
如果n=10,,
也就是说,对于9个自由度,得到的检验统计量>2的值大于或等于18.31的概率为5%.
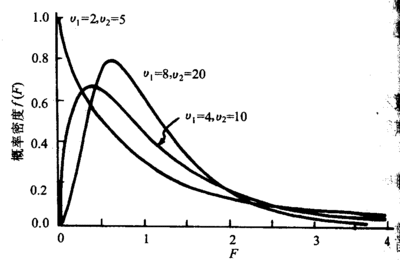
三、F分布
F分布: F分布是以统计学家R.A.Fisher姓氏的第一个字母命名的.
F分布的用途:用于方差分析、协方差分析和回归分析等。
(一)F分布定义为:设X、Y为两个独立的随机变量,X服从自由度为k1的>2分布,Y服从自由度为k2的>2分布,这2个独立的>2分布被各自的自由度除以后的比率这一统计量的分布。即:
上式F服从第一自由度为k1,第二自由度为k2的F分布
 爱华网
爱华网