扇形面积公式、圆柱、圆锥侧面展开图 圆锥侧面展开图

扇形面积公式、圆柱、圆锥侧面展开图

九年级数学同步辅导 2009-07-01 05:58:56 阅读18051 评论2 字号：大中小订阅

［学习目标］

1. 掌握基本概念：正多边形，正多边形的中心角、半径、边心距以及平面镶嵌等。

2. 扇形面积公式：

n是圆心角度数，R是扇形半径，l是扇形中弧长。

3. 圆柱是由矩形绕一边旋转360°形成的几何体，侧面展开是矩形，长为底面圆周长，宽为圆柱的高

r底面半径 h圆柱高

4. 圆锥侧面积

圆锥是由直角三角形绕一直角边旋转360°形成的几何体。

侧面展开是扇形，扇形半径是圆锥的母线，弧长是底面圆周长。

5. 了解圆柱由两平行圆面和一曲面围成，明确圆柱的高和母线，它们相等。

6. 了解圆锥由一个曲面和一个底面圆围成，明确圆锥的高和母线，知道可以通过解高、母线、底面半径所围直角三角形，解决圆锥的有关问题。

7. 圆柱

圆柱的侧面展开图是两邻边分别为圆柱的高和圆柱底面周长的矩形。圆柱的侧面积等于底面周长乘以圆柱的高。如图所示，若圆柱的底面半径为r，高为h，则：，。

8. 圆锥

圆锥是由一个底面和一个侧面组成的。圆锥的底面是一个圆，侧面是一个曲面，这个曲面在一个平面上展开后是一个扇形，这个扇形的半径是圆锥的母线，扇形的弧长是圆锥底面的周长。因此，圆锥的侧面积是圆锥的母线与底面周长积的一半。如图所示，若圆锥的底面半径为r，母线长为l，则

。

［重点、难点］

扇形面积公式及圆柱、圆锥侧面积公式的理解和灵活应用。

【典型例题】

例1. 已知如图1，矩形ABCD中，AB＝1cm，BC＝2cm，以B为圆心，BC为半径作圆弧交AD于F，交BA延长线于E，求扇形BCE被矩形所截剩余部分的面积。

图1

解：∵AB＝1，BC＝2，F点在以B为圆心，

BC为半径的圆上，

∴BF＝2，∴在Rt△ABF中，∠AFB＝30°，∠ABF＝60°

∴

例2. 已知扇形的圆心角150°，弧长为，则扇形的面积为____________。

解：设扇形的面积为S，弧长为l，所在圆的半径为R，

由弧长公式，得：

∴

由扇形面积公式，，故填。

点拨：本题主要考查弧长公式和扇形面积公式。

例3. 已知弓形的弦长等于半径R，则此弓形的面积为__________。（弓形的弧为劣弧）。

解：∵弓形弦长等于半径R

∴弓形的弧所对的圆心角为60°

∴扇形的面积为。

三角形的面积为。

∴弓形的面积为。

即。故应填。

点拨：注意弓形面积的计算方法，即弓形的面积等于扇形面积与三角形面积的和或差。本题若没有括号里的条件，则有两种情况。

例4. 若圆锥的母线与底面直径都等于a，这个圆锥的侧面积为_____________。

解：∵圆锥的底面直径等于a。

∴底面半径为，

∴底面圆的周长为。

又∵圆锥的母线长为a，

∴圆锥的侧面积为。

故应填

点拨：圆锥的侧面积即展开图的扇形面积，可利用扇形的面积公式求得。

例5. 如图2所示，OA和OO₁是⊙O中互相 垂直的半径，B在上，弧的圆心是O₁，半径是OO₁，⊙O₂与⊙O、⊙O₁、OA都相切，OO₁＝6，求图中阴影部分的面积。

图2

解：设⊙O₂与⊙O、⊙O₁、OA分别切于点D、C、E，设⊙O₂的半径为r，连结O₁O₂，O₂E，过点O₂作O₂F⊥O₁O于F，连结O₁B、OB、OO₂。

∵O₁O＝6，

l∴

∴

又∵

，

∴，

，

，

∴（舍去）

又∵是等边三角形

，

∴扇形和扇形的面积相等且都等于。

∴所组成的图形面积为扇形O₁BO和扇形OO₁B的面积之和减去三角形O₁OB的面积，即：

又∵扇形OAO₁的面积为：

∴阴影部分的面积为：

点拨：本题比较复杂，考查的知识面比较多，要正确作辅助线，找出解题的思路。

例6. 在半径为2的圆内，引两条平行弦，它们所对的弧分别为120°和60°，求两弦间所夹图形的面积及周长。

解：分两条弦在圆心的同侧或两侧这两种情况：

①如图3所示，由题意，

图3

则∠AOB＝120°，∠COD＝60°

又∵AB∥CD，

∴，

∴∠AOC＝∠BOD

又∵∠AOC＋∠BOD＝180°

∴∠AOC＝∠BOD＝90°

∴

又∵

故所求面积为

又∵∠AOC＝90°，

∴，

同理

又∵△OCD是等边三角形，

∴CD＝OC＝OD＝2

又∵

∴所求的周长

②如图4所示，由第一种情况，得所求面积：

图4

所求周长

点拨：要注意本题的两种情况，另外，弧长公式和扇形以及弓形的面积求法要求正确掌握，熟练运用。

例7. 如图5所示，已知正方形的边长是4cm，求它的内切圆与外接圆组成的圆环的面积。（答案保留）

（1999年广州）

图5

解：设正方形外接圆、内切圆的半径为R、r，面积为

。

∵

∴。

常见错误：此题最容易产生的问题是找不出正方形边长的一半与两圆的半径之间的勾股关系。即不会运用圆内接正方形与圆外切正方形的性质来解题。这一点读者应认真体会。

例8. 如图6所示，已知△ABC内接于⊙O，且AB＝BC＝CA＝6cm

图6

（1）求证：∠OBC＝30°；

（2）求OB的长（结果保留根号）；

（3）求图中阴影部分的面积（结果保留）。

解：（1）AB＝BC＝CA，∴∠A＝60°

∴∠BOC＝120°，又∵OB＝OC，

∴∠OBC

（2）过O作OD⊥BC于D，

∵OB＝OC，BC＝6cm，

∴

∵，

∴

（3）∵

∴

即阴影部分面积是。

常见错误：此题常见的问题是不会运用正三角形这一条件，从而无法证明∠OBC＝30°；当然，解直角三角形失误，求扇形面积时公式记错产生的错误，也是考试中的常见错误，应引起警惕。

例9. 一个圆锥的高是10cm，侧面展开图是半圆，求圆锥的侧面积。

点悟：如图7所示，欲求圆锥的侧面积，即求母线长l，底面半径r。由圆锥的形成过程可知，圆锥的高、母线和底面半径构成直角三角形即Rt△SOA，且SO＝10，SA＝l，OA＝r，关键找出l与r的关系，又其侧面展开图是半圆，可得关系，即。

图7

解：设圆锥底面半径为r，扇形弧长为C，母线长为l，

由题意得

∴ ①

在Rt△SOA中， ②

由①、②得：。

∴所求圆锥的侧面积为

。

例10. 圆锥的轴截面是等腰△PAB，且PA＝PB＝3，AB＝2，M是AB上一点，且PM＝2，那么在锥面上A、M两点间的最短距离是多少？

点悟：设圆锥的侧面展开图是扇形PBB'，A点落在A'点，则所求A'、M之间的最短距离就是侧面展形图中线段A'M的长度。

解：如图8所示，扇形的圆心角＝360°

图8

∴∠A'PB＝60°，在△A'PM中，过A'作A'N⊥PM于N，

则

∴，

【模拟试题】（答题时间：40分钟）

一、填表

（1）已知：正n边形边长为a

（2）已知：正n边形半径R

二、填空题：

1.如果扇形半径长3cm，圆心角120°，则它的面积是_____________cm²。

2.若圆锥母线长5cm，高3cm，则其侧面展开图的圆心角是_____________度。

3.若圆锥底面半径为3cm，母线长5cm，则它的侧面展开图面积是_____________cm²。

4.有一圆柱状玻璃杯，底面半径3cm，高为8cm，今有一长12cm的吸管斜放入杯中，若不考虑吸管粗细，则吸管最少露出杯口处的长度是_____________cm。

5.用一个半径为30cm，圆心角为120°的扇形纸片做成一圆锥侧面，那么圆锥底面半径是_____________cm。

6.如图1，正方形ABCD边长为2，分别以AB、BC为直径在正方形内作半圆，则图中阴影部分面积为_____________平方单位。

图1

7.如图2，AB＝2cm，∠AOB＝90°，AO＝BO，以O为圆心，OA为半径作弧AB，以AB为直径做半圆AmB，则半圆和弧AB所围阴影部分面积是_____________cm²。

图2

8.若圆锥侧面积为，母线长5cm，则圆锥的高为_____________cm。

9.圆柱表面积为，它的高为2cm，则底面半径为_____________cm。

10.矩形ABCD中，AC＝4cm，∠ACB＝30°，以直线AB为轴旋转一周，得到圆柱表面积为_____________cm²。

三、解答题：

11.已知扇形的半径为，它的面积恰好等于一个半径为的圆面积，那么这个扇形的圆心角为多少度？

12.如图3，已知半圆O，以AD为直径，AD＝2cm，B、C是半圆弧的三等分点，求图中阴影部分面积。

图3

13.已知如图，割线PCD过圆心O，且PD＝3PC，PA、PB切⊙O于点A、B，∠PAB＝60°，PA＝，AB与PD相交于E，求弓形ACB的面积。

【试题答案】

一、填表：

（1）

（2）

正n边形	中心角	半径	边心距	周长	面积
n＝3	120°
n＝4	90°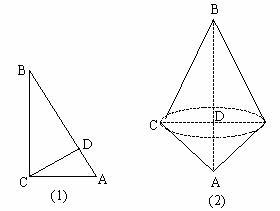
n＝6	60°	R		6R

二、填空题：

1. 2.2883.

4.25.106.

7.18.4cm9. 3cm

10.

三、解答题：

11. 解：由题意，设所求圆心角为°，则

答：所求扇形圆心角为60°

12. 解：连结OB、OC

∵

∴

13. 解：连结OA、OB，在Rt△AEP中，∠PAB＝60°

∴∠APD＝30°

在Rt△OAP中，

∴∠AOP＝60°，OA＝4，PO＝8

∴∠AOB＝120°

∴

由题意，PD＝3PC

∴

PC＝4，PD＝12

∴CD＝8

由题意：

∴

∴OE＝3

∴

∴

爱华网本文地址 » http://www.aihuau.com/a/25101015/248645.html