学习了资本资产定价模型,感觉书上的思路很凌乱,我看了好几遍终于觉得自己弄明白了
整理了一下思路,把我自己的关于capm的理解和思路记录下来
首先的假设是对人的假设:投资者是逐利的,而且是风险厌恶的。投资者是信息完全对称的,决策是趋同和可定性预测的。这就是所谓的马克维茨型投资者。
那么capm的目的是什么呢?是对某一种资产的应有的价值做出判断。
我们知道资产的价值在于预期,在于他在未来能够给予我们的回报,即是收益的问题,所以capm的一个核心使命,就是解决这个收益的最概然值以及收益对最概然值的收敛程度,即是收益率的大小和风险
对于投资有两个基本的前提认识
第一,投资由于放弃了即期消费,那么需要的到对机会成本的补偿,这体现为资金的时间价值,这对应与投资中的无风险投资(如国债这些东西),这个无风险收益率是一个对时间价值的补偿;
第二,选择了一个投资选择,那么就会承担风险,风险会要求汇报,这就是风险溢价;
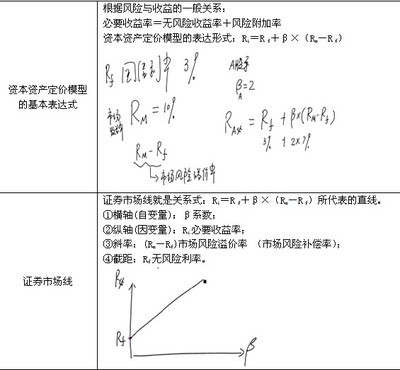
这里提到了两个基本的元素,即是收益和风险,首先来对他们建立数学描述。收益使用收益率的数学期望,风险用方差,来描述。
那么某一个证券的应有的收益,应该就是投入它的资金的时间价值加上它的风险带来的溢价的和。时间价值很容易判断,因为市场上的利率参考,或者国债利率,就可以作为无风险的收益,来反应资金的时间价值
那么风险溢价的情况呢?风险溢价才是证券之所以各有区别的原因,才是我们考虑问题的关键,每个证券的风险是多大?它带来的溢价率是多少?这是capm需要明确的一个问题。
关于风险和溢价,不是一个绝对问题,因为这是和市场相关的,价值永远是一个相对的概念,单个证券的风险和溢价是大幅度波动,且没有一个收敛点,但是整个市场的风险和溢价,是有规律可循的。在马克维茨的模型中也可以看到,对于组合的投资,风险是可以控制而收益可以提高,在最理想的情况下有一个投资组合,这就是capm中提到的市场组合。以市场组合为参照点,我们可以分析单个证券的收益和风险情况。
那么考虑投资市场组合,由于在市场组合中,各个证券都会对收益提供自己的分量,对风险也会提供自己的贡献。
1.有简单的数学计算可以看出,对组合的收益的贡献量等于此证券自己单独收益率乘以在组合中的权重。
2.单个证券对风险的贡献需要明确思路:投资的目标是市场组合,所以此风险不是单个证券自己的风险,而是该证券引入后引起的组合的风险的变化,换成数学语言就是:引入该证券后引起的组合的方差的变化。通过数学计算可以得到,这个方差的变化等于该证券和组合的协方差乘以权重。也就是说风险可以用这个协方差来表示。
3.关于风险的溢价率,则是因为市场是一个整体,对于投资者来说组合也好,单独的证券也好,相同的风险必然要求相同的溢价,也就是说单独证券的溢价率等于组合的溢价率。
由此,以市场组合为参照点,可以得到每个证券的风险溢价,加上本来的无风险收益(即是时间价值),就得到了该证券的应得收益率。
当然从另外一个方向来整理思路,即通过马克维茨组合投资的数学模型以及投资者效用曲线,可以找到我们需要作为参考点的市场组合点,这个点就是无风险点向有效区的切线的切点。
投资策略和融资策略也是在资本市场线上面。
这个策略加上对单个证券的评判,就构成了capm的大体概略。
当然,无论从哪个方向看capm,它都是自洽的一个逻辑系统,其自洽的根本原因在于,模型假设假设了市场的完全有效和信息完全对称,投资者完全理性和行为趋同,且可以定量的预测,没有外界对市场的扰动。一个封闭的完全可预测的系统当然可以建立自洽的数学模型,当然是可以定量描述。
这也是模型理想化的地方,也是和现实情况相背离的地方,对于现实的非有效市场和个性话的不可预测的投资者,capm具有一定的指导意义 ,但是失效的情况更加普遍。
 爱华网
爱华网