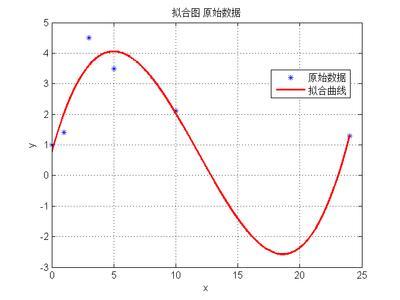
在许多数据处理过程中,需要猜想并找到其内在的数学关系即《数学模型》!
对于不能由理论推导得到结论的可采用曲线拟合的方法得到解决。
将数据X=x(i),Y=y(i)调入工作区,在MATLAB commandwindow窗口输入cftool(X,Y)出现曲线拟合窗口。
依据曲线大致形状判定采用哪种数学模型后,就可以拟合得到结果了。
例如: 人口预测问题,x是1979到2010的年份,y是每年的人口总数
Y=[0.0314 0.0333 0.0367 0.0450 0.05950.0741 0.0882 0.0936 0.1054 0.1201 0.1416 0.16780.2268 0.2680 0.3360 0.41270.4491 0.4829 0.5278 0.5803 0.6326 0.7012 0.7246 0.7466 0.77830.8008 0.82770.8711 0.9124 0.95430.99501.0372];数据乘1.0e+003。
X=1979:2010;
解:准备题目数据X Y
在MATLAB commandwindow窗口输入cftool(X,Y)出现曲线拟合窗口。
图1
依据曲线大致形状判定采用哪种数学模型后,就可以拟合得到结果了。
点击fitting按钮得下图2
图2
(1)点击“New fit”按钮,可修改拟合项目名称“Fit name”,通过“Data set”下拉菜单选择数据集,然后通过下拉菜单“Type of fit”选择拟合曲线的类型,工具箱提供的拟合类型有:
Custom Equations:用户自定义的函数类型
Exponential:指数逼近,有2种类型,a*exp(b*x) 、 a*exp(b*x) +c*exp(d*x)
Fourier:傅立叶逼近,有7种类型,基础型是a0 + a1*cos(x*w) +b1*sin(x*w)
Gaussian:高斯逼近,有8种类型,基础型是a1*exp(-((x-b1)/c1)^2)
Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving
Polynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~
Power:幂逼近,有2种类型,a*x^b 、a*x^b + c
Rational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~;此外,分子还包括constant型
Smoothing Spline:平滑逼近
Sumof Sin Functions:正弦曲线逼近,有8种类型,基础型是a1*sin(b1*x + c1)
Weibull:只有一种,a*b*x^(b-1)*exp(-a*x^b)
在type of fit选项中找到符合要求的选项Gaussian(高斯法)后点击Apply键。得下图3。
图3
在Results中可以查到你想要的结果了
拟合结果见图4
图4
(2)点击图2中的New fit选项,在type of fit选项中找到符合要求的选项Exponetial后点击Apply键。得图5
图5
在Results中可以查到你想要的结果了。截图中显示了a、b的值,全部情况可按滑动按钮查询。
拟合结果见图6
图6
通过不同形式的拟合,在多种实验结果中找到最佳拟合。
 爱华网
爱华网



