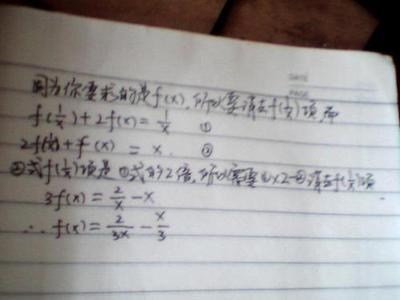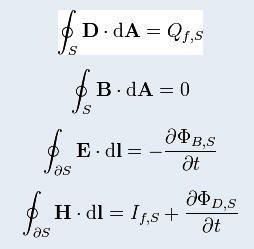
高斯定理
高斯定律(Gauss'law)表明在闭合曲面内的电荷分布与产生的电场之间的关系
由曲面向外定义为其方向,为闭合曲面内的电荷,为真空电容率,为此处电介质的介电常数(如果是真空的话,其数值为1)。其微分形式;其中,为电荷密度(单位C/m3)。在线性材料中,等式变为。其中为材料的电容率。
1基本定义
高斯定理(GaussLaw)也称为高斯公式(GaussFormula),或称作散度定理、高斯散度定理、高斯-奥斯特罗格拉德斯基公式、奥氏定理或高-奥公式(通常情况的高斯定理都是指该定理,也有其它同名定理)。
设空间有界闭合区域Ω,其边界∂Ω为分片光滑闭曲面。函数P(x,y,z)、Q(x,y,z)、R(x,y,z)及其一阶偏导数在Ω上连续,那么[1]:
图一(高数上的高斯公式)
(由于百科不支持很多格式及字符,故本词条使用一些截图,本公式请见右侧图一)
(如图一)其中∂Ω的正侧为外侧,cosα、cosβ、cosγ为∂Ω的外法向量的方向余弦。
高斯投影
称向量场的散度(divergence)。[1]
即矢量穿过任意闭合曲面的通量等于矢量的散度对闭合面所包围的体积的积分。它给出了闭曲面积分和相应体积分的积分变换关系,是矢量分析中的重要恒等式,也是研究场的重要公式之一。
2其它高斯定理
高斯定理2
定理:凡有理整方程
至少有一个根。
推论:一元n次方程
有且只有n个根(包括虚根和重根)。
高斯定理3
正整数n可被表示为两整数平方和的充要条件为n的一切形如4k+3形状的质因子的幂次均为偶数。
3物理定义与应用
矢量分析
矢量分析的重要定理之一。
图二(电场的高斯公式)
穿过一封闭曲面的电通量与封闭曲面所包围的电荷量成正比(公式如图二)。
换一种说法:电场强度在一封闭曲面上的面积分与封闭曲面所包围的电荷量成正比。
由于磁力线总是闭合曲线,因此任何一条进入一个闭合曲面的磁力线必定会从曲面内部出来,否则这条磁力线就不会闭合起来了。如果对于一个闭合曲面,定义向外为正法线的指向,则进入曲面的磁通量为负,出来的磁通量为正,那么就可以得到通过一个闭合曲面的总磁通量为0。这个规律类似于电场中的高斯定理,因此也称为高斯定理[2]。
与静电场中的高斯定理相比较,两者有着本质上的区别。在静电场中,由于自然界中存在着独立的电荷,所以电场线有起点和终点,只要闭合面内有净余的正(或负)电荷,穿过闭合面的电通量就不等于零,即静电场是有源场;而在磁场中,由于自然界中没有单独的磁极存在,N极和S极是不能分离的,磁感线都是无头无尾的闭合线,所以通过任何闭合面的磁通量必等于零。
电场E(矢量)通过任一闭曲面的通量,即对该曲面的积分等于该曲面所包围的总电荷量除以真空介电常数。公式表达:
给予空间的某个区域内,任意位置的电场。原则上,应用高斯定律,可以很容易地计算出电荷的分布。只要积分电场于任意区域的表面,再乘以真空电容率,就可以得到那区域内的电荷数量。
但是,更常遇到的是逆反问题。给予电荷的分布,求算在某位置的电场。这问题比较难解析。虽然知道穿过某一个闭合曲面的电通量,这资料仍旧不足以解析问题。在闭合曲面任意位置的电场可能会是非常的复杂。
假若,问题本身显示出某种对称性,促使在闭合曲面位置的电场大小变得均匀。那么,就可以借着这均匀性来计算电场。像圆柱对称、平面对称、球对称等等,这些空间的对称性,都能帮助高斯定律来解析问题。[1]
适用条件
任何电场
静电场(见电场)的基本方程之一,它给出了电场强度在任意封闭曲面上的面积分和包围在封闭曲面内的总电量之间的关系。
根据库仑定律可以证明电场强度对任意封闭曲面的通量正比于该封闭曲面内电荷的代数和,即公式
这就是高斯定理。它表示,电场强度对任意封闭曲面的通量只取决于该封闭曲面内电荷的代数和,与曲面内电荷的分布情况无关,与封闭曲面外的电荷亦无关。在真空的情况下,Σq是包围在封闭曲面内的自由电荷的代数和。当存在介质时,Σq应理解为包围在封闭曲面内的自由电荷和极化电荷的总和。
高斯定理反映了静电场是有源场这一特性。凡是有正电荷的地方,必有电力线发出;凡是有负电荷的地方,必有电力线会聚。正电荷是电力线的源头,负电荷是电力线的尾闾。
高斯定理是从库仑定律直接导出的,它完全依赖于电荷间作用力的二次方反比律。把高斯定理应用于处【】在静电平衡条件下的金属导体,就得到导体内部无净电荷的结论,因而测定导体内部是否有净电荷是检验库仑定律的重要方法。
对于某些对称分布的电场,如均匀带电球的电场,无限大均匀带电面的电场以及无限长均匀带电圆柱的电场,可直接用高斯定理计算它们的电场强度。
当存在电介质并用电位移D描写电场时,高斯定理可表示成▽·D=ρ。
它说明电位移对任意封闭曲面的通量只取决于曲面内自由电荷的代数和Σqo,与自由电荷的分布情况无关,与极化电荷亦无关。电位移对任一面积的能量为电通量,因而电位移亦称电通密度。对于各向同性的线性的电介质,电位移与电场强度成正比,D=εrεoE,εr称为介质的相对介电常数,这是一个无量纲的量。如果整个封闭曲面S在一均匀的相对介电常数为εr的线性介质中(其余空间区域可以充任何介质),高斯定理(2)又可写成在研究电介质中的静电场时,这两种形式的高斯定理特别重要。
高斯定理的微分形式为:(图三图四)
 爱华网
爱华网