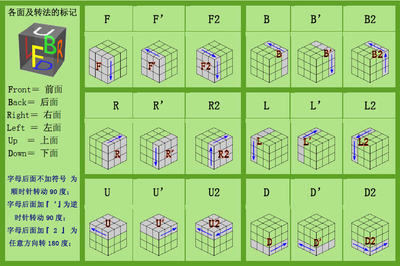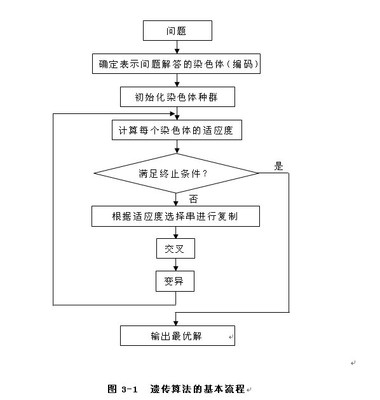
evalops是传递给适应度函数的参数,opts是二进制编码的精度,termops是选择maxGenTerm结束函数时传递个maxGenTerm的参数,即遗传代数。xoverops是传递给交叉函数的参数。mutops是传递给变异函数的参数。%郭涛算法_多父体杂交算法和郭涛算法_精英多父体杂交算法分别20次数值实验,并给出平均时间clear all;N=50;%初始个体个数M=8;n=1;%论域维数,可修改,用循环做eps=1e-6;%精度upper=10;lower=-10;%论域范围drop=upper-lower;%郭涛算法_多父体杂交算法minP0=zeros(20,n);minQ0=zeros(20,1);minFrequency0=zeros(20,1);minTimes0=zeros(20,1);for i=1:20 [minP0(i,:),minQ0(i),minFrequency0(i),minTimes0(i)]=GT(N,M,n,upper,lower,eps);end%对minP、minQ、minF requency按minQ从小到打排序tempP=zeros(20,n);tempFrequency=zeros(20,1);[X,I]=sort(minQ0);for r=1:20 tempP(r,:)=minP0(I(r),:); tempFrequency(r)=minFrequency0(I(r));endminP0=tempP;minQ0=X;minFrequency0=tempFrequency;averageTime0=sum(minTimes0)/20;averageFrequency0=sum(minFrequency0)/20;%郭涛算法_精英多父体杂交算法minP1=zeros(20,n);minQ1=zeros(20,1);minFrequency1=zeros(20,1);minTimes1=zeros(20,1);for i=1:20 [minP1(i,:),minQ1(i),minFrequency1(i),minTimes1(i)]=GT_GYZJ(N,M,n,upper,lower,eps);end%对minP、minQ、minFrequency按minQ从小到打排序tempP=zeros(20,n);tempFrequency=zeros(20,1);[X,I]=sort(minQ1);for r=1:20 tempP(r,:)=minP1(I(r),:); tempFrequency(r)=minFrequency1(I(r));endminP1=tempP;minQ1=X;minFrequency1=tempFrequency;averageTime1=sum(minTimes1)/20;averageFrequency1=sum(minFrequency1)/20;________________________________________________________________________________%郭涛算法_多父体杂交算法function[P_Best,Best,Frequency,Time]=GT(N,M,n,upper,lower,eps)if nargin<6 disp('输入参数错误'); return;elseif nargout<4 disp('输出参数错误'); return;end drop=upper-lower;%若各个分量上下界不同,可以用数组来代替P=zeros(N,n);%存放初始N个个体,每个个体有n个基因位Q=zeros(N,1);%存放P中个体对应函数值Frequency =0;%当前比较次数tic%生成初始群体Pfor s=1:n P(:,s)=drop*rand(N,1)+lower;end%生成初始群体P对应的函数值for r=1:N Q(r)=f(P(r,:));end[Best,BestIndex]=min(Q);[Worst,WorstIndex]=max(Q);%以下为郭涛算法主体循环部分A=zeros(1,M);B=zeros(1,M);while Worst-Best>eps Frequency=Frequency+1; %从P中选M个个体生成空间V,其下标存放于A中 A=floor(rand(1,M)*(N-1))+1; %生成Xson的各个组合系数(待检测) sum=0;minbound=-0.5;maxbound=1.5; for r=1:M-1 B(r)=(maxbound-minbound)*rand(1)+minbound; sum=sum+B(r); maxbound=min(1.5,1.5-sum); minbound=max(-0.5,-0.5-sum); end B(M)=1-sum; %生成Xson Xson=zeros(1,n); for r=1:M Xson=Xson+B(r)*P(A(r),:); end %越界处理 for s=1:n if Xson(s)<lower Xson(s)=lower; elseif Xson(s)>upper Xson(s)=upper; end end y=f(Xson); ify<Worst P(WorstIndex,:)=Xson;Q(WorstIndex)=y; [Best,BestIndex]=min(Q); [Worst,WorstIndex]=max(Q); end endP_Best=P(BestIndex,:);Time=toc;________________________________________________________________________________%郭涛算法_精英多父体杂交算法function[P_Best,Best,Frequency,Time]=GT_GYZJ(N,M,n,upper,lower,eps)if nargin<6 disp('输入参数错误'); return;elseif nargout<4 disp('输出参数错误'); return;end drop=upper-lower;%若各个分量上下界不同,可以用数组来代替P=zeros(N,n);%存放初始N个个体,每个个体有n个基因位Q=zeros(N,1);%存放P中个体对应函数值Frequency =0;%当前比较次数tic%生成初始群体Pfor s=1:n P(:,s)=drop*rand(N,1)+lower;end%生成初始群体P对应的函数值for r=1:N Q(r)=f(P(r,:));end[Best,BestIndex]=min(Q);[Worst,WorstIndex]=max(Q);%以下为郭涛算法主体循环部分A=zeros(1,M);B=zeros(1,M);while Worst-Best>eps Frequency=Frequency+1; [m,A(1)]=min(Q); %从P中选M-1个个体生成空间V,其下标存放于A中 A(2:end)=floor(rand(1,M-1)*(N-1))+1; %生成Xson的各个组合系数(待检测) sum=0;minbound=-0.5;maxbound=1.5; for r=1:M-1 B(r)=(maxbound-minbound)*rand(1)+minbound; sum=sum+B(r); maxbound=min(1.5,1.5-sum); minbound=max(-0.5,-0.5-sum); end B(M)=1-sum; %生成Xson Xson=zeros(1,n); for r=1:M Xson=Xson+B(r)*P(A(r),:); end %越界处理 for s=1:n if Xson(s)<lower Xson(s)=lower; elseif Xson(s)>upper Xson(s)=upper; end end y=f(Xson); ify<Worst P(WorstIndex,:)=Xson;Q(WorstIndex)=y; [Best,BestIndex]=min(Q); [Worst,WorstIndex]=max(Q); end endP_Best=P(BestIndex,:);Time=toc;________________________________________________________________________________%函数f(x)function y=f(x)n=length(x);y=1;for i=1:n s=0; for j=1:5 s=s+j*cos((j+1)*x(i)+j); end y=y*s;end
 爱华网
爱华网