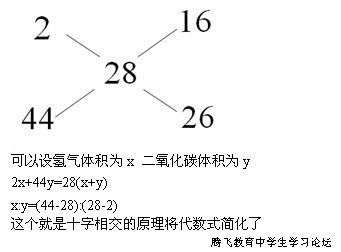
1.(1999年天津市数学竞赛题)当k为何值时,多项式x2-2xy+ky2+3x-5y+2能分解成两个一次因式的积?
刚看到这个题目的想法是:既然可以分解成两个一次因式的积,那必然是(x+ay+1)(x+by+2)形式。因为2=1×2=(-1)×(-2),那到底是哪个呢?观察3x的系数是+3,所以选1和2。突然发现,这跟十字相乘法很像。所以,赶紧把这道题先做成了再说。算出k=-3。然后再回代,好像也不知道什么?
继续做类似的题目:
2.(第18届五羊杯竞赛题)分解因式:2x2-xy-6y2+7x+7y+3=
咦,有点像刚才那题目,先分解成:(2x+…+1)(x+…+3)的形式,这里的y应该要怎么做,是不是也可以用十字相乘法,试了再说吧。正好,-6y2+7y+3=(3y+1)(-2y+3)。咦,那正好,代了再说吧。就变成了(2x+3y+1)(x-2y+3),是不是呢?再把它算出来,结果对了!
好!既然方法对了,再试一题对吗?
3.(第8届希望杯竞赛题)分解因式:x2-y2-2x-4y-3=
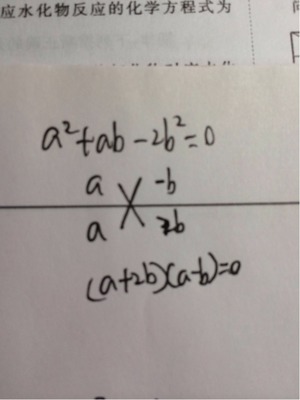
那应该是(x+y+1)(x-y-3),跟答案一对,对的!!哇。也这行?!!!
去网站查一下,居然也有。
原来这种方法就是双十字相乘法,也叫大十字相乘法。
方法是:先把原式看成两个二元一次方程的因式分解。如第2题:2x2-xy-6y2+7x+7y+3先把其看作:
2x2+7x+3和-6y2+7y+3作因式分解为(2x+1)(x+3)和(3y+1)(-2y+3)再把它们合在一块就变成了(x+3y+1)(x-2y+3).
原来双十字相乘法是建立在十字相乘法上的。
 爱华网
爱华网