标准偏差在误差理论、质量管理、计量型抽样检验等领域中均得到了广泛的应用。因此,标准偏差的计算十分重要, 它的准确与否对器具的不确定度、测量的不确定度以及所接收产品的质量有重要影响。然而在对标准偏差的计算中,不少人不论测量次数多少, 均按贝塞尔公式计算。
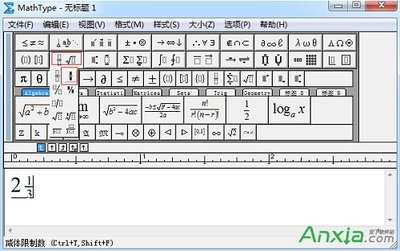
样本标准差的表示公式
数学表达式:
标准偏差的使用方法
标准偏差的计算步骤
标准偏差的计算步骤是:
步骤一、(每个样本数据 -样本全部数据之平均值)2。
步骤二、把步骤一所得的各个数值相加。
步骤三、把步骤二的结果除以 (n -1)(“n”指样本数目)。
步骤四、从步骤三所得的数值之平方根就是抽样的标准偏差。
六个计算标准偏差的公式[1]
标准偏差的理论计算公式
设对真值为X的某量进行一组等精度测量, 其测得值为l1、l2、……ln。令测得值l与该量真值X之差为真差占σ,则有 σ1 = li −X
σ2 =l2 − X
……
σn = ln −X
我们定义标准偏差(也称标准差)σ为
(1)
由于真值X都是不可知的,因此真差σ占也就无法求得,故式只有理论意义而无实用价值。
标准偏差σ的常用估计—贝塞尔公式
由于真值是不可知的, 在实际应用中,我们常用n次测量的算术平均值来代表真值。理论上也证明,随着测量次数的增多, 算术平均值最接近真值, 当时,算术平均值就是真值。
于是我们用测得值li与算术平均值之差——剩余误差(也叫残差)Vi来代替真差σ, 即
设一组等精度测量值为l1、l2、……ln
则
……
通过数学推导可得真差σ与剩余误差V的关系为
将上式代入式(1)有
(2)
式(2)就是著名的贝塞尔公式(Bessel)。
它用于有限次测量次数时标准偏差的计算。由于当时,,可见贝塞尔公式与σ的定义式(1)是完全一致的。
应该指出,在n有限时, 用贝塞尔公式所得到的是标准偏差σ的一个估计值。它不是总体标准偏差σ。因此,我们称式(2)为标准偏差σ的常用估计。为了强调这一点, 我们将σ的估计值用“S ”表示。于是, 将式(2)改写为
(2')
在求S时,为免去求算术平均值的麻烦,经数学推导(过程从略)有
于是,式(2')可写为
(2")
按式(2")求S时,只需求出各测得值的平方和和各测得值之和的平方艺, 即可。
标准偏差σ的无偏估计
数理统计中定义S2为样本方差
数学上已经证明S2是总体方差σ2的无偏估计。即在大量重复试验中,S2围绕σ2散布,它们之间没有系统误差。而式(2')在n有限时,S并不是总体标准偏差σ的无偏估计,也就是说S和σ之间存在系统误差。概率统计告诉我们, 对于服从正态分布的正态总体,总体标准偏差σ的无偏估计值为
(3)
令
则
即S1和S仅相差一个系数Kσ,Kσ是与样本个数测量次数有关的一个系数,Kσ值见表。
计算Kσ时用到
Γ(n + 1) =nΓ(n)
Γ(1) =1
由表1知,当n>30时, 。因此, 当n>30时, 式(3')和式(2')之间的差异可略而不计。在n=30~50时,最宜用贝塞尔公式求标准偏差。当n<10时, 由于Kσ值的影响已不可忽略, 宜用式(3'),求标准偏差。这时再用贝塞尔公式显然是不妥的。
标准偏差的最大似然估计
将σ的定义式(1)中的真值X用算术平均值代替且当n有限时就得到
(4)
式(4)适用于n>50时的情况,当n>50时,n和(n-1)对计算结果的影响就很小了。
2.5标准偏差σ的极差估计由于以上几个标准偏差的计算公式计算量较大,不宜现场采用, 而极差估计的方法则有运算简便, 计算量小宜于现场采用的特点。
极差用"R"表示。所谓极差就是从正态总体中随机抽取的n个样本测得值中的最大值与最小值之差。
若对某量作次等精度测量测得l1、,且它们服从正态分布,则
R =lmax −lmin
概率统计告诉我们用极差来估计总体标准偏差的计算公式为
(5)
S3称为标准偏差σ的无偏极差估计,d2为与样本个数n(测得值个数)有关的无偏极差系数,其值见表2
由表2知,当n≤15时,,因此, 标准偏差σ更粗略的估计值为
(5')
还可以看出,当200≤n≤1000时,因而又有
(5")
显然,不需查表利用式(5')和(5")了即可对标准偏差值作出快速估计,用以对用贝塞尔公式及其他公式的计算结果进行校核。
应指出,式(5)的准确度比用其他公式的准确度要低,但当5≤n≤15时,式(5)不仅大大提高了计算速度, 而且还颇为准确。当n>10时,由于舍去数据信息较多, 因此误差较大, 为了提高准确度, 这时应将测得值分成四个或五个一组, 先求出各组的极差R1、,再由各组极差求出极差平均值。
极差平均值和总体标准偏差的关系为
需指出,此时d2大小要用每组的数据个数n而不是用数据总数N(=nK)去查表2。再则,分组时一定要按测得值的先后顺序排列,不能打乱或颠倒。
标准偏差σ的平均误差估计
平均误差的定义为
误差理论给出
(A)
可以证明与的关系为
(证明从略)
于是 (B)
由式(A)和式(B)得
从而有
式(6)就是佩特斯(C.A.F.Peters.1856)公式。用该公式估计δ值,由于right|Vright|不需平方,故计算较为简便。但该式的准确度不如贝塞尔公式。该式使用条件与贝塞尔公式相似。
标准偏差的应用实例[1]
对标称值Ra = 0.160< math >μm < math> 的一块粗糙度样块进行检定,顺次测得以下15个数据:1.45,1.65,1.60,1.67,1.52,1.46,1.72,1.69,1.77,1.64,4.56,1.50,1.64,1.74和1.63μm,试求该样块Rn的平均值和标准偏差并判断其合格否。
解:1)先求平均值
2)再求标准偏差S
若用无偏极差估计公式式(5)计算, 首先将测得的, 15个数据按原顺序分为三组,每组五个, 见表3。
表3
组号 l_1 l_5 R 1 1.48 1.65 1.60 1.67 1.52 0.19 2 1.46 1.72 1.69 1.77 1.64 0.31 3 1.56 1.50 1.64 1.74 1.63 0.24
因每组为5个数据,按n=5由表2查得
故
若按常用估计即贝塞尔公式式(2') ,则
若按无偏估计公式即式(3')计算,因n=15,由表1查得Kδ =1.018, 则
若按最大似然估计公式即式(4')计算,则
= 0.09296(< math >μm < math> )
若按平均误差估计公式即式(6),则
现在用式(5')对以上计算进行校核
可见以上算得的S、S1、S2、S3和S4没有粗大误差。
由以上计算结果可知0.09296<0.0962<0.0979<0.1017<0.1062
即 S2 < S< S1 <S4 <S3
可见,最大似然估计值最小, 常用估计值S稍大, 无偏估计值S1又大,平均误差估计值S4再大,极差估计值S3最大。纵观这几个值, 它们相当接近,最大差值仅为0.01324μm。从理论上讲, 用无偏估计值和常用估计比较合适, 在本例中,它们仅相差0.0017μm。可以相信, 随着的增大,S、S1、S2、S3和S4之间的差别会越来越小。
就本例而言,无偏极差估计值S3和无偏估计值S1仅相差0.0083μm,这说明无偏极差估计是既可以保证一定准确度计算又简便的一种好方法。
JJG102-89《表面粗糙度比较样块》规定Ra的平均值对其标称值的偏离不应超过+12%~17%,标准偏差应在标称值的4%~12%之间。已得本样块二产,产均在规定范围之内,故该样块合格。
标准偏差与标准差的区别
标准差(StandardDeviation)各数据偏离平均数的距离(离均差)的平均数,它是离差平方和平均后的方根。用σ表示。因此,标准差也是一种平均数。标准差是方差的算术平方根。 标准差能反映一个数据集的离散程度。平均数相同的,标准差未必相同。
例如,A、B两组各有6位学生参加同一次语文测验,A组的分数为95、85、75、65、55、45,B组的分数为73、72、71、69、68、67。这两组的平均数都是70,但A组的标准差为17.08分,B组的标准差为2.16分,说明A组学生之间的差距要比B组学生之间的差距大得多。
标准偏差(StdDev,Standard Deviation) - 统计学名词。一种量度数据分布的分散程度之标准,用以衡量数据值偏离算术平均值的程度。标准偏差越小,这些值偏离平均值就越少,反之亦然。标准偏差的大小可通过标准偏差与平均值的倍率关系来衡量。
标准误差(Standarderror),也称均方根误差(Root mean squared error)
什么是标准误差
在相同测量条件下进行的测量称为等精度测量,例如在同样的条件下,用同一个游标卡尺测量铜棒的直径若干次,这就是等精度测量。对于等精度测量来说,还有一种更好的表示误差的方法,就是标准误差。
标准误差定义为各测量值误差的平方和的平均值的平方根,故又称为均方误差。
标准误差不仅是一组测量中各个测量值的函数,而且对一组测量中的较大误差或较小误差比较敏感,故它是表示准确度的较好方法。
标准误差的公式
设n个测量值的误差为E1、E2……En,则这组测量值的标准误差σ等于:
其中,E =Xi −T,式中:E-误差;Xi-测定值;T-真实值。
由于被测量的真值是未知数,各测量值的误差也都不知道,因此不能按上式求得标准误差。测量时能够得到的是算术平均值,它最接近真值(N),而且也容易算出测量值和算术平均值之差,称为残差(记为v)。理论分析表明可以用残差v表示有限次(n次)观测中的某一次测量结果的标准误差σ,其计算公式为:
对于一组等精度测量(n次测量)数据的算术平均值,其误差应该更小些。理论分析表明,它的算术平均值的标准误差。有的书中或计算器上用符号s表示):
标准误差的注意点
需要注意的是,标准误差不是测量值的实际误差,也不是误差范围,它只是对一组测量数据可靠性的估计。标准误差小,测量的可靠性大一些,反之,测量就不大可靠。进一步的分析表明,根据偶然误差的高斯理论,当一组测量值的标准误差为σ时,则其中的任何一个测量值的误差Ei有68.3%的可能性是在(-σ,+σ)区间内。
世界上多数国家的物理实验和正式的科学实验报告都是用标准误差评价数据的,现在稍好一些的计算器都有计算标准误差的功能,因此,了解标准误差是必要的。
标准差是一种表示分散程度的统计观念。标准差已广泛运用在股票以及共同基金投资风险的衡量上,主要是根据基金净值于一段时间内波动的情况计算而来的。一般而言,标准差愈大,表示净值的涨跌较剧烈,风险程度也较大。实务的运作上,可进一步运用单位风险报酬率的概念,同时将报酬率的风险因素考虑在内。所谓单位风险报酬率是指衡量投资人每承担一单位的风险,所能得到的报酬,以夏普指数最常为投资人运用。
标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
例如,两组数的集合 {0, 5, 9,14} 和 {5, 6, 8, 9} 其平均值都是 7 ,但第二个集合具有较小的标准差。
标准差可以当作不确定性的一种测量。例如在物理科学中,做重复性测量时,测量数值集合的标准差代表这些测量的精确度。当要决定测量值是否符合预测值,测量值的标准差占有决定性重要角色:如果测量平均值与预测值相差太远(同时与标准差数值做比较),则认为测量值与预测值互相矛盾。这很容易理解,因为值都落在一定数值范围之外,可以合理推论预测值是否正确。
标准差的简易计算公式
假设有一组数值 x1, ..., xN(皆为实数),其平均值为:
此组数值的标准差为:
一个较快求解的方式为:
一随机变量X的标准差定义为:
须注意并非所有随机变量都具有标准差,因为有些随机变量不存在期望值。如果随机变量X 为x1,...,xN 具有相同机率,则可用上述公式计算标准差。从一大组数值当中取出一样本数值组合 x1,...,xn,常定义其样本标准差:
范例:标准差的计算
这里示范如何计算一组数的标准差。例如一群孩童年龄的数值为{ 5, 6, 8, 9 } :
第一步,计算平均值
n = 4(因为集合里有 4 个数),分别设为:
用 4 取代 N
此为平均值。
第二步,计算标准差
用 4 取代 N
用7 取代
标准差与平均值之间的关系
一组数据的平均值及标准差常常同时做为参考的依据。在直觉上,如果数值的中心以平均值来考虑,则标准差为统计分布之一"自然"的测量。较确切的叙述为:假设x1, ..., xn 为实数,定义其公式
使用微积分,不难算出σ(r) 在下面情况下具有唯一最小值:
标准偏差与标准差的区别
标准差(StandardDeviation)各数据偏离平均数的距离(离均差)的平均数,它是离差平方和平均后的方根。用σ表示。因此,标准差也是一种平均数。标准差是方差的算术平方根。 标准差能反映一个数据集的离散程度。平均数相同的,标准差未必相同。
例如,A、B两组各有6位学生参加同一次语文测验,A组的分数为95、85、75、65、55、45,B组的分数为73、72、71、69、68、67。这两组的平均数都是70,但A组的标准差为17.08分,B组的标准差为2.16分,说明A组学生之间的差距要比B组学生之间的差距大得多。
标准偏差(StdDev,Standard Deviation) -统计学名词。一种量度数据分布的分散程度之标准,用以衡量数据值偏离算术平均值的程度。标准偏差越小,这些值偏离平均值就越少,反之亦然。标准偏差的大小可通过标准偏差与平均值的倍率关系来衡量。
中误差 英文名称:root mean squareerror;RMSE 定义:带权残差平方和的平均数的平方根,作为在一定条件下衡量测量精度的一种数值指标。
中误差是衡量测量精度的指标之一。亦称“标准误差”或“均方根差”。在相同观测条件下的一组真误差平方中数的平方根,真误差是观测值与真值之差。因真误差不易求得,所以通常用最小二乘法求得的观测值改正数(观测值与同观测条件下一组观测值平均数也称数学期望之差)来代替真误差。
 爱华网
爱华网