总是记不住微分电路和积分电路,所以觉得有必要整理一下相关资料
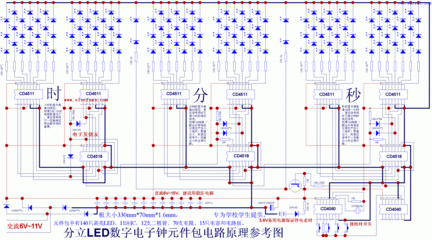
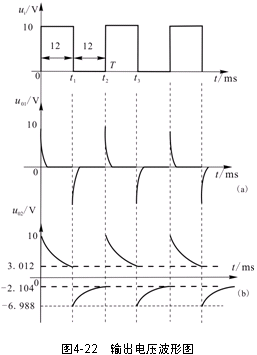
1.微分电路电路结构如图W-1,微分电路可把矩形波转换为尖脉冲波,此电路的输出波形只反映输入波形的突变部分,即只有输入波形发生突变的瞬间才有输出。而对恒定部分则没有输出。输出的尖脉冲波形的宽度与R*C有关(即电路的时间常数),R*C越小,尖脉冲波形越尖,反之则宽。此电路的R*C必须远远少于输入波形的宽度,否则就失去了波形变换的作用,变为一般的RC耦合电路了,一般R*C少于或等于输入波形宽度的1/10就可以了。
2.积分电路电路结构如图J-1,积分电路可将矩形脉冲波转换为锯齿波或三角波,还可将锯齿波转换为抛物波。电路原理很简单,都是基于电容的冲放电原理,这里就不详细说了,这里要提的是电路的时间常数R*C,
构成积分电路的条件是电路的时间常数必须要大于或等于10倍于输入波形的宽度。
积分和微分电路主要依靠的是电容的特性而发挥作用的
电容最基本的作用是充电和放电。
一个电容跟一个负载电阻的微分电路:
如果电容电压为0,负载阻抗较大,信号源内阻很小,并假设信号源开始
是0电平,然后突然出现一个到V的上跳,那么,这个上跳沿马上可以反应
到负载电阻上,即负载电阻在这时刻输出为V。然后电压慢慢降低。
电容两端的电压不能突变啊。不能突变,就相当于一根导线了
在边沿突变时,电容相当于短路。所以输出端会跟随输入端的。
相当于短路,是在假设电容两端没有电压的情况下。
如果电容已经被充上电,则可把它当作一个理想电源来分析
1865年麦克斯韦提出一个假设:当电容器充、放电时,电容器中的电场发生变化,变化的电场可等效为电流,这种电流称为位移电流,位移电流等于电位移通量随时间的变化率,某一时刻位移电流的大小和方向,就是该时刻电路中传导电流的大小和方向,在引入了位移电流后,电容器的充放电过程也就可以看成是闭合回路了,这样就使电流保持了连续性
对于有RC构成的积分电路来说,输出取自电容,输出电压是与电容上的电压成正比的。从电容特性知道,电容上的电压正比于它上面的电荷,而电容上的电荷是流过电容电流在时间上的积分(记住电流的概念是单位时间流过的电荷),所以输出电压正比于对电容电流的积分,故称积分电路。反过来,微分电路的输出是在电阻上取出的(关键的区别!!),根据欧姆定律,电 阻上的电压正比于流过电阻的电流,而流过电阻的电流也就是流过电容的电流。从上面讨论知道,流过电容的电流正比于电容上电压的微分,所以,输出电压正比于电容电压的微分,故称微分电路。
通过以上就应该可以理解微分和积分电路了,其实我一直对电容储存电荷又能流过电流很疑惑,这个位移电流很好的解释了这个疑问。
 爱华网
爱华网