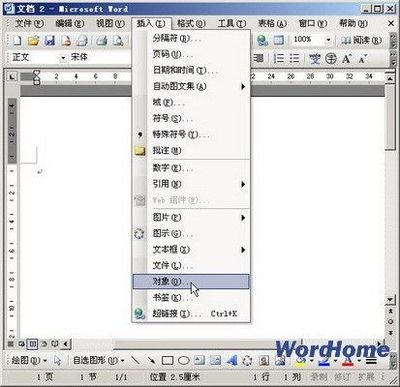
反馈开方公式
从网上找到一个牛B开方公式,如图
公式1
对A开k次方,A>0, k=2,3,4,5……
手算开方最适用的也就是开平方,开立方。开高次方本公式也适用,不过计算量大点。
你输入一个近似值X_n,输出值X_(n+1)会补偿部分误差,更接近准确值。多次迭代,达到或非常接近准确值。
即使X_n误差很大,X_(n+1)也更接近准确值,多次迭代,也能达到或非常接近准确值。这叫反馈开方。
推导过程如下
这个公式用牛顿切线法推导也行。
例如,A=5,k=3.
公式:X_(n+1)=X_n+(A/X_n^2-Xn)/3
5介于1^3至2^3之间(1的3次方=1,2的3次方=8)
初值 X_0可以取1.0,1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9,2.0。
例如我们取2.0 按照公式:
第一步:X_1=2.0+[5/(2.0^2-2.0]/3=1.75。
因为1.75与2.0偏差较大,所以1.75只取1.7就行,仍是两位数。有细心的读者问:1.75就算取两位数,也应该四舍五入到1.8呀?问得好!
我用Excel表格迭代反馈开方公式时,发现无论输入值比准确值大还是小,输出值都比准确值大。
[这个现象我以后专门证明]
也就是X_1=1.75比真实值大,所以1.75的5舍弃!
第二步:X_2=1.7+[5/(1.7^2-1.7]1/3=1.71003
因为1.71003与1.7偏差很小,所以取4位数,比前面多取两位数。
X_2=1.710
第三步:X_3=1.710+[5/(1.710^2-1.710]/3=1.709975947。
因为1.709975947与1.710偏差极小,所以甚至可取8位数,比前面多取4位数!
X_3=1.7099759
这种方法可以自动调节,第一步与第三步取值偏大,按照 反馈开方公式 输出值自动变小;
第二步输入值偏小,按照 反馈开方公式 输出值自动变大。
又如取 x_0=1.0
在Excel表格中复制公式,用迭代法
x_0=1→x_1=2.33333→1.86168→1.72200→1.71006→x_5=1.70998
看出问题了,x_1=2.33333这个正反馈值已经超过1-2的上限,虽然经过6次反馈也能得出很精确的值,但是比上面只经过3次反馈麻烦多了。
所以x_0的选择要严谨,初估值在1-2之间,如果靠近1就取1,如果靠近2就取2,
如果两个都不靠近,再确定<1.5还是>1.5,这样初估值就非常接近真实值
仍以A=5,k=3为例
初估值在1-2之间,判断中间值1.5大小:
1.5^3=3.375<5<8
所以1.5<初估值<2
并且3.375比8更靠近5,所以初估值1.6或1.7
例2:A=0.5,k=3
0<A<1,0和1之间的数开方,结果在A和1之间。0.7^3=0.343,0.8^3=0.512, 0.512很接近0.5,所以取初值
x_0=0.80,在Excel表格中复制公式,用迭代法
0.80→0.79375→0.7937005290677→0.7937005259841
只要 3步,就精确到13位有效数字,功劳首推初值精度高。
用乘方反过来验算
0.7937500000000 ^3 = 0.5000935058594
0.7937005290677 ^3 = 0.5000000058277
0.7937005259841 ^3 = 0.5000000000000
 爱华网
爱华网