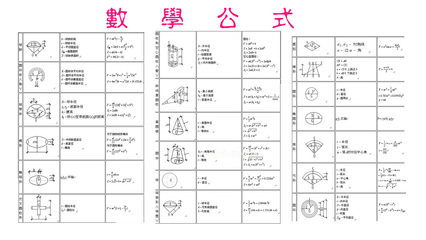
1.每份数×份数=总数 总数÷每份数=份数 总数÷份数=每份数
2.1倍数×倍数=几倍数 几倍数÷1倍数=倍数 几倍数÷倍数=1倍数
3.速度×时间=路程 路程÷速度=时间 路程÷时间=速度
4.单价×数量=总价 总价÷单价=数量 总价÷数量=单价
5.工效×工时=工总 工总÷工效=工时 工总÷工时=工效
6.加数+加数=和 和-一个加数=另一个加数
7.被减数-减数=差 被减数-差=减数 差+减数=被减数
8.因数×因数=积 积÷一个因数=另一个因数
9.被除数÷除数=商 被除数÷商=除数 商×除数=被除数
10.被除数÷除数=商……余数 商×除数+余数=被除数
典型例题例1
1.铅笔每枝5解,买3枝多少钱?
分析:铅笔每枝5角是单价,买3枝是数量,共用15角是总价。
解答:5×3=15(角)
2.每个足球62元,买两个同样的足球用去多少元?
分析:每个足球62元是单价,买2个是数量,共用124元是总价。
解答:62×2=124(元)
3.鲤鱼每千克6元,买4千克需多少元?
分析:每千克鲤鱼6元是单价,买4千克是数量,共用24元是总价。
解答:6×4=24(元)
小结:通过上面的例子,我们知道了每件商品的价钱叫单价,买多少商品叫数量,一共用多少钱叫总价。这三种量之间的关系是:单价×数量=总价。
例2
1.苹果树平均每棵收苹果25千克,5棵苹果树收多少千克?
分析:每棵苹果树收苹果24千克是单产量,5棵苹果树是数量,一共收的苹果重量是总产量。
解答:25×5=125(千克)
2.菜园每畦产菠菜150千克,4畦产菠菜多少于克?
分析:菜园每畦产菠菜150千克是单产量,4畦菠菜是数量,一共收菠菜的千克数是总产量。
解答:150×4=600(千克)
小结:单产量、数量、总产量这三种量之间的关系是:单产量×数量=总产量。
例3
1.汽车每小时行45千米,4小时行多少千米?
分析:汽车每小时行45千米是速度,行4小时是时间,行的总千米数是路程。
解答:45×4=180(千克)
2.火车每小时行65千米,3小时行多少千米?
分析:火车每小时行65千米是速度,行3小时是时间,行的总千米数是路程。
解答:65×3=195(千米)
小结:这三种量之间的关系是:速度×时间=路程。
例4 李师傅每小时生产30个零件,7小时生产多少个零件?
分析:每小时生产30个零件是工作效率,7小时是工作时间,共生产210个零件是工作总量。
解答:30×7=210(个)
小结:这三种量之间的关系是:工作效率×工作时间=工代总量。
习题精选一、判断下面各题的对错.
1.知道每份报纸的价钱和买的份数,求总价,应用报纸单价乘以份数。( )
2.知道每小时走的路程和走的时间,可以求走的速度。( )
3.车间有6台机床,平均一台机床每天生产零件400个————,此车间一天一共可以生产多少个零件?这道题是求工作总量的题目。( )
4.小利家到学校的距离是600米,恰好12分走到,每分走了多少米?是求路程的题目。( )
二、买了8筐萝卜,一共72千克,每千克8角,平均每筐萝卜多少钱?
算式:
三、1.用“7小时”编一道有关求路程的应用题,再解答出来。
2.用“买4个排球”编一道求总价的应用题,再解答出来。
3.用“8小时”编一道求工作总量的应用题,再解答出来。
参考答案一、1.( √) 2.( √ )3.( √ ) 4.(× )
二、算式:8×72
三、1.一辆汽车每小时跑80公里,7小时跑多少公里?
解:80×7 = 560(公里)
答:7小时跑560公里.
2.买1个排球要用26元,买4个排球要用多少元?
解:26×4=104(元)
答:买4个排球要用104元。
3.王师傅每小时生产零件18个,8小时一共生产零件多少个?
解:18×8=144(个)
答:8小时一共生产144个零件。
 爱华网
爱华网