天津市中小学信息技术课程教学设计案例
设计日期:2011 年 3 月 1 日
作者姓名 | 电子信箱 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
作者单位 | 宝坻区第四中学 | 区县 | 宝坻区 | ||||||||||||||||||||||||||||||||||||||||||||||||||
教案名称 | 递归法与问题解决 | 课时 | 2课时 | ||||||||||||||||||||||||||||||||||||||||||||||||||
教材版本 | 中国地图出版社 | 学生年级 | 高中一年级 | ||||||||||||||||||||||||||||||||||||||||||||||||||
一、教材内容分析 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
本节主要探讨使用“递归法”解决问题。第三单元“算法与问题解决”是《算法与程序设计》这本书的灵魂所在,而递归法与问题解决这一节又是第三单元的重中之重。本节通过阶乘的递归调用和梵诺塔问题的求解,探讨如何利用递归关系式将大问题转化为小问题,将小问题的解决作为突破口,进而使复杂的大问题得以解决。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
二、学生分析 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
学生对程序设计有了一定基础,对算法却是刚刚接触,如“解析法”和“穷举法”,而“递归法”还是一个全新的问题。建构主义理论认为学习是新旧知识的联系,是学习者主动建构内在心理结构的过程。本节内容具有一定的抽象性,而对于算法的初学者,如果直接讲递归算法,学生很难实现新旧知识的联系,无法做到意义建构和有意义的学习,对于递归算法的含义、递归算法的适用条件就难以做到真正把握。 这就要求在教学过程中设置身边能够实际接触到的问题(求年龄问题等),使学生产生浓厚的兴趣;在解决问题的过程中,指导和引导学生突出重点、突破难点,提高学生分析、归纳、及抽象思维能力,达到预期的教学目标;限于学生编程能力有限,把编写程序代码的要求放在其次。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
三、教学目标 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
知识与技能: (1)了解“递归法”的基本概念、适用条件和设计步骤。 (2)能利用“递归法”设计算法、编写程序,解决具体的实际问题。 过程与方法: (1)能通过对实际问题的分析、求解,尝试归纳出利用“递归法”解决问题的使用条件和设计步骤。 (2)能对实际问题分析,判断,甄别出适合用“递归法”解决的问题,利用所学知识,解决实际问题。 (3)从简单问题出发,逐步增加难度,增强解决问题的能力。 情感态度与价值观: (1)理解递归的意义,学会将大问题分解为小问题的思想方法。 (2)在解决问题的过程中进一步培养和提升学生的分析、归纳、总结、解决问题的能力。 (3)培养学生的主动探究分析解决问题的能力。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
四、教学重点与难点 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
学习重点: 掌握递归法的适用条件(问题); 能针对具体问题找到递归出口、总结归纳出递归函数关系式。 学习难点: 正确高效的应用递归法分析、解决实际问题。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
五、教学策略 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
情境教学法、分组讨论法、任务驱动法 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
六、教学环境及资源准备 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
教学环境: 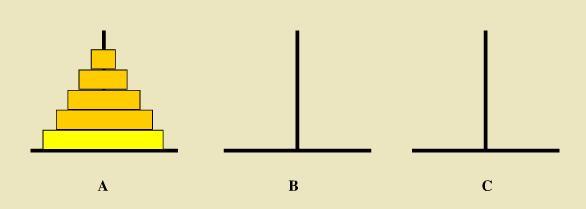 多媒体机房、因特网 教学资源: 课件、电子档案袋 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
七、教学过程(可以用嵌套表格呈现具体内容) | |||||||||||||||||||||||||||||||||||||||||||||||||||||
教学环节(第1学时) | 教师活动 | 学生活动 | 用时 | ||||||||||||||||||||||||||||||||||||||||||||||||||
新课导入 | 大屏幕展示一段视频:(问题1)有5个人坐在一起,问第5个人多少岁?他说比第4个人大2岁。问第4个人岁数,他说比第3个人大2岁。问第3个人,又说比第2个人大2岁。问第2个人,说比第1个人大2岁。最后问第1个人,他说是10岁。请问第5个人多大? (设计意图:利用学生的心理特性,激发学习兴趣,引出递归的概念,导入新课。) | 请同学简单描述求解过程。 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||
问题分析 | 引导学生回答问题 (1)递归必须有终止条件,终止条件是什么? (2)列出问题1的递归关系式,age(n)函数如何定义? (3)举例说明,哪些实际问题适合使用递归方法解决? | 回答老师问题 (1)终止条件age(1)=10 (2)函数为: 10n=1 age(n)= age(n-1)+2 n>1 (3)求阶乘问题、猴子吃桃问题等。 | 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||
算法设计 | 递归调用过程可以分为:先不断调用(回推),再依次退回(递推)。 上述递归调用过程表示如下: | 学生在word中画出函数的调用过程图,将其存储到电子档案袋中: | 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||
编程实现 | 巡视教室,指导学生写出正确的程序,具体代码如下: Public class ages { Static int age(int n) { if(n==1) Return 10; Else Return n+2 } Public static void main(String args[]) { System.out.println(“age(5)=”+age(5);) } } | 学生尝试写出程序代码,不断的修改,调试,直到运行无误,将其存入电子档案袋“我的作品”中,并以定稿形式发布。(参照课本129页,阶乘程序代码) | 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||
任务扩展 | 布置任务,教材第133页“实践与思考”第1题 教师给予指导。 | 自主分析,确定递归函数关系式和递归出口,试着写出程序。 | 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||
讨论、总结 | 1.学生通过分组讨论,回答下列问题: (1)符合什么条件的问题,适合使用递归法解决? (2)递归算法的设计步骤分为四个步骤? 2.教师对学生回答,给予归纳、总结。 | 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||
教学环节(第2学时) | 教师活动 | 学生活动 | 用时 | ||||||||||||||||||||||||||||||||||||||||||||||||||
温故知新 | 通过任务,回顾上节课知识: (问题2)斐波纳契(Fibonacci)函数问题。有一对兔子,从出生后第3个月起每个月都生一对兔子。小兔子长到第3个月后每个月又生一对兔子。假设所有兔子都不死,问第20个月兔子的总数是多少? 学生填表,回答问题,教师巡查指导(见“关键环节提炼”) | 自主分析,完成下列问题: (1)归纳出递归函数 (2)确定递归出口 (3)填写程序(关键环节提炼) | 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||
提出问题 | 大屏幕展示梵塔图片,教师讲述梵塔故事的来历,以此引入新课。 (设计意图:利用学生的心理特性,激发学习兴趣,引导学生自己动手解决问题,并帮助他们分析问题、归纳问题。) | 在网上搜索梵塔游戏fanta.exe,自己动手,体会梵塔问题,尝试解决问题。 | 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||
问题分析 | 教师提出问题: 1.盘子移动过程中的两个要求? 2.寻找规律:(教师引导,学生描述移动过程) (1)两个盘子怎么移动? (2)N 个盘子怎么移动?(可将上面的n-1个盘子“捆”在一起当作一个小盘) (3)通过(2)步操作,将n个盘子的移动简化为n-1个盘子的移动,这样如此下去,每次减少一个盘子,直到只剩一个盘子为止。 | 学生回答: 1.(1)每次只能移动一个盘 (2)一个柱子上不能大盘放到下盘下。 2.(1)move(2,a,b,c)分三步: 1号盘从a移至b move 1:a→b 2号盘从a移至c move 1:a→c 1号盘从b移至c move 1:b→c (2)可以描述为: move(n-1,a,c,b) n : a→c move(n-1,b,a,c) | 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||
算法描述 | 师生共同完成算法描述:(难度较大) 递归的边界是无盘可移,即n=0。其移动过程的算法可描述如下: Move(n,a,b,c) ①if n=0 推出程序 ②调用move(n-1,a,c,b) ③输出“盘号 柱号→柱号” ④调用 move(n-1,b,a,c) | 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||
编程实现 | 师生共同完成程序编写: 上述描述写成Java代码: //利用递归定义move()方法 Staticvoid move(int n,Sring a,String b,String c) { If(n!=0) { Move(n-1,a,c,b); //将n-1个盘从a经c移至b System.out.println(n+”: ”+a+”→”+c); //输出移动过程:将n号盘从a移至c K=k+1; Move(n-1,b,a,c); } } 完整程序,参照课本132页。 | 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||
教师总结 | 使用递归算法可以方便的解决很多实际问题,当遇到复杂问题时,我们可以通过判断问题是否能分解为若干相同性质的小问题和是否有明确的结束条件来判断是否适合用递归法来解决问题。 熟练掌握递归法解决问题的关键,在于能否准确从问题中提炼出递归函数关系式和找到递归出口。 通过本节课的学习,我们要学会把复杂的问题简单、抽象,建构合理的递归函数解决我们日常生活的实际问题。 | 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||
八、关键环节提炼 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
1.问题分析(年龄问题) 通过师生互动,明确递归调用必须要有递归结束条件(递归出口),通过学生自己总结递归函数关系式,提高学生分析问题,解决问题能力,进而掌握适合递归方法解决问题的两个条件,实现教学重点的突破。 2.温故知新(斐波纳契函数/兔子繁殖问题) 不满一个月的为小兔子,满一个月不满两个月的为中兔子,满3个月以上的为老兔子
通过问题分析,归纳递归函数表达式,进一步培养和提升学生的分析、归纳、总结、解决问题的能力,使学生掌握正确的应用递归法分析、解决实际问题的能力,实现教学难点的突破。 Public class Fibonacci { Static int fib(int n) { if(n<=2) ① ; Else ② ; } Public static void main(String args[]) { System.out. println(“fib(20)=”+fib(20);) } } 限于我校学生编程水平有限,所以通过填写程序来温习上节课学习重点,即递归出口和递归关系表达式。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
九、教学反思 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
本节内容通过探讨一些生活中的具体问题解决方法(年龄问题、兔子繁殖问题),使学生比较轻松的接受了递归算法的概念,进一步理解了递归算法的使用条件,知道递归算法的设计步骤;能够对提出的问题进行分析判断,是否适合使用递归法来解决,并能从中归纳总结出递归函数关系式、找到递归出口。本节课通过教师讲授、师生互动、学生分组讨论,充分调动了学生主动探索学习的积极性,能主动地与他人进行合作、交流,形成了一种和谐、积极参与的教学气氛。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 爱华网
爱华网



