图三中,由虚短知:V-=V+=0……a
由虚断及基尔霍夫定律知,通过R2与R1的电流之和等于通过R3的电流,
故(V1–V-)/R1+(V2–V-)/R2=(Vout–V-)/R3……b
代入a式,b式变为V1/R1+V2/R2=Vout/R3
如果取R1=R2=R3,则上式变为Vout=V1+V2,这就是传说中的加法器了。=======================================================================================
请看图四。因为虚断,运放同向端没有电流流过,则流过R1和R2的电流相等,同理流过R4和R3的电流也相等。故
(V1–V+)/R1=(V+-V2)/R2……a
(Vout–V-)/R3=V-/R4……b
由虚短知:V+=V-……c
如果R1=R2,R3=R4,则由以上式子可以推导出
V+=(V1+V2)/2
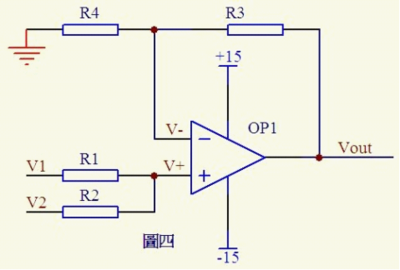
V-=Vout/2
故Vout=V1+V2
也是一 个加法器,呵呵!======================================================================================
图五由虚断知,通过R1的电流等于通过R2的电流,同理通过R4的电流等于R3的电流,故有
(V2–V+)/R1=V+/R2……a
(V1–V-)/R4=(V--Vout)/R3……b
如果R1=R2,则V+=V2/2……c
如果R3=R4,则V-=(Vout+V1)/2……d
由虚短知V+=V-……e
所以Vout=V2-V1 这就是传说中的减法器了
图13-32是运算放大器组成的加法器。两个输入信号U1、U2加到反相输入端,加法放大器将交流信号或直流信号相加,输出信号是两个输入信号的反相和。
在图13-32中,假设所有电阻都是10kΩ,U1是1V,U2是3V。输出是:
输出电压是负的,因为是在反相端求和。
改变图13-32电路,以改变输入信号的比例。例如,能够把R1变到2kΩ,输出电压是:
图13-32能够扩展成多个输入端求和。通过选择输入电阻和反馈电阻的阻值,可以改变某些或所有的输入信号在输出信号中的比例。
加法运算放大器也叫做混合器。一个音频混合器能够在录音期间,把四个麦克风的输出信号相加。反相混合器的一个优点是输入信号之间相互不影响。反相输入端是虚地端,它使一个输入信号不受其他输入信号的影响。
图13-33虚地点把一个输入信号与其他输入信号隔离开来。
运算放大器也能组成减法器。图13-34显示了可提供两个输入信号相减的电路。电路工作过程是:
U+=R3U2/(R2+R3)(1)
U-=U+(2)
Uout=U――RFI(3)
I=(U1-U-)/R1(4)
将(1)(2)(4)各式代入(3)我们得到:
如所有电阻相等,则Uout=U2-U1,输出信号是两输入信号之差。如U1=1V 、U2=6V那么:
Uout= U2-Ul= 6V -1V = 5V
如果加到反相端的电压比加到同相端的电压大,可能输出负信号。通过改变图13-34的R1或R2可以校正输入信号在输出信号中的比例。
 爱华网
爱华网