负数的补码的一种证明方法
叶 嘉 黄珍生
(广西广播电视大学理工学院 广西南宁 5--30022)
[摘要]本文首先介绍了负数补码和反码的定义,并用例子验证定义的正确性,然后从负数补码、反码的定义出发,给出了负数的补码等于该负数的反码与末位加1之和这一命题的一种证明方法与验证。
[关键词]补码;反码;证明
[中图分类号]TP311.1 [文献标识码]A [文章编号]1008-7656(2005)03-0065-02
任意一个二进制数真值在计算机中用机器数来表示,最基本的机器数有三种,即原码、补码和反码。[1]在计算机的运算过程中,根据不同的运算运用不同的机器数,可以简化计算机运算过程并很快得到运算结果。如乘法和除法用原码参与运算比较方便,符号位通过异或运算即得结果的符号位;而加法与减法运算用补码参与运算比较方便,它使符号位不用单独处理,可以一起参与运算。在计算机中,三种机器数能方便、容易地进行转换,这给使用带来极大方便。其转换要点有三:
(1)将一个数的二进制真值的最高位置上符号位(正数用0,负数用1表示),就是这个数的原码。
(2)对于一个正数,其原码、补码、反码在计算机中的表示代码相同,其代码不用改变。
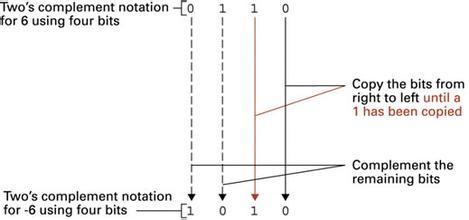
(3)对于一个负数,将原码的符号位(即二进制数的最高位,也即原码最左边的那一位)保持不变,数值位逐位取反(变为反码),末位(即最右边的那一位)加1,即得补码。也就是说,一个负数的补码等于该负数的反码与末位加1之和。[1]
本文要讨论的问题即第三个要点。这一要点在许多计算机原理的教材中使用,但很少见到这一命题的完整推导或证明过程,这给学生在学习本章节内容时只能被动地接受命题,不了解例题的理论依据。因此,教师在教学中适当地从理论的高度论述原码、补码和反码之间的转换关系很有必要。本文从补码、反码的定义出发,给出这一命题的简单证明,与同行分享与讨论。
一、对于定点负整数
(一)、补码的定义[2]如下:
[X]补=2n+XMOD(2n)(1)
从定义知,一个n位二进制定点负整数,求其补码时,用2n为模数加上该负数即可。
例如:已知n=8,X=-1010101,则
[X]补=2n+X=28+(-1010101)
=100000000-1010101
=10101011
(说明:28的二进制为100000000,简记:28的二进制为1个1后有8个0)
(二)、反码的定义[2]如下:
[X]反=(2n-1)+X[MOD(2n-1)]……(2)
从定义知,一个n位定点负整数,求其反码时,用2n-1为模数加上该负数即可。
例如:已知n=8,X=-1010101,则
[X]反=(2n-1)+X=(28-1)+(-1010101)
=11111111-1010101=10101010。
有了以上定点负整数补码,反码的定义,我们就很容易地证明,对于任一定点负整数,其补码等于其反码末位加1。
由(2)式,[X]反=(2n-1)+X,得:
X=[X]反-2n+1
将其代入(1)式,有
[X]补=2n+X
=2n+[X]反-2n+1
=[X]反+1(A)
根据以上推导,命题对于定点负整数是成立的。
二、对于定点负小数
(一)、补码的定义[2]如下:
[X]补=2+XMOD(2)(3)
从定义知,一个n位二进制定点负小数,求其补码时,用2为模数加上该负数即可。
例如:已知n=8,X=-0.1010101,则
[X]补=2+X=2+(-0.1010101)
=10-0.1010101
=10.0000000-0.10101011
=1.0101011
(说明:2的二进制为10,写成小数即10.000000[3])
(二)、反码的定义[2]如下:
[X]反=2-2-(n-1)+X[MOD(2-2-(n-1)](4)
从定义知,一个n位定点负小数,求其反码时,用2-2-(n-1))为模数加上该负数即可。
例如:已知n=8,X=-0.1010101,则
[X]反=2-2-(n-1)+X
=2-2-7+(-0.1010101)
=10-0.0000001-0.1010101
=1.1111111-0.1010101
=1.0101010。
(说明:2-7的二进制为0.0000001,简记为:2-7的二进制为小数点后第7位为1,其余位为0。(小数点后第7位即为8位二进制负小数的最末最右的一位)[3]
同理,有了以上定点负小数补码,反码的定义,我们也能很容易地证明,对于任一定点负小数[4],其补码等于其反码末位加1。
由(4)式,[X]反=2-2-(n-1)+X,得:
X=[X]反-2+2-(n-1)
将其代入(3)式,有
[X]补=2+X
=2+[X]反-2+2-(n-1)
=[X]反+2-(n-1)(B)
上式中,2-(n-1)的二进制即为小数点后第n-1位为1,其余位为0,小数点后第n-1位为1,即n位定点小数最右最末的一位为1[4]。因此上式:[X]补=[X]反+2-(n-1),也就是X的补码等于其反码与末位加1之和)
根据以上推导,命题对于定点负小数同样是成立的。
综合(A)式和(B)式,可得我们要推导证明的命题成立。
[参考文献]
[1]俸远祯.计算机组成原理与汇编语言程序设计[M].北京:中央广播电视大学出版社,2001:3.
[2]李明慧.计算机组成原理[M].北京:中央广播电视大学出版社,1997:10.
[3]白中英,韩兆轩.计算机组成原理教程[M].北京:科学出版社,1988.
[4]侯炳辉.计算机原理[M].北京:经济科学出版社,2000.
[作者简介]叶嘉,女,广西广播电视大学理工学院讲师。黄珍生,男,广西民族学院计算机与信息科学学院讲师,信息管理与信息系统教研室主任。
 爱华网
爱华网