《折线统计图》
安徽省淮北市黎苑小学 韩东
知识背景和目标定位:
《折线统计图》是义务教育课程标准实验教科书(人教版)四年级下册的内容,它是在学生已经掌握了收集、整理、描述、分析数据的基本方法,会用统计表(单式和复式)和条形统计图(单式和复式)来表示统计结果,并能根据统计图表解决简单的实际问题;了解了统计在现实生活中的意义和作用,建立了统计的观念的基础上,又一次认识一种新的统计图。
基于以上认识,把《折线统计图》的教学目标定位于以下几点:
1、认识折线统计图,并知道其特征。
2、能从折线统计图中发现数学问题,同时能够依据数据变化的特征进行合理的推测。
3、通过对数据的简单分析,进一步体会统计在生活中的意义和作用。
案例描述:
一、创设情境。
1、观看科技展录像。看到这些画面,你想说点什么?
2、为了使大家能更清楚地了解和分析这几年参观科技展人数的情况,你认为可以用哪些方法来表示参观人数呢?
3、课前我已收集了近几年来参观科技馆的人数,并把它制成了这样一张统计表。仔细观察,你能从统计表中了解到什么信息?
参观科技展人数统计表 2007年4月
年份 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 |
人数(万人) | 24 | 18 | 30 | 36 | 36 | 54 | 60 |
出示问题:在相邻的两个年份中,( )年到( )年参观人数增加最快。
你怎么得到这个答案的?你是用什么方法知道的?(计算)
4、能不能不通过计算,换一种方式就可以直观得看出2004年到2005年人数增加最快呢?(条形统计图)
但是,我在科技馆发现了他们用这些数据制成了这样的一幅统计图。(课件折线统计图)
二、探究新知
1、初步感知
(1)这幅统计图中,横轴表示?纵轴表示?
(2)每年的参观人数在这幅统计图上都找到吗? 谁来指着说一说。
(3)这幅统计图是通过什么来表示出每年的参观人数的?(板书:点:数量多少)
(4)思考:目前这幅统计图也只是反映出了统计表里的信息,还不能解决刚才问题?
看来这个问题有必要我们研究研究。我们不妨带着下面三个问题来看一看。仔细观察,独立思考。然后再把你的想法在小组内说一说。
2、深入探究
(1)哪年参观人数最多?哪年最少?
(2)哪年到哪年人数没有变化?哪年到哪年人数增加最快?
分析:回到前面的问题,在统计表中想知道参观人数增加最快的是哪年到哪年,是通过什么方法得出的?那现在能直观的看出来了吗?(通过线的陡度来看)
板书:平—不变
陡—快
(3)借助这幅统计图,体会一下这几年参观人数整体变化情况。你是怎么看出的?
让学生看整条线段,感受整体趋势。
课件演示整体上升的过程。
你们是通过什么看出来的上升的趋势的?(板书:线)
总结:通过折线的起伏,来反映出数量的增减变化。这正是这种统计图的特点,不仅能够看出数量多少,而且能够更清楚地看数量的增减变化情况。(补充板书:增减变化)。
3、为统计图起名字
你知道这种统计图叫什么名字吗?让学生根据这幅统计图的特点,自由起名。(板书课题:折线统计图)
4、预测
能不能根据这幅折线统计图来猜想一下,2007年会有多少人来参观?
总结:同学们,这只是一种猜测,不管是多是少,都有可能,要想知道究竟有多少人来参观,还要年底再作一次调查。
5、感知生活中的折线统计图。
我们已经对折线统计图已经有了一定的认识,想想,生活中你还从哪儿见过折线统计图?(报纸上、股市上、父母单位、电视里……)
三、实践应用。
1、分析折线统计图
出示马鞍山师范附小四年级春季收费标准统计图,从图中你可以获得哪些信息?有什么想说的?
总结:全国在义务教育阶段,开始免收学杂费了,这项改革是真正惠及到咱们千家万户的好事、实事,使得大批因家庭经济困难辍学儿童能重返校园,是义务教育的一座新的里程碑。
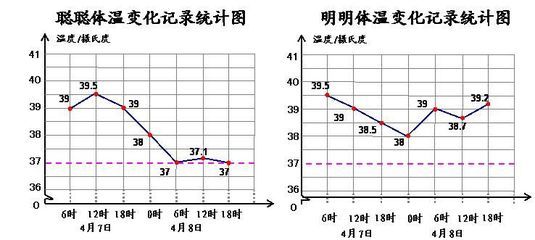
2、聪聪、明明两人患病期间体温变化的统计图
请学生当小医生,分析一下聪聪和明明体温变化情况。
3、“小华学习了折线统计图,觉得折线统计图的优点很明显,就去文具店作了调查,并绘制了一幅统计图。请你认真观察分析这幅折线统计图,你发现了什么?”(不同文具的销售情况)
(1)、让学生体会到若描述的是不同事物,则需要制条形统计图;若描述同一事物的变化趋势,则制成折线统计图。
(2)、如果想让它合理,怎么在这张统计图上作一些简单的修改?(改成条形统计图)
(3)、做完这个问题后呢,就给咱们带来了一个新的问题:在什么情况下,绘制折线统计图,在什么情况下绘制条形统计图,这个问题其实是以后要研究的内容,你们刚才的发现已经很了不起了。
四、拓展。
(课件图文并茂出示)探究我国历史,于上古时代已能看见统计图理念的身影。周易系辞记载“上古结绳而治”,事大,大结其绳,事小,小结其绳,显示已使用“分组”的观念区分大、小事,并运用实体的图像表达所观察到的事象。
到商汤推行井田制度,把地划为九块,形如井字,八家各分一块为私田,中为公田,显见井田制度已略具统计图之轮廓。
到宋代,南宋史学家郑樵的图谱思想等,则与现代统计图表的制图原则相近。
至清朝,统计图已广泛的制作与运用,包括农工商统计图、交通统计图及教育统计图等。至今,统计图已广泛用于生产生活,也演变出形式各异的统计图。除了我们已学过的条形统计图、折线统计图以外,还有柱形统计图、饼形统计图、面积统计图、雷达统计图等等。
师:孩子,大自然的千姿百态,无穷无尽的变幻,造就了无以计数的物象形态。其实在自然界中也存在天然的统计图,看(课件出示树的年轮)这不正是大自然的杰作吗?
在实践反思中提升
安徽省淮北市教育局教研室 田志锋
今年五月份,我市青年教师韩东参加了安徽省小学数学课堂教学优质课比赛,他执教的《折线统计图》(义务教育课程标准试验教科书<人教版>四年级下册)一课,给评委和听课教师留下了深刻的印象,结果获得一等奖。作为一名教研员,笔者参与了这次活动的前前后后,通过备课、研磨,经历了一段艰辛和愉悦,换来了个人和群体专业水平的提升。
一、关于情境创设
初次教学韩老师创设一天气温变化情境,出示气温变化情况条形统计图,然后提问:横轴表示什么?纵轴表示什么?从这幅图上你可以获得哪些信息?(生回答)。从这幅统计图上很直观地看出这一天不同时刻的温度,如果我们想一眼看出这一天气温的整体变化情况,该怎样画统计图?(学生沉默)。能不能发挥你想象的翅膀,在条形统计图上大胆作修改或补充?学生小组为单位交流、修改。教师提示、引导,最后引出折线统计图。
教师不拘泥教材,开发一天不同时刻气温的资源,并运用北师大版教材的处理方法。但当我们系统阅读北师大版教材并思考其编排意图时,发现北师大版教材是把条形统计图和折线统计图编排在同一单元,以条形统计图为基础,利用知识的迁移学习新知,并且都是围绕“栽蒜苗”这一情境开展活动,探究新知的,而人教版教材却是把它们分在两个学期学习的,显然这样处理是不妥的。在磨课时大家思考:学生怎能想到在条形统计图上进行修改?教师参与小组活动时是否已经暗示学生?另外统计气温这一情境,学生虽然熟悉,但不去关心它,学生的体温是自己关心的事,而且很多学生有住院治疗的经历,可否换成生病学生体温测量的情境?带着这些思考和困惑,备课组成员交流、研讨,共同改进。
再次教学时,先播放护士量体温的情境,而后出示小明体温测量情况统计表,让学生观察讨论,你能从统计表中知道什么?(学生交流、发言)。老师对同学们的发言给予表扬、鼓励,然后问:从几时到几时小明的体温增加的最快?这时学生的答案不能统一,还有的学生开始动笔计算,这时教师满足学生的需要,让学生计算。当学生忙于计算时,教师提出一个挑战性的问题:我们能不能不计算就可以直观地解决这个问题?这一问题激发了学生的兴趣,激活了学生的思维。学生经过思考,争先恐后地回答可以画统计图……教师适时出示小明体温记录折线统计图,探究新知。
这次改变教材的呈现方式,由统计表到折线统计图,提出挑战性问题,让学生感悟折线统计图的优越性,激发学生探究新知的欲望。这样顺学而导,符合学生的心理规律和认知特点,让学生在矛盾冲突中找到新方法,学习情绪高涨。当大家非常满意时,我发现苏教版教材的编排是把小数加减法放在折线统计图后,学生不能通过计算解决问题(因比赛地马鞍山四年级用的是苏教版教材),教学又一次陷入了困境。
当我们苦思而不得其所时,一次南京之行为我们提供了一个素材。在南京科技馆我们很巧合的遇到马鞍山的学生正在参观科技展(其中有上课学校的学生),于是我们用摄像机录下了这一情境,把量体温的情境换成参观科技展的情境。学生对科技展很感兴趣,又看到自己亲身经历的事,学习主动,课堂气氛非常活跃,收到意想不到的效果。
让学生在生动具体的情境中学习数学,在现实情境中体验和理解数学,这时课标倡导的新理念。教师在教学过程中应充分利用学生的生活经验,创设与学生的生活环境,知识背景密切相关的,又是学生感兴趣的学习情境,激起学生的生活体验,并自觉用数学的思维方式来解决生活中的问题。
二、关于三个问题
数学教学是数学活动的教学,是师生之间、学生之间交往互动与共同发展的生命历程。学生在课堂教学过程中,自主学习,合作交流,产生思维的碰撞,智慧的启迪,获得成功的体验,增强学好数学的信心。
教师要尽量给学生提供探索交流的空间,提出具有挑战性的问题,调动学生思维,提高教学实效。在深入探究折线统计图特点的教学中,最初是让学生观察折线统计图后,通过小组交流,指名汇报,由于比较开放,学生的思维没有一个明确的指向,所以学生说的五花八门,甚至离题万里,而且大部分学生还是用“比较相邻两个数字差”的方法比较何时上升最快,而不能根据线段的长度、“陡”度等作答,所以也就不能深刻理解折线统计图表示“增减变化”的特点。针对这一问题,后来设计了三个问题:
(1)哪年参观人数最多?哪年最少?
(2)哪年到那年人数没有变化?哪年到那年人数增加最快?
(3)借助这幅统计图,体会一下这几年参观人数整体变化情况。你是怎么看出的?
教学过程中,教师首先让学生在统计图上指点找数据,学习描点方法,并让学生体会折线统计图用点表示数量多少,而后让学生交流,说自己的发现,再出示三个问题,给学生明确思维的导向,教师再适度引导,让学生抓住折线统计图点、线的特点发现规律:折线统计图不仅能看出数量多少,还能更清楚地看出数量的增减变化,而且能对事物进行合理的判断和预测。从而培养和发展学生的统计观念。课堂教学中有师生情感的投入,闪现学生思维和智慧的火花,不时出现学生的独到见解和真知灼见。
三、关于实践应用
小学统计教学的核心目标是发展学生的统计观念,认识到统计在社会生活及科学领域中的应用,并能解决简单的实际问题。在实践应用环节,教师为学生提供了富有现实意义的素材,让学生解决生活中的问题,使统计知识与生活建立紧密的联系。最初的教学我们选用奥运会、农民收入、沙尘暴三个素材,但学生的积极性不高,教学的效果不理想,这是什么原因?
我在思考:奥运会、农民收入、沙尘暴都是当今社会倍受关注的问题,但学生关注吗?与学生的现实生活联系紧密吗?如沙尘暴对我国东部学生来说,只是在电视、报纸上看过,有深刻体会吗?奥运会虽是家喻户晓,但不能充分体现折线统计图的优势。后来备课组认真讨论,集体研磨,又求教小学数学专家,决定把三道实践应用题改为:义务教育阶段学生学费问题,在应用新知解决问题的过程中使学生感受到国家对教育的重视,对少年儿童的切身关怀;看聪聪、明明两人生病时的体温统计图,让学生判断谁病情好转了;统计文具店一月中卖出不同文具的问题,让学生通过辩论后感悟用折线统计图不合理,最后经过讨论后学生认为用条形统计图比较合理。这样的素材是发生在学生身边的,贴近学生生活的,学生比较感兴趣的,能激起学生的学习欲望,收到预期效果。
比赛结束了,但我的思考没有结束:参观科技馆的情境学生熟悉,但统计参观人数这样的统计表离学生是远的,“万人”更远,有更好的情境吗?探究折线统计图时,非要从学生嘴里抠出“陡”度,流失了很长时间,有这样的必要吗?这样对学生的牵引迹象是不是太重?本来安排向学生介绍“折线统计图的发展史”,对学生进行数学文化的渗透,而因时间关系未能介绍,遗憾吗?
边走边停边回望
——对“指向性问题”的探讨
安徽省淮北市黎苑小学 韩东
边走边停:
这是在《教学大纲》时代设计的一课片断:
出示:比较3/4和5/6的大小。
师:怎样比较这两个分数的大小呢?请你们带着下面三个问题想一想,然后再小组内说一说。
(1)这题和我们以前学习的分数比较大小有什么不同的地方?
(2)怎样用我们以前学过的知识来解决这个问题呢?
(3)什么叫通分?
……
这是五年级《通分》一课的片断,还记得以前的课经常用到这种指向鲜明的问题,来引导学生的思维,使学生能心无旁骛的投入到所学的知识点上。正是这种主题明确的问题,使学生的思维不会偏离所教的知识点,总是很好的围绕着这几个浓缩性很强的问题来研究讨论。这种方法的一个最大优点就是教学层次鲜明,井然有序,扎实高效。
从2001年开始,全国上下轰轰烈烈地进行了一次意义重大、影响深远的新课程改革实验。新的教育理念,新的教育思想,新的教育方法给教师们的心灵带来巨大的冲击,一时间课堂和学生学习出现了巨大的变化,新型的课堂氛围迅雷不及掩耳地形成,呈现出了一派繁荣的景象。于是,我们开始对以前教学总喜欢提出明确问题,让学生就几个问题展开学习提出了质疑:这样做有利于学生的创新思维吗?会不会禁锢学生天真独到的想法?这时像跟风似的一些新的教法出现了:
片断一(通分):
出示:比较3/4和5/6的大小。
师:你能想办法来比较这两个分数的大小吗?把你的想法和小组内的同学说一说。
……
片断二(小数的初步认识):
播放超市购物的录像,里面有很多超市的商品价格。
师:看到以上画面,你了解到了哪些信息?
生:我看到了我最爱吃的××。
生:里面还有变形金钢呢。真好看,真想买一个回家玩。
生:老师,我知道这是哪儿。这是我们“亿家人”超市,星期天妈妈还带我去那买东西呢
……
对于片断一的教学,比以前更开放了,学生的思维也更活跃了,随之而来的想法也更多了。学生能从多视角、多维度、全方位地理解和学习知识,在开放的情境中不断地有所发现、有所创造、有所前进。而片断二更是让学生充分发挥自己的观察表达能力,学生不断地有新的发现,他们的情绪也不断地高涨。
课改进行了一两年后,这种盲目追风、人云亦云的“空泛性问题”逐渐被人们所批判,这时我们的脚步又慢慢停了下来,开始了一定程度上的反思。“你了解到了哪些信息?”类似于这样的话,在我们的数学课堂中有什么用呢?学生对于一些非数学信息的表达,只会浪费课堂宝贵的时间,根本就无利于数学思维的发展。于是新的探索又开始了。为了兼顾课改开放思想与数学思维发展,我们又想到了一句比较“完美”的话:“你了解到了哪些数学信息?”虽然只是加了“数学”两个字,却是和前者有着很大的差异。“信息”包罗万象,而“数学信息”则圈定了学生的思考范围。因此上面片断二的教学就会出现以下情节:
片断二(小数的初步认识):
播放超市购物的录像,里面有很多超市的商品价格。
师:看到以上画面,你了解到了哪些数学信息?
生:我知道了××的价格。
生:我知道了××比××要贵得多。
生:我知道了××和××两种在一起都没有××贵。
生:我看到了里面有很多小数。
……
瞧,加上“数学”两个字,就是不一样吧,学生的思维不再是漫无边际了,他们已能围绕着数学知识在观察思考,数学味变得越来越浓了,所以时下,这种方法依然受到大家的推崇与应用。
思考与回望:
课改在历经检验的过程中一步步地前进,我们在教学过程中也在静静地思考。从之前的提出“指向性问题”到提出“空泛性问题”,我们的思维开始出现了两种观点的碰撞:一种观点认为不要提出指向明确的要求,这样会约束学生的思维空间;另一种观点认为一定要提出指向明确的要求,知识的提升来源于有效的引领。
于是我有针对性地进行了实验,下面是《折线统计图》中的片断(基于“空泛性问题”的设计):
师:同学们,目前看来这幅统计图也只是反映出了统计表里的信息,还是不能解决刚才的问题?(不通过计算,换一种方式就可以直观地看出2004年到2005年人数增加最快)
让学生想一想后,师:看来这个问题有必要我们研究研究。仔细观察这幅统计图,看看你能发现些什么?然后把你的发现在小组内说一说。
生1:我发现这里面有很多网格。
生2:我知道为什么要有网格,因为这样更好地找点。
生3:我发现了这幅统计图把点用线连起来了。
师:那这些线有什么用处呢?
生3:可能是为了美观吧。
生4:我不同意,我认为用线连起来可以看出参观人数在上升。
师:是吗?能具体说一说吗?
生4:如果线升了,就表明人数在增加,下降了就表明人数在减少。
师:了不起的发现!那你认为从整体上看,这几年的参观人数是怎样变化的?
生4:有下降,也有上升的。
师:你是一段段看的,从整体上看呢?还有别的意见吗?
生5:上升的多,下降的少。
师:那也就是从整体上看是上升的。你们还有什么发现吗?
生6:我发现这种统计图很好玩,就像一个“之”字。
生7:这种统计图不要标数字就可能看出参观人数。
……
在这个片断中,不难发现学生在思考交流时,虽然提出“看看你能发现些什么?”这一问题,但学生思考交流盲目、泛泛而谈,东一榔头,西一棒槌,没有一个明确的方向。这种“答案的丰富多彩”掩盖了对折线统计图特点的探讨,虽有部分学生提出了“线的变化反映人数的变化”,但这毕竟只是部分,而另一部分学生只是在交流中白白浪费时间。学生的思考交流要凸显数学知识的本质属性,要能够从问题中有效的引出数学知识,不要让他们雾里看花般讨论了老半天还没有什么所以然。这时我想到了《教学大纲》时代的教学方式,可不可以在思考交流前提出明确要求,引领学生有序思考?
下面是《折线统计图》中的片断(基于“指向性问题”的设计):
同学们,目前看来这幅统计图也只是反映出了统计表里的信息,还是不能解决刚才的问题?(不通过计算,换一种方式就可以直观得看出2004年到2005年人数增加最快)
让学生想一想后,师:看来这个问题有必要研究研究。我们不妨带着这三个问题来看一看,(课件出示)仔细观察,独立思考,然后把你的想法在小组内说一说。
(1)哪年参观人数最多?哪年最少?
(2)哪年到哪年人数没有变化?哪年到哪年人数增加最快?
(3)借助这幅统计图,体会一下这几年参观人数整体变化情况。你是怎么看出的?
有了这三个问题,学生的独立思考、自主探究、合作交流有了有效的平台,面对问题,学生大多能够凭借思考交流,顺利发现折线统计图的另一个优点:通过折线的变化,来反映出数量的增减变化。通过这两者的对比,不难发现在探讨折线统计图的特点时,如果没有明确的问题导向,学生的思维虽然能展开,但有可能造成喧宾夺主的结局。
由此我认为指向性问题,在我们数学课中很有必要,它和课改的思想,理念没有冲突,所以我们不应该惧怕它,厌恶它,认为它已过时,其实只要你用得合理,用得适度,必将会为数学课堂增添针对性和实效性。
当思考到这儿时,不禁又产生了一个新问题:什么时候运用“指向性问题”合理?怎样设计“指向性问题”才叫适度?“指向性问题”和“空泛性问题”的融合点在哪里?这些问题必将成为我以后思考、探讨和实践的方向。
有无相生:课之佳境
——观摩韩东老师《折线统计图》一课后有感
北京第二实验小学 华应龙
欣赏完韩东老师的《折线统计图》,我的脑子里一下子冒出了老子的话语:“有无相生”、“众妙之门”。再三回味,还是觉得:一节好课妙就妙在这四个字——“有无相生”。
《老子》中专门讨论“有”“无”问题的有十四章之多,“有”“无”的含义又极为丰富。“无,名天地之始。有,名万物之母。故常无,欲以观其妙。常有,欲以观其。此两者,同出而异名,同谓之玄。玄之又玄,众妙之门。”本无是天地的原始,妙有是万物万有的来源。人们要想体认大道有无之际,必须要修行到常无的境界,才能观察到有生于无的妙用。冯友兰先生说:“《老子》所说的‘道’,是‘有’与‘无’的统一。”“道”既是“无”又是“有”。用“无”来称呼“道”,是因为它不是被别的东西生出来的,是本来就有的,是初始的;用“有”来称呼“道”,是因为它具有生出天地万物的能力,可以把“有”解释成“制造出来的”更好懂。南怀瑾先生说:“这个有无互为生灭的观念,从周末而到现代,几千年来,一直成为中国文化中普遍平民化的哲学思想。”
从经验来讲,天地万物的从有还无,是很自然的事实。但是要说万物的有,是从无中生出,实在是一件不可思议的事情。东西方数千年的哲学,也没有一个明确的结论。在此,我只是借话说话。
韩东老师为什么能把一般老师不敢上、不愿上的一节数学课上得如此动人?如此深入人心?
我想是因为——无中生有。
他课中所设情境的“有”,在我们头脑中“无”,又是生活中本来就有的,是老子所说的“无”,因此我们觉得玄妙无比。
南京科技馆的话题切入,激活生活,调动已知,引领探究,一石三鸟。不过,令人惊奇的是——淮北的老师要到马鞍山借班上课比赛,上课前去南京科技馆正好遇上马鞍山的孩子来参观。真是巧合,几个小概率事件竟然在韩东一个人身上都变成了现实。真是“文章本天成,妙手偶得之”?只有自己心中有,眼中才会有吧?
“马鞍山师范附小四年级春季收费标准统计”情境具有现实意义。话题的讨论,更有教育意义。当代的孩子享受了太多的爱,但是他们往往感受不到,更不会表达和回报。
上这样的课,老师们都会想到医院的体温记录表,但韩老师一下子出示两幅图:“聪聪、明明的体温变化记录统计图”,让学生当一名小医生仔细观察分析这两幅图,给大家详细地说说这两天他俩的治疗情况,有情有趣,有理有据。
回顾全课,由学生头脑中没有折线统计图,到创造出来;由一幅到两幅,再到学生举例的多幅。哈哈,一幅完美的“道生一,一生二,二生三,三生万物”的演绎图景。
在小结全课之后,韩东老师使出一招漂亮的回马枪:“小华学习了折线统计图,觉得折线统计图的优点很明显,就去文具店作了调查,并绘制了一幅统计图。请你认真观察分析这幅折线统计图,你发现了什么?”“你发现了什么?”是开放度很大的问题,有的孩子可能不明就里,但培养的是学生的独立思考,敢于批判,不人云亦云。
我惊叹这一反例!这一反例在生活中是没有的,是一种“无”,但无中生出了“有”,促使学生深刻地认识到“在什么情况下,绘制折线统计图,在什么情况下绘制条形统计图”,真是相反相成,精妙独到!
韩东老师为什么能把一般老师不敢上、不愿上的一节数学课上得如此动人?如此深入人心?
我想是因为——有中生无。
毫无疑问,对这节课韩老师是精心预设的,但他上得没有斧凿的痕迹,水到渠成,一气呵成,叹为观止。师生之间的圆融,让我想到庄子的“鱼相忘乎江湖,人相忘乎道术。”这种消除了主客对立的“相忘”境界,“无我”“浑沌”状态,我以为是课堂教学的至高境界。
我们可以一起回顾他在学生回答、展示后的评价语——“瞧!他关注了什么?”“多了不起的发现!”“哎!这回说得更专业了。你说倾斜度,什么是倾斜度,能比划比划吗?”“真好!提出挑战了,我最喜欢这样的课堂,有争议才有进步吗!听到他质疑,你们作何解释?”……丰富多彩,准确灵动。语言的丰富正由于理解的准确,认识的到位。我想这是“有中生无”。
《老子》说“有之以为利,无之以为用。”它的意思是说:“有”给人便利,“无”发挥了它的作用。我们写出的教案是“有”,它让我们更好地把握课的走向,我们实际用的是教案字里行间的“无”。
不过,看上去的“无”,其实还是老师心中“有”。老子说:“天下万物生于有,有生于无。”请看在分析“聪聪、明明的体温变化记录统计图”时——
生3:她分析得很好,但我会比他分析得更好。
师:那么自信,你贵姓?(姓胡)胡医生,可不要胡说哟!我们可要听听你精彩分析。
……
我猜想韩东老师心中是有著名作家、翻译家胡愈之到大学讲课时开场的故事的。“我姓胡,虽然写过一些书,但都是胡写;出版过不少书,那是胡出;至于翻译的外国书,更是胡翻。”我没有看到孩子的眼睛,韩老师可以回忆一下,当自己说“胡医生,可不要胡说哟!”胡姓学生的目光有何变化。自己说自己“胡说”,那是一种调侃,别人说呢?
有无相生,生生不已。一切作为,如行云流水,义所当为,理所应为,做应当做的事。做过了,如雁过长空,风来竹面,不着丝毫痕迹。
韩东老师的课后反思也很见功力。“学习素材无处不在,也取之不尽,用之不竭。只要我们关注学生,关注他们的生活现实,关注身边的大事,小事,必然会使数学“材”源茂盛,使课堂焕发魅力。”说得真好!只有“风声雨声读书声声声入耳,家事国事天下事事事关心”,才能找到恰当的、学生喜闻乐见的、既有数学味道又富有思想含量的例子,找到“这一个”。你见青山多妩媚,料青山见你亦如是。著名数学教育家波利亚曾形象地说:“好问题同某种磨菇有些相像,它们都成堆地生长,找到一个以后,你应当在周围找一找,很可能附近就有好几个。”韩老师的反思可以启发我们更多的思考,我相信我们会有所得。
我觉得反思应该是“道通天地有形外,思入风云变幻中”的形而上学,应该“有中生无”,从课中的“有”,反思出课中没有觉察的问题。因为反思主要是为了发现问题,分析问题,解决问题,提高自己。教是修行,思是觉悟。在思想光芒照耀下的课堂更有利于学生成长。
比方说——
在“探究新知”环节,老师出示参观科技展人数统计图后问:“在这幅统计图中,横轴表示什么?(年份)纵轴表示什么?(参观人数)每年的参观人数在这幅统计图上都找到吗?”韩老师是不是可以反思一下:前两个问题需要老师提出来吗?这两个问题可是看懂统计图的关键啊,看不懂统计图的学生往往就是不知道先看懂横轴、纵轴分别表示什么。这一关键能不能让学生自己体悟出来?还可以再问自己一句:这两个问题老师不说,学生会想到吗?学生有没有相关基础?条形统计图是基础,这在“知识背景和目标定位”已经分析了的,那这么做又是为什么呢?赶时间?图效率?在教学的关键环节,我们是不是应该“舍得浪费时间”(卢梭语)呢?
同样,在“深入探究”环节的三个问题:
(1)哪年参观人数最多?哪年最少?
(2)哪年到哪年人数没有变化?哪年到哪年人数增加最快?
(3)借助这幅统计图,体会一下这几年参观人数整体变化情况。你是怎么看出的?
是不是也可以反思:问题是数学的心脏,这三个问题来自哪里?是来自学生,来自老师,还是来自教参,来自以往的教学习惯?
我似乎听到老子在说:“无可无不可。”
哈哈,以老子看来,应当是“知者不言,言者不知”,我不敢乱说了。
资料来源:http://eblog.cersp.com/userlog18/39577/archives/2008/899197.shtml
 爱华网
爱华网