把反例演绎得更精彩
| 来源: 作者:叶天荣 |
题目1:体积相等的两个长方体表面积也一定相等。题目2:表面积相等的两个长方体体积也一定相等。请判断上述的说法对吗?如果认为是错误的,请举出反例,并归纳出举反例的一般方法。
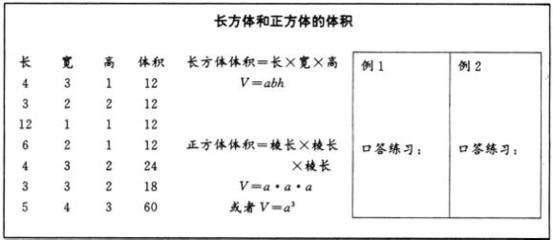
题目1的说法是错误的,即体积相等的两个长方体表面积不一定相等,譬如说一个长方体的长、宽、高分别是4、3、2厘米,那么它的体积是4×3×2=24立方厘米,表面积是(4×3+4×2+2×3)×2=26×2=52平方厘米,另一个和它体积相等的长方体的体积24立方厘米可以分解成长、宽、高分别是2、2、6厘米,这时它的表面积却是28×2=56平方厘米。当然长、宽、高也可以是8、3、1厘米,但它的表面积却是35×2=70平方厘米。由此可见体积相等的两个长方体表面积不一定相等。举反例的一般方法是将体积分解成三个因数相乘的形式,就可以得到长、宽、高的长度分别是多少。上述反例仅在整数范畴内,如扩大到小数、分数范畴,可以说它有无数组长、宽、高。
题目2的说法也是错误的,但举此反例就没有上述情况简单,所举数据凑巧可以出现;如果不凑巧,那么还真难找呢?所以一定要归纳出举反例的一般方法,可以避免无目的的乱凑。
根据需要我们将长方体分成二种类型:一种是二个面是正方形,另四个面是长方形的长方体,另一种是六个面都是长方形的长方体。
一个长方体的长、宽、高分别是4、4、8厘米,这时它的底面是正方形,表面积是80×2=160平方厘米,体积是4×4×8=128立方厘米。举反例时另一个长方体的表面积也应是160平方厘米,而它的体积由另一组长、宽、高而定,我们任意假设它的长=宽=8厘米,则它的底面积是8×8=64平方厘米,长方体的前面与右面面积之和是160÷2-64=16平方厘米,因为长=宽=8厘米,前、右面面积又相等,所以前面面积=16÷2=8平方厘米,高=8÷8=1厘米,即长、宽、高分别为8、8、1厘米,此时的表面积仍是80×2=160平方厘米,而体积却是8×8×1=64立方厘米。
归纳为一般方法为:(表面积的一半-底面积)÷2÷长=高
当长、宽、高分别是8、6、4厘米时,这时长方体的六个面都是长方形,它的体积是8×6×4=192立方厘米,表面积是104×2=208平方厘米。举反例时另一个长方体的表面积也看作208平方厘米,它的体积则应由另一组长、宽、高而定。我们任意假设长与宽分 别为10、2厘米,那么底面积为10×2=20平方厘米,而前面和右面面积之和为104-20=84平方厘米,所以高=84÷(10+2)=7厘米,这时的体积为10×2×7=140立方厘米。
上述的结果是开放的,它的结果不是唯一的,长、宽、高可能是整数,也可能是小数,甚至是分数,但无论怎样,表面积相等的两个长方体的体积就是不一定相等,归纳举反例的一般方法为:(表面积的一半-长×宽)÷(长+宽)=高,利用这种方法就可以求出表面积一定时长、宽、高另一种情况的反例。
事实上长方体中的底面是正方形属特例,也可以纳入六个面都是长方形的情况之中,所以归纳二种方法也可以统一为后一种方法即:(表面积的一半-长×宽)÷(长+宽)=高。
 爱华网
爱华网