毕达哥拉斯与勾股定理
毕达哥拉斯像
【注】1951年《中国数学》杂志将“毕达哥拉斯定理”以“勾股定理”命名
古希腊的毕达哥拉斯定理
古希腊所在的地域并不仅限于现在的希腊,还包括塞浦路斯,土耳其的爱琴海海岸,意大利的西西里岛等很多地区。传统上,古希腊所指的时间从公元前776 年的第一届奥运会开始,到公元前 146 年并入古罗马帝国结束。
古希腊的科技和文艺达到了极高的水平。那时的科学家就已经知道地球是圆的,绕着太阳转,而且还精确的测量了赤道的周长。许多伟大的科学思想都可以追溯到古希腊,例如物质是由原子构成的,生物是进化的等等。
古希腊的数学当然也是非常发达的。欧几里德的《几何原本》是一个光辉的顶峰,在长达两千多年的时间里,一直是世界各国的标准教科书。《几何原本》第一册的第47个命题就是勾股定理,书中给出了严格的,真正的数学意义上的证明。这个证明和勾股定理的证明类似。《几何原本》原文不是说多边形,而是说图形。这当然是正确的,即使是对歪歪扭扭,弯弯曲曲的图形,这个结论也是完全正确的。但是欧几里德在证明的时候是按照多边形来证明的,所以我们在这里写成多边形。
西方认为是毕达哥拉斯最先证明勾股定理,所以称其为毕达哥拉斯定理。其实并没有确凿的证据能说明是毕达哥拉斯证明了这个定理,甚至都没有证据证明是毕达哥拉斯发现这个定理的。
大约公元前569年,毕达哥拉斯出生于爱奥尼亚的萨摩斯岛。爱奥尼亚是古代小亚细亚西部沿爱琴海海岸的一个地区,当时是古希腊的殖民地。那个时候的爱奥尼亚科技水平很高。其后由于宗教势力的影响,爱奥尼亚的科学传统没有能保留下来。整个世界一直等到两千年后的文艺复兴,科技方面才赶上爱奥尼亚当年的水平。
在古希腊文献里面最早提到毕达哥拉斯跟几何有关系的是普路塔克。他是公元一世纪的古希腊作家和哲学家。
普路塔克说毕达哥拉斯因为发现了一个重要的几何定理,杀了一头公牛来献祭。但是普路塔克不能肯定这个几何定理是不是勾股定理。在普路塔克之后,陆续有人提到这件事,而且很肯定的说这个几何定理就是勾股定理。到公元五世纪,普罗克勒斯在欧几里德的名著《几何原本》中勾股定理的证明旁边写了一个注记:
如果我们听听那些喜欢说古代历史的人,他们把这个定理归于毕达哥拉斯,并且说他杀了一头公牛来庆祝。对我来说,虽然我欣赏那个第一个观察到这个定理的人,我更叹服《原本》的作者。不光是因为他给出了清晰明确的证明,而且还因为他用无可置疑的方法在第六篇中证明了一个更一般的命题。
这已经是毕达哥拉斯死了千年之后的事情了。再后来有人说毕达哥拉斯杀了100头牛来庆祝。甚至有人据此称勾股定理为“百牛定理”。
那么上面的故事到底有多少可信度呢?让我们来看看普路塔克之前的人是怎么说毕达哥拉斯的。奥维德是公元前43年出生的古罗马诗人,他著名的作品有大家熟悉的《变形记》。奥维德记录了毕达哥拉斯说过的这样一句话“人类只要屠杀动物,就会屠杀自己。播下痛苦和杀戮的种子,是收获不到爱和快乐的。”
奥维德的记录如果是可信的话,普路塔克的记录肯定就是错误的,因为毕达哥拉斯不可能去杀牛。毕达哥拉斯的道德规范禁止一切杀生,禁止粗暴的流血,动物祭祀更是绝对不允许的事情。一直到十九世纪末,在西方,不吃肉的人还被称为“毕达哥拉斯的信徒。”
那么科学家们又是怎么说的呢?生活在普路塔克之前,毕达哥拉斯之后有很多著名科学家,例如亚里斯多德,阿基米德,欧几里德,他们的著作里面没有任何地方提到毕达哥拉斯跟勾股定理有任何关系。到公元五世纪,从普罗克勒斯的话可以看出,他虽然认为有可能是毕达哥拉斯先发现了勾股定理,但并不认为是毕达哥拉斯先证明了勾股定理。
现在有据可查的最早的证明是欧几里德在《几何原本》中给出的。那么有没有可能在欧几里德之前,这个证明就广为人知了呢?答案是几乎不可能。因为勾股定理的证明依赖《几何原本》中的第五公设。这个第五公设也就是平行公理,相当于说在平面上,过直线外一点,有且仅有一条不与该直线相交的直线。这个第五公设在当时是饱受攻击的,也就是说绝大多数人认为这个公设不需要先假设成立,而是可以被证明出来。这个局面一直持续到19世纪,高斯年轻时代曾感叹自己并不比欧几里德多了解第五公设。有趣的是由勾股定理出发,可以很简单的推导出第五公设成立。这样,如果勾股定理真的深入人心的话,大家就不可能去纠缠第五公设是否成立了。
勾股定理早已为中国人所知,在中国古代大约是战国时期西汉的数学著作 《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。这就是中国著名的勾股定理。
实际上,在更早期的人类活动中,人们就已经认识到这一定理的某些特例。除我国在公元前一千多年前发现勾股定理外,据说古埃及人也曾利用“勾三股四弦五”的法则来确定直角。但是,这一传说引起过许多数学史家的怀疑。比如说,美国的数学史家M·克莱因教授曾经指出:“我们也不知道埃及人是否认识到毕达哥拉斯定理。我们知道他们有拉绳人(测量员),但所传他们在绳上打结,把全长分成长度为3、4、5的三段,然后用来形成直角三角形之说,则从未在任何文件上得证实。”
不过,考古学家们发现了几块大约完成于公元前两千年左右的古巴比伦的泥板书,据专家们考证,其中一块上面刻有如下问题:“一根长度为30个单位的棍子直立在墙上,当其上端滑下6个单位时,请问其下端离开墙角有多远?”
这是一个三边为为3:4:5三角形的特殊例子;专家们还发现,在另一块泥板上面刻着一个奇特的数表,表中共刻有四列十五行数字,这是一个勾股数表:最右边一列为从1到15的序号,而左边三列则分别是股、勾、弦的数值,一共记载着15组勾股数。这说明,勾股定理实际上早已进入了人类知识的宝库。
无论是古埃及人、古巴比伦人还是我们中国人谁最先发现了勾股定理,我们的先人在不同的时期、不同的地点发现的这同一性质,显然不仅仅是哪一个民族的私有财产而是我们全人类的共同财富。值得一提的是:在发现这一共同性质后的收获却是不完全相同的。
毕达哥拉斯是一个古希腊人的名宇。生于公元前六世纪的毕达哥拉斯,早年曾游历埃及、巴比伦(另一种说法是到过印度)等地,后来移居意大利半岛南部的克罗托内,并在那里组织了一个集政治、宗教、数学于一体的秘密团体──毕达哥拉斯学派,这个学派非常重视数学,企图用数来解释一切。他们宣称,数是宇宙万物的本原,研究数学的目的并不在于实用,而是为了探索自然的奥秘。他们对数学看法的一个重大贡献是有意识地承认并强调;数学上的东西如数和图形是思维的抽象,同实际事物或实际形象是截然不同的。有些原始文明社会中的人(如埃及人和巴比伦人)也知道把数脱离实物来思考,但他们对这种思考的抽象性质所达到的自觉认识程度,与毕达哥拉斯学派相比,是有相当差距的。而且在希腊人之前,几何思想是离不开实物的。例如,埃及人认为,直线就是拉紧的绳或田地的一条边;而矩形则是田地的边界。这个学派还有一个特点,就是将算术和几何紧密联系起来。
正因为如此,毕达哥拉斯学派在他们的探索中,发现了用三个整数的勾股数组表示直角三角形边长的公式,不过这法则并不能把所有的整勾股数组表示出来,
也正是由于上述原因,这个学派通过对整勾股数的寻找和研究,发现了所谓的“不可通约量” ──例如,等腰直角三角形斜边与一直角边之比即正方形对角线与其一边之比不能用整数之比表达。为此,他们把那些能用整数之比表达的比称做“可公度比”,意即相比两量可用公共度量单位量尽,而把不能这样表达的比称做“不可公度比”。像2的算术平方根与l的比便是不可公度比。至于2的算术平方根与1不能公度的证明也是毕达哥拉斯学派给出的。
这个证明指出:若设等腰直角三角形斜边能与一直角边公度,那么,同一个数将既是奇数又是偶数。
《欧几里得原本》中毕达哥拉斯定理的证明
关于对毕达哥拉斯定理的证明,现在人类保存下来的最早的文字资料是欧几里得所著的《几何原本》第一卷中的命题四十七:“直角三角形斜边上的正方形等于两直角边上的两个正方形之和”。其证明是用面积来进行的。如下图
《几何原本》第一卷中的命题四十七图
△ABD ≌△FBC,矩形BL=2△ABD,
正方形GB=2△凸FBC。
于是,矩形BL=正方形GB。
同样有,矩形CL=正方形AK。
所以,正方形GB+正方形AK=正方形BE。
毕达哥拉斯学派对勾股定理的研究及其收获由此可见一般。实际上,毕达哥拉斯学派关心得更多的是数学问题本身的研究;以毕达哥拉斯学派为代表的古希腊数学是以空间形式为主要研究对象,以逻辑上的演绎推理为主要的理论形式。而毕达哥拉斯定理的发现(关于可公度比与不可公度比的研究、讨论),实际上导致了无理数的发现,尽管毕达哥拉斯学派不愿意接受这样的数,并因此造成了数学史上所谓的第一次数学危机,但是毕达哥拉斯学派的探索仍然是功不可没的。
古巴比伦汉谟拉比时期的勾股定理
汉谟拉比是公元前十八世纪的古巴比伦国王。他颁布的著名的《汉谟拉比法典》,被认为是世界上最早的一部比较系统的法典。古巴比伦是四大文明古国之一,其地理位置是现在伊拉克地区。那个时候的中国正处在大禹创立的夏朝。
勾股定理,说的是直角三角形两条直角边的平方之和等于斜边的平方。在成书于公元前一世纪左右的《周髀算经》里有“句广三,股修四,径隅五”。这里的“句”念作“勾”,指的是直角三角形的短边,后来写法也演变成现在的“勾”。“股”指的是直角三角形的长边。古人用直角三角形来测量,将长的直角边树立起来以后,像腿一样。所以叫做“股”,也就是腿的意思。“径”指的是斜边。西方长期以来认为是公元前六世纪的古希腊数学家毕达哥拉斯最先发现这个定理,所以称它为毕达哥拉斯定理。
其实这个定理可能在汉谟拉比时期就已经有了。耶鲁大学收藏了很多公元前2000年至公元前1600年的古巴比伦泥板。其中有一块编号为YBC7289的泥板可能完全改写勾股定理的历史。
YBC7289泥板:比毕达哥拉斯早一千年的毕达哥拉斯定理
这块泥板上画有一个正方形和这个正方形的两条对角线。在这个正方形的一条边上写着一个数字30,在一条对角线上写着1,24,51,10,紧靠这个数字的下方写着42,25,35。
古巴比伦人用的60进位制,也就是说满了60才向左进一位。所以
“1,24,51,10”翻译成十进制就是1+24/60+51/3600+10/216000=30547/21600,
“42,25,35” 翻译成十进制是42+25/60+35/3600=30547/720。
仔细观察这三个数字可以发现 30乘以30547/21600恰好是30547/720。也就是说这副图其实是一道数学题。那么30547/21600是多少呢?简单的计算可知大约是1.41421296…, 跟2的平方根(大约是1.41421356…)相差只有0.00004%。所以这幅图的含义就是将正方形的边长乘上2的平方根就是对角线的长度了。
后来有专家发现古巴比伦人记号混乱,那个30有可能是小数部分,也就是
30/60=1/2。如果是这样的话,那么对角线长附近的“42,25,35”指的实际上是
42/60+25/3600+35/216000=30547/43200。也就是说这副图的含义是边长为1/2的正方形对角线长为2的平方根的一半。
不管是那种情况,至少可以说明古巴比伦人知道等腰直角三角形的勾股定理。因为单凭测量是不可能达到99.99996%的精确率的。他们一定是知道斜边长平方是直角边长平方的2倍,然后通过数学计算得到的。而且那个图本身其实就是一个证明,是我国三国时期的数学家赵爽用来证明勾股定理的图的特例。
仅仅是这块泥板还不足以证明古巴比伦人知道一般形式的勾股定理。但是人们又发现了其他的泥板。在英国博物馆保存的一块相同时期的泥板上有这样的记载:
长是4,对角线是5。那么宽是多少?
没人知道。
4乘4是16。
5乘5是25。
你从25里面拿掉16,剩下的是9。
几乘几是9呀?
3乘3是9。
3就是宽。
这段文字说明古巴比伦人知道当直角三角形的斜边是5,一条直角边是4的时候,另外一条直角边一定是3。
古巴比伦人还知道其他的勾股数组的例子吗?当然! 在美国哥伦比亚大学收藏的一块编号为PLIMPTON 322的泥板上记录了很多例子。这块泥板上总共有15行符号,分成5列。其中第四列相当于我们的“编号”两个字,第五列从第一行到最后一行依次是从1到15这15个数字。所以说真正有意义的其实只有前3列。第三列是斜边长,第二列是短的直角边长。最令人费解的是第一列,这一列的数字从第一行的0.9834…逐渐减少到最后一行的0.38716…。关于这第一列的含义,长期以来争论不休。美国威斯康星大学巴克教授于1980年写了一篇脍炙人口的文章《夏洛克.福尔摩斯在巴比伦》。这篇文章发表在《美国数学月刊上》。巴克教授在这篇文章里从大侦探福尔摩斯的角度出发来研究这些数字。其结论令人吃惊不已。
勾股定理《周髀算经》的证明
《周髀算经》为算经十书之一。约成书于公元前二世纪,原名《周髀》,它是中国最古老的天文学著作,主要阐明当时的盖天说和四分历法。
唐初规定它为国子监明算科的教材之一,故改名《周髀算经》。
首先,《周髀算经》中明确记载了勾股定理的公式:“若求邪至日者,以日下为句,日高为股,句股各自乘,并而开方除之,得邪至日”(《周髀算经》上卷二)
而勾股定理的证明呢,就在《周髀算经》上卷一[5]
昔者周公问于商高曰:“窃闻乎大夫善数也,请问昔者包牺立周天历度——夫天可不阶而升,地不可得尺寸而度,请问数安从出?”
商高曰:“数之法出于圆方,圆出于方,方出于矩,矩出于九九八十一。故折矩,以为句广三,股修四,径隅五。既方之,外半其一矩,环而共盘,得成三四五。两矩共长二十有五,是谓积矩。故禹之所以治天下者,此数之所生也。”
周公对古代伏羲(包牺)构造周天历度的事迹感到不可思议(天不可阶而升,地不可得尺寸而度),就请教商高数学知识从何而来。于是商高以勾股定理的证明为例,解释数学知识的由来。
勾股定理《周髀算经》的证明
《周髀算经》证明步骤
“数之法出于圆方,圆出于方,方出于矩,矩出于九九八十一。”:解释发展脉络──数之法出于圆(圆周率三)方(四方),圆出于方(圆形面积=外接正方形×圆周率÷4),方出于矩(正方形源自两边相等的矩),矩出于九九八十一(长乘宽面积计算依自九九乘法表)。
“故折矩①,以为勾广三,股修四,径隅五。”:开始做图──选择一个勾三(圆周率三)、股四(四方) 的矩,矩的两条边终点的连线应为5(径隅五)。
“②既方之,外半其一矩,环而共盘,得成三四五。”:这就是关键的证明过程──以矩的两条边画正方形(勾方、股方),根据矩的弦外面再画一个矩(曲尺,实际上用作直角三角),将“外半其一矩”得到的三角形剪下环绕复制形成一个大正方形,可看到其中有边长三勾方、边长四股方、边长五弦方三个正方形。
“两矩共长③二十有五,是谓积矩。”:此为验算──勾方、股方的面积之和,与弦方的面积二十五相等──从图形上来看,大正方形减去四个三角形面积后为弦方,再是大正方形减去右上、左下两个长方形面积后为勾方股方之和。因三角形为长方形面积的一半,可推出四个三角形面积等于右上、左下两个长方形面积,所以勾方+股方=弦方。
注意:
① 矩,又称曲尺,L型的木匠工具,由长短两根木条组成的直角。古代“矩”指L型曲尺,“矩形”才是“矩”衍生的长方形。
② “既方之,外半其一矩”此句有争议。清代四库全书版定为“既方其外半之一矩”,而之前版本多为“既方之外半其一矩”。经陈良佐、李国伟、李继闵、曲安京等学者研究,“既方之,外半其一矩”更符合逻辑。
③ 长指的是面积。古代对不同维度的量纲比较,并没有发明新的术语,而统称“长”。赵爽注称:“两矩者, 句股各自乘之实。共长者,并实之数。
由于年代久远,周公弦图失传,传世版本只印了赵爽弦图(造纸术在汉代才发明)。所以某些学者误以为商高没有证明(只是说了一段莫名其妙的话),后来赵爽才给出证明。
赵爽关于勾股定理的证明
现存数学典籍中最早给出勾股定理证明的是赵爽的《周髀算经注》。
赵爽又名婴,字君卿,三国时吴国人。由于史书上没有他的传记,所以他的生卒年代和生平事迹已不可详考了。从他自己所说“负薪余日、聊观《周髀》”的话来看,可能是个平民数学家.他在读了《周髀算经》后,深为此书的数学内容所折服,又恐怕后人不能彻底理解其中的深奥道理,于是就动手对它作了全面的注释和阐述。其中给出的《勾股圆方图》和《勾股圆方图注》,便是对勾股定理的一个严格而又巧妙的证明。
赵爽弦图
青朱出入图
三角形为直角三角形,以勾a为边的正方形为朱方,以股b为边的正方形为青方。以盈补虚,将朱方、青方并成弦方。
依其面积关系有A的平方+B的平方=C的平方。
由于朱方、青方各有一部分在玄方内,那一部分就不动了。
以勾为边的的正方形为朱方,以股为边的正方形为青方。以盈补虚,只要把图中朱方(A的平方)的I移至I′,青方的II移至II′,III移至III′,则刚好拼好一个以弦为边长的正方形(C……2 ).由此便可证得A的平方+B的平方=C的平方。
勾股定理的其他证明方法
勾股定理有许多证明的方法,其证明的方法可能是数学众多定理中最多的。
关于勾股定理证明,上至美国总统,下至英国商人,甚至意大利画家达·芬奇对勾股定理也曾进行验证。
ElishaScott Loomis(路明思或译为卢米斯)在他1940年发表的《毕达哥拉斯定理》(PythagoreanProposition)一书的第二版中就收集了这个定理的367种证明方法,并对它们进行了分类,但多是用面积分割型的方法。
印度数学家婆什迦罗(Bhaskara,活跃于1150年前后)对勾股定理给出一种奇妙的证明,也是一种分割型的证明。
上图中,显然有:AC的平方等于AO×AB;CB的平方等于BO×AB;两式相加即得证。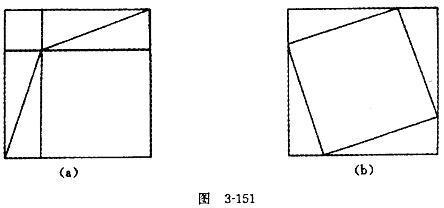
 爱华网
爱华网