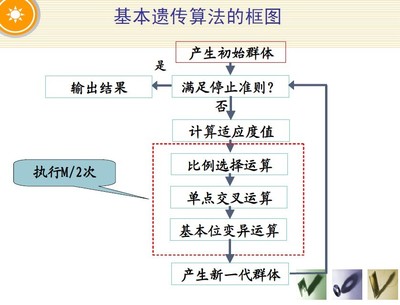
①遗传算法不是对变量直接操作,而是对其编码进行操作:
② 它是从一组点出发进行搜索,而不是从单个点开始;
③ 它不需要导数等信息;
④它是一种随机搜索算法。
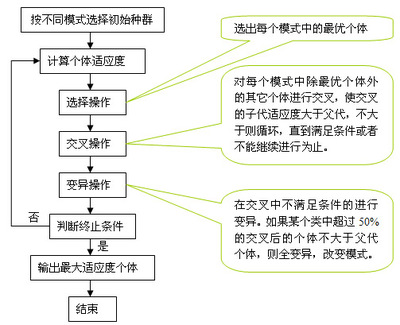
遗传算法的主要操作有:复制、交叉、变异。复制体现了“适者生存,不适者淘汰”的自然选择机制。交叉操作使得后代能够继承父代的优良特性。变异操作在增加种群多样性方面具有重要作用。
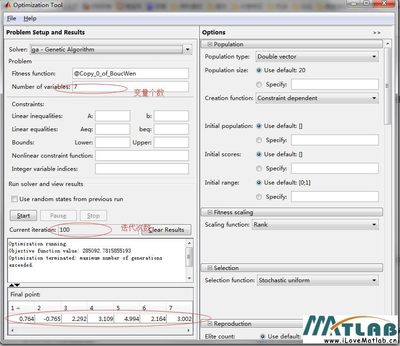
遗传算法的应用过程主要包括:编码、构造初始种群、设计适应度函数、确定遗传算法结构、选择遗传算子、确定遗传算法的控制参数.
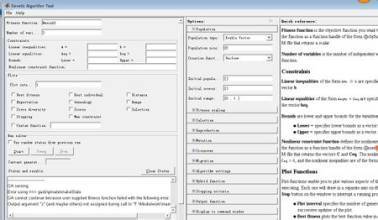
下面是Matlab遗传算法工具箱函数的说明和实例说明:
核心函数:
(1)function[pop]=initializega(num,bounds,eevalFN,eevalOps,options)--初始种群的生成函数
【输出参数】
pop--生成的初始种群
【输入参数】
num--种群中的个体数目
bounds--代表变量的上下界的矩阵
eevalFN--适应度函数
eevalOps--传递给适应度函数的参数
options--选择编码形式(浮点编码或是二进制编码)[precisionF_or_B],如
precision--变量进行二进制编码时指定的精度
F_or_B--为1时选择浮点编码,否则为二进制编码,由precision指定精度)
(2)function [x,endPop,bPop,traceInfo] =ga(bounds,evalFN,evalOps,startPop,opts,...
termFN,termOps,selectFN,selectOps,xOverFNs,xOverOps,mutFNs,mutOps)--遗传算法函数
【输出参数】
x--求得的最优解
endPop--最终得到的种群
bPop--最优种群的一个搜索轨迹
【输入参数】
bounds--代表变量上下界的矩阵
evalFN--适应度函数
evalOps--传递给适应度函数的参数
startPop-初始种群
opts[epsilon prob_opsdisplay]--opts(1:2)等同于initializega的options参数,第三个参数控制是否输出,一般为0。如[1e-61 0]
termFN--终止函数的名称,如['maxGenTerm']
termOps--传递个终止函数的参数,如[100]
selectFN--选择函数的名称,如['normGeomSelect']
selectOps--传递个选择函数的参数,如[0.08]
xOverFNs--交叉函数名称表,以空格分开,如['arithXoverheuristicXover simpleXover']
xOverOps--传递给交叉函数的参数表,如[20;2 3;2 0]
mutFNs--变异函数表,如['boundaryMutationmultiNonUnifMutation nonUnifMutationunifMutation']
mutOps--传递给交叉函数的参数表,如[40 0;6 100 3;4 100 3;4 0 0]
【注意】matlab工具箱函数必须放在工作目录下
遗传算法实例1
【问题】求f(x)=x+10*sin(5x)+7*cos(4x)的最大值,其中0<=x<=9
【分析】选择二进制编码,种群中的个体数目为10,二进制编码长度为20,交叉概率为0.95,变异概率为0.08
【程序清单】
%编写目标函数
function[sol,eval]=fitness(sol,options)
x=sol(1);
eval=x+10*sin(5*x)+7*cos(4*x);
%把上述函数存储为fitness.m文件并放在工作目录下
initPop=initializega(10,[09],'fitness');%生成初始种群,大小为10
[x endPop,bPop,trace]=ga([09],'fitness',[],initPop,[1e-6 11],'maxGenTerm',25,'normGeomSelect',...
[0.08],['arithXover'],[2],'nonUnifMutation',[2 253]) %次遗传迭代
运算结果为:x=
7.856224.8553(当x为7.8562时,f(x)取最大值24.8553)
注:遗传算法一般用来取得近似最优解,而不是最优解。
遗传算法实例2
【问题】在-5<=Xi<=5,i=1,2区间内,求解
f(x1,x2)=-20*exp(-0.2*sqrt(0.5*(x1.^2+x2.^2)))-exp(0.5*(cos(2*pi*x1)+cos(2*pi*x2--)))+22.71282的最小值。
【分析】种群大小10,最大代数1000,变异率0.1,交叉率0.3
【程序清单】
%源函数的matlab代码
function[eval]=f(sol)
numv=size(sol,2);
x=sol(1:numv);
eval=-20*exp(-0.2*sqrt(sum(x.^2)/numv)))-exp(sum(cos(2*pi*x))/numv)+22.71282;
%适应度函数的matlab代码
function[sol,eval]=fitness(sol,options)
numv=size(sol,2)-1;
x=sol(1:numv);
eval=f(x);
eval=-eval;
%遗传算法的matlab代码
bounds=ones(2,1)*[-5 5];
[p,endPop,bestSols,trace]=ga(bounds,'fitness')
注:前两个文件存储为m文件并放在工作目录下,运行结果为
p=
0.0000 -0.00000.0055
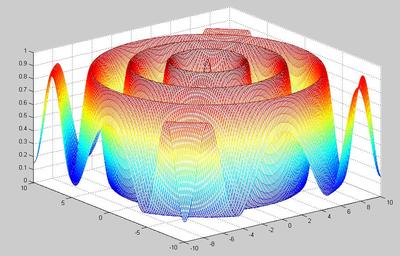
大家可以直接绘出f(x)的图形来大概看看f(x)的最值是多少,也可是使用优化函数来验证。matlab命令行执行命令:
fplot('x+10*sin(5*x)+7*cos(4*x)',[0,9])
evalops是传递给适应度函数的参数,opts是二进制编码的精度,termops是选择maxGenTerm结束函数时传递个maxGenTerm的参数,即遗传代数。xoverops是传递给交叉函数的参数。mutops是传递给变异函数的参数。
 爱华网
爱华网